|
|
| (5 intermediate revisions by 4 users not shown) |
| Line 1: |
Line 1: |
| | + | {{TEX|done}} |
| | A plane curve whose equation in polar coordinates has the form | | A plane curve whose equation in polar coordinates has the form |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085650/s0856501.png" /></td> </tr></table>
| + | $$\rho^m=a^m\cos m\phi.$$ |
| | | | |
| − | When <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085650/s0856502.png" /> is rational, this is an [[Algebraic curve|algebraic curve]]. In particular, when <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085650/s0856503.png" /> it is a circle, when <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085650/s0856504.png" /> — an equilateral hyperbola, when <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085650/s0856505.png" /> — a [[Cardioid|cardioid]], and when <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085650/s0856506.png" /> — a parabola. | + | When $m$ is rational, this is an [[algebraic curve]]. In particular, when $m=1$ it is a circle, when $m=-1$ — an equilateral hyperbola, when $m=1/2$ — a [[cardioid]], and when $m=-1/2$ — a parabola. |
| | | | |
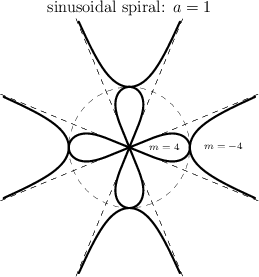
| − | For general <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085650/s0856507.png" /> the sinusoidal spiral passes through the pole, and is entirely contained within a circle of radius <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085650/s0856508.png" />. When <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085650/s0856509.png" /> is negative, the radius vector of the curve can take arbitrarily large values and the curve does not pass through the pole. The sinusoidal spiral is symmetric with respect to the polar axis, and when <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085650/s08565010.png" /> is rational (where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085650/s08565011.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085650/s08565012.png" /> are relatively prime numbers), it has <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085650/s08565013.png" /> axes of symmetry passing through the pole. When <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085650/s08565014.png" /> is a positive integer, the radius vector of the curve is a periodic function of period <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085650/s08565015.png" />. As <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085650/s08565016.png" /> goes from 0 to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085650/s08565017.png" />, the curve consists of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085650/s08565018.png" /> branches, each contained in an angle of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085650/s08565019.png" />. In this case the pole is a multiple point (see Fig.). When <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085650/s08565020.png" /> is a positive rational number, the curve consists of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085650/s08565021.png" /> intersecting branches. When <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085650/s08565022.png" /> is a negative integer, the curve consists of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085650/s08565023.png" /> infinite branches, which can be obtained by inverting the spiral with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085650/s08565024.png" />. | + | For general $m>0$ the sinusoidal spiral passes through the pole, and is entirely contained within a circle of radius $a$. When $m$ is negative, the radius vector of the curve can take arbitrarily large values and the curve does not pass through the pole. The sinusoidal spiral is symmetric with respect to the polar axis, and when $m=p/q$ is rational (where $p$ and $q$ are relatively prime numbers), it has $p$ axes of symmetry passing through the pole. When $m$ is a positive integer, the radius vector of the curve is a periodic function of period $2\pi/m$. As $\phi$ goes from 0 to $2\pi$, the curve consists of $m$ branches, each contained in an angle of $\pi/m$. In this case the pole is a multiple point (see Fig.). When $m=p/q$ is a positive rational number, the curve consists of $p$ intersecting branches. When $m$ is a negative integer, the curve consists of $|m|$ infinite branches, which can be obtained by inverting the spiral with $m'=-m$. |
| − | | + | {{:Sinusoidal spiral/Fig1}} |
| − | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/s085650a.gif" />
| |
| − | | |
| − | Figure: s085650a
| |
| | | | |
| | ====References==== | | ====References==== |
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> A.A. Savelov, "Planar curves" , Moscow (1960) (In Russian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> J.D. Lawrence, "A catalog of special plane curves" , Dover, reprint (1972)</TD></TR></table> | + | <table> |
| − | | + | <TR><TD valign="top">[1]</TD> <TD valign="top"> A.A. Savelov, "Planar curves", Moscow (1960) (In Russian)</TD></TR> |
| − | | + | <TR><TD valign="top">[2]</TD> <TD valign="top"> J.D. Lawrence, "A catalog of special plane curves", Dover (1972) {{ISBN|0-486-60288-5}} {{ZBL|0257.50002}}</TD></TR> |
| | + | <TR><TD valign="top">[a1]</TD> <TD valign="top"> E.H. Lockwood, "A book of curves" , Cambridge Univ. Press (1967)</TD></TR> |
| | + | </table> |
| | | | |
| − | ====Comments====
| |
| | | | |
| − | | + | {{OldImage}} |
| − | ====References====
| |
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> E.H. Lockwood, "A book of curves" , Cambridge Univ. Press (1967)</TD></TR></table>
| |
A plane curve whose equation in polar coordinates has the form
$$\rho^m=a^m\cos m\phi.$$
When $m$ is rational, this is an algebraic curve. In particular, when $m=1$ it is a circle, when $m=-1$ — an equilateral hyperbola, when $m=1/2$ — a cardioid, and when $m=-1/2$ — a parabola.
For general $m>0$ the sinusoidal spiral passes through the pole, and is entirely contained within a circle of radius $a$. When $m$ is negative, the radius vector of the curve can take arbitrarily large values and the curve does not pass through the pole. The sinusoidal spiral is symmetric with respect to the polar axis, and when $m=p/q$ is rational (where $p$ and $q$ are relatively prime numbers), it has $p$ axes of symmetry passing through the pole. When $m$ is a positive integer, the radius vector of the curve is a periodic function of period $2\pi/m$. As $\phi$ goes from 0 to $2\pi$, the curve consists of $m$ branches, each contained in an angle of $\pi/m$. In this case the pole is a multiple point (see Fig.). When $m=p/q$ is a positive rational number, the curve consists of $p$ intersecting branches. When $m$ is a negative integer, the curve consists of $|m|$ infinite branches, which can be obtained by inverting the spiral with $m'=-m$.
References
| [1] | A.A. Savelov, "Planar curves", Moscow (1960) (In Russian) |
| [2] | J.D. Lawrence, "A catalog of special plane curves", Dover (1972) ISBN 0-486-60288-5 Zbl 0257.50002 |
| [a1] | E.H. Lockwood, "A book of curves" , Cambridge Univ. Press (1967) |
🛠️ This page contains images that should be replaced by better images in the SVG file format. 🛠️
