Cardioid
From Encyclopedia of Mathematics
A plane algebraic curve of order four which is described by a point $M$ of a circle of radius $r$ rolling on a circle with the same radius $r$; an epicycloid with modulus $m=1$. The equation of the cardioid in polar coordinates is:
$$\rho=2r(1-\cos\phi),$$
In Cartesian coordinates it is:
$$(x^2+y^2+2rx)^2=4r^2(x^2+y^2).$$
The arc length from the cusp is:
$$l=16r\sin^2\frac\phi4.$$
The radius of curvature is:
$$r_k=\frac{8r}{3}\sin\frac\phi2.$$
The area bounded by the curve equals $S=6\pi r^2$. The length of the curve is $16r$. The cardioid is a conchoid of the circle, a special case of a Pascal limaçon and a sinusoidal spiral.
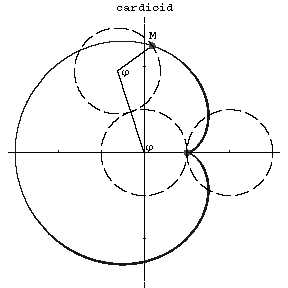
Figure: c020390a
References
| [1] | A.A. Savelov, "Planar curves" , Moscow (1960) (In Russian) |
| [a1] | J.D. Lawrence, "A catalog of special plane curves" , Dover, reprint (1972) |
🛠️ This page contains images that should be replaced by better images in the SVG file format. 🛠️
How to Cite This Entry:
Cardioid. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Cardioid&oldid=53339
Cardioid. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Cardioid&oldid=53339
This article was adapted from an original article by D.D. Sokolov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article