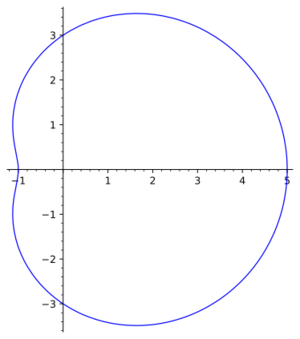
Pascal limaçon
A plane algebraic curve of order 4; a conchoid of a circle of diameter $a$ (see Fig.).
The equation in rectangular coordinates is
$$(x^2+y^2-ax)^2=l^2(x^2+y^2);$$
in polar coordinates it is
$$\rho=a\cos\phi+l.$$
The coordinate origin is a double point, which is an isolated point for $a<l$, a node for $a>l$, and a cusp for $a=l$ (in this case Pascal's limaçon is a cardioid). The arc length can be expressed by an elliptic integral of the second kind. The area bounded by Pascal's limaçon is
$$S=\frac{\pi a^2}{2}+\pi l^2;$$
for $a>l$ the area of the inner leaf must be counted double in calculating according to this formula. The Pascal limaçon is a special case of a Descartes oval; it is an epitrochoid.
The limaçon is named after Étienne Pascal, who first treated it in the first half of the 17th century.
References
| [1] | A.A. Savelov, "Planar curves" , Moscow (1960) (In Russian) |
Comments
Étienne Pascal (1588–1651) was the father of Blaise Pascal.
References
| [a1] | M. Berger, "Geometry" , 1–2 , Springer (1987) (Translated from French) |
| [a2] | F. Gomes Teixeira, "Traité des courbes" , 1–3 , Chelsea, reprint (1971) |
| [a3] | J.D. Lawrence, "A catalog of special plane curves" , Dover (1972) pp. 113–118; ISBN 0-486-60288-5 Zbl 0257.50002 |
Pascal limaçon. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Pascal_lima%C3%A7on&oldid=53879