|
|
| (2 intermediate revisions by 2 users not shown) |
| Line 1: |
Line 1: |
| − | A Howell design of side <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110330/h1103301.png" /> and order <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110330/h1103302.png" />, or more briefly an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110330/h1103303.png" />, is an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110330/h1103304.png" />-array in which each cell is either empty or contains an unordered pair of distinct elements from some <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110330/h1103305.png" />-set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110330/h1103306.png" /> such that:
| + | <!-- |
| | + | h1103301.png |
| | + | $#A+1 = 78 n = 2 |
| | + | $#C+1 = 78 : ~/encyclopedia/old_files/data/H110/H.1100330 Howell design |
| | + | Automatically converted into TeX, above some diagnostics. |
| | + | Please remove this comment and the {{TEX|auto}} line below, |
| | + | if TeX found to be correct. |
| | + | --> |
| | | | |
| − | 1) every element of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110330/h1103307.png" /> occurs in precisely one cell of each row and each column;
| + | {{TEX|auto}} |
| | + | {{TEX|done}} |
| | | | |
| − | 2) every unordered pair of elements from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110330/h1103308.png" /> is in at most one cell of the array. It follows immediately from the definition of an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110330/h1103309.png" /> that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110330/h11033010.png" />. An example of a Howell design is the following <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110330/h11033011.png" />:''''''<table border="0" cellpadding="0" cellspacing="0" style="background-color:black;"> <tr><td> <table border="0" cellspacing="1" cellpadding="4" style="background-color:black;"> <tbody> <tr> <td colname="1" style="background-color:white;" colspan="1"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110330/h11033012.png" /> 0</td> <td colname="2" style="background-color:white;" colspan="1"></td> <td colname="3" style="background-color:white;" colspan="1">1 3</td> <td colname="4" style="background-color:white;" colspan="1"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110330/h11033013.png" /> 2</td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1"></td> <td colname="4" style="background-color:white;" colspan="1"></td> <td colname="3" style="background-color:white;" colspan="1"></td> <td colname="2" style="background-color:white;" colspan="1"></td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1">2 3</td> <td colname="2" style="background-color:white;" colspan="1"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110330/h11033014.png" /> 1</td> <td colname="3" style="background-color:white;" colspan="1"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110330/h11033015.png" /> 0</td> <td colname="4" style="background-color:white;" colspan="1"></td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1"></td> <td colname="4" style="background-color:white;" colspan="1"></td> <td colname="3" style="background-color:white;" colspan="1"></td> <td colname="2" style="background-color:white;" colspan="1"></td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1"></td> <td colname="2" style="background-color:white;" colspan="1"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110330/h11033016.png" /> 3</td> <td colname="3" style="background-color:white;" colspan="1"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110330/h11033017.png" /> 2</td> <td colname="4" style="background-color:white;" colspan="1">0 1</td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1"></td> <td colname="4" style="background-color:white;" colspan="1"></td> <td colname="3" style="background-color:white;" colspan="1"></td> <td colname="2" style="background-color:white;" colspan="1"></td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110330/h11033018.png" /> 1</td> <td colname="2" style="background-color:white;" colspan="1">0 2</td> <td colname="3" style="background-color:white;" colspan="1"></td> <td colname="4" style="background-color:white;" colspan="1"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110330/h11033019.png" /> 3</td> </tr> </tbody> </table> | + | A Howell design of side $ s $ |
| | + | and order $ 2n $, |
| | + | or more briefly an $ H ( s,2n ) $, |
| | + | is an $ ( s \times s ) $- |
| | + | array in which each cell is either empty or contains an unordered pair of distinct elements from some $ 2n $- |
| | + | set $ V $ |
| | + | such that: |
| | + | |
| | + | 1) every element of $ V $ |
| | + | occurs in precisely one cell of each row and each column; |
| | + | |
| | + | 2) every unordered pair of elements from $ V $ |
| | + | is in at most one cell of the array. It follows immediately from the definition of an $ H ( s,2n ) $ |
| | + | that $ n \leq s \leq 2n - 1 $. |
| | + | An example of a Howell design is the following $ H ( 4,6 ) $: |
| | + | |
| | + | <table border="0" cellpadding="0" cellspacing="0" style="background-color:black;"> <tr><td> <table border="0" cellspacing="1" cellpadding="4" style="background-color:black;"> <tbody> <tr> <td colname="1" style="background-color:white;" colspan="1"> $ \alpha $ |
| | + | 0</td> <td colname="2" style="background-color:white;" colspan="1"></td> <td colname="3" style="background-color:white;" colspan="1">1 3</td> <td colname="4" style="background-color:white;" colspan="1"> $ \infty $ |
| | + | 2</td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1"></td> <td colname="4" style="background-color:white;" colspan="1"></td> <td colname="3" style="background-color:white;" colspan="1"></td> <td colname="2" style="background-color:white;" colspan="1"></td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1">2 3</td> <td colname="2" style="background-color:white;" colspan="1"> $ \alpha $ |
| | + | 1</td> <td colname="3" style="background-color:white;" colspan="1"> $ \infty $ |
| | + | 0</td> <td colname="4" style="background-color:white;" colspan="1"></td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1"></td> <td colname="4" style="background-color:white;" colspan="1"></td> <td colname="3" style="background-color:white;" colspan="1"></td> <td colname="2" style="background-color:white;" colspan="1"></td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1"></td> <td colname="2" style="background-color:white;" colspan="1"> $ \infty $ |
| | + | 3</td> <td colname="3" style="background-color:white;" colspan="1"> $ \alpha $ |
| | + | 2</td> <td colname="4" style="background-color:white;" colspan="1">0 1</td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1"></td> <td colname="4" style="background-color:white;" colspan="1"></td> <td colname="3" style="background-color:white;" colspan="1"></td> <td colname="2" style="background-color:white;" colspan="1"></td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1"> $ \infty $ |
| | + | 1</td> <td colname="2" style="background-color:white;" colspan="1">0 2</td> <td colname="3" style="background-color:white;" colspan="1"></td> <td colname="4" style="background-color:white;" colspan="1"> $ \alpha $ |
| | + | 3</td> </tr> </tbody> </table> |
| | | | |
| | </td></tr> </table> | | </td></tr> </table> |
| | | | |
| − | An <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110330/h11033020.png" /> is also called a [[Room square|Room square]] of side <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110330/h11033021.png" />. At the other extreme, the existence of a pair of mutually [[Orthogonal Latin squares|orthogonal Latin squares]] implies the existence of an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110330/h11033022.png" />. The existence of Howell designs has been completely determined [[#References|[a1]]], [[#References|[a5]]]: Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110330/h11033023.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110330/h11033024.png" /> be positive integers such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110330/h11033025.png" />. There exists an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110330/h11033026.png" /> if and only if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110330/h11033027.png" /> or <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110330/h11033028.png" />. The proof uses a variety of direct and recursive constructions. | + | An $ H ( 2n - 1,2n ) $ |
| | + | is also called a [[Room square|Room square]] of side $ 2n - 1 $. |
| | + | At the other extreme, the existence of a pair of mutually [[Orthogonal Latin squares|orthogonal Latin squares]] implies the existence of an $ H ( n,2n ) $. |
| | + | The existence of Howell designs has been completely determined [[#References|[a1]]], [[#References|[a5]]]: Let $ s $ |
| | + | and $ n $ |
| | + | be positive integers such that $ 0 \leq n \leq s \leq 2n - 1 $. |
| | + | There exists an $ H ( s,2n ) $ |
| | + | if and only if $ ( s,2n ) \neq ( 2,4 ) , ( 3,4 ) , ( 5,6 ) $ |
| | + | or $ ( 5,8 ) $. |
| | + | The proof uses a variety of direct and recursive constructions. |
| | | | |
| − | An <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110330/h11033029.png" /> is an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110330/h11033030.png" /> in which there is a subset <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110330/h11033031.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110330/h11033032.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110330/h11033033.png" />, such that no pair of elements from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110330/h11033034.png" /> appears in the design. <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110330/h11033036.png" />-designs are quite useful in recursive constructions. There exist <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110330/h11033037.png" /> for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110330/h11033038.png" /> even, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110330/h11033039.png" />, with two exceptions: there is no <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110330/h11033040.png" /> and there is no <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110330/h11033041.png" /> [[#References|[a1]]]. The existence of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110330/h11033042.png" /> for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110330/h11033043.png" /> odd remains open, see [[#References|[a5]]]. The only known case where an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110330/h11033044.png" /> exists but an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110330/h11033045.png" /> does not is for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110330/h11033046.png" />. | + | An $ H ^ {*} ( s,2n ) $ |
| | + | is an $ H ( s,2n ) $ |
| | + | in which there is a subset $ W $ |
| | + | of $ V $, |
| | + | $ | W | = 2n - s $, |
| | + | such that no pair of elements from $ W $ |
| | + | appears in the design. $ * $- |
| | + | designs are quite useful in recursive constructions. There exist $ H ^ {*} ( s,2n ) $ |
| | + | for $ s $ |
| | + | even, $ n \leq s \leq 2n - 2 $, |
| | + | with two exceptions: there is no $ H ^ {*} ( 2,4 ) $ |
| | + | and there is no $ H ^ {*} ( 6,12 ) $[[#References|[a1]]]. The existence of $ H ^ {*} ( s,2n ) $ |
| | + | for $ s $ |
| | + | odd remains open, see [[#References|[a5]]]. The only known case where an $ H ( s,2n ) $ |
| | + | exists but an $ H ^ {*} ( s,2n ) $ |
| | + | does not is for $ s = n = 6 $. |
| | | | |
| − | The pairs of elements in the cells of an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110330/h11033047.png" /> can be thought of as the edges of an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110330/h11033048.png" />-regular [[Graph|graph]] on the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110330/h11033049.png" />-set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110330/h11033050.png" />, the underlying graph of the Howell design. The existence of an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110330/h11033051.png" /> is equivalent to the existence of a pair of orthogonal one-factorizations of the underlying graph of the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110330/h11033052.png" /> (cf. [[One-factorization|One-factorization]]). The underlying graph of an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110330/h11033053.png" /> is the complete graph <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110330/h11033054.png" />, and the underlying graph of an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110330/h11033055.png" /> is the cocktail party graph <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110330/h11033056.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110330/h11033057.png" /> is a [[One-factor|one-factor]]. An <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110330/h11033058.png" /> with underlying graph <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110330/h11033059.png" /> is equivalent to a pair of mutually [[Orthogonal Latin squares|orthogonal Latin squares]] of order <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110330/h11033060.png" />. The general problem of determining which graphs are the underlying graphs of a Howell design remains open (1996), see [[#References|[a3]]]. | + | The pairs of elements in the cells of an $ H ( s,2n ) $ |
| | + | can be thought of as the edges of an $ s $- |
| | + | [[regular graph]] on the $ 2n $- |
| | + | set $ V $, |
| | + | the underlying graph of the Howell design. The existence of an $ H ( s,2n ) $ |
| | + | is equivalent to the existence of a pair of orthogonal one-factorizations of the underlying graph of the $ H ( s,2n ) $( |
| | + | cf. [[One-factorization|One-factorization]]). The underlying graph of an $ H ( 2n - 1,2n ) $ |
| | + | is the complete graph $ K _ {2n } $, |
| | + | and the underlying graph of an $ H ( 2n - 2,2n ) $ |
| | + | is the [[cocktail party graph]] $ K _ {2n } - f $, |
| | + | where $ f $ |
| | + | is a [[One-factor|one-factor]]. An $ H ( n,2n ) $ |
| | + | with underlying graph $ K _ {n,n } $ |
| | + | is equivalent to a pair of mutually [[Orthogonal Latin squares|orthogonal Latin squares]] of order $ n $. |
| | + | The general problem of determining which graphs are the underlying graphs of a Howell design remains open (1996), see [[#References|[a3]]]. |
| | | | |
| − | Several special types of Howell designs have been studied, including <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110330/h11033061.png" />-designs, skew designs, complementary designs, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110330/h11033062.png" />-complementary designs, cyclic Howell designs (used for Howell movements in duplicate bridge), and Howell designs with Howell sub-designs (see [[#References|[a3]]] [[#References|[a4]]]). | + | Several special types of Howell designs have been studied, including $ ** $- |
| | + | designs, skew designs, complementary designs, $ * $- |
| | + | complementary designs, cyclic Howell designs (used for Howell movements in duplicate bridge), and Howell designs with Howell sub-designs (see [[#References|[a3]]] [[#References|[a4]]]). |
| | | | |
| − | A <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110330/h11033064.png" />-dimensional Howell design, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110330/h11033065.png" />, is a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110330/h11033066.png" />-dimensional array in which every cell either is empty or contains an unordered pair of elements from a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110330/h11033067.png" />-set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110330/h11033068.png" /> and such that each two-dimensional projection is an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110330/h11033069.png" />. An <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110330/h11033070.png" /> is called a Howell cube. An <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110330/h11033071.png" /> is equivalent to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110330/h11033072.png" /> mutually orthogonal one-factorizations of the underlying graph. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110330/h11033073.png" /> denote the maximum value of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110330/h11033074.png" /> such that an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110330/h11033075.png" /> exists. Very little is known about upper bounds for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110330/h11033076.png" />. It is easy to see that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110330/h11033077.png" />, and it has been conjectured that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110330/h11033078.png" />. See [[#References|[a3]]], [[#References|[a2]]] for results on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110330/h11033079.png" /> and existence results on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110330/h11033080.png" />. | + | A $ d $- |
| | + | dimensional Howell design, $ H _ {d} ( s,2n ) $, |
| | + | is a $ d $- |
| | + | dimensional array in which every cell either is empty or contains an unordered pair of elements from a $ 2n $- |
| | + | set $ V $ |
| | + | and such that each two-dimensional projection is an $ H ( s,2n ) $. |
| | + | An $ H _ {3} ( s,2n ) $ |
| | + | is called a Howell cube. An $ H _ {d} ( s,2n ) $ |
| | + | is equivalent to $ d $ |
| | + | mutually orthogonal one-factorizations of the underlying graph. Let $ \nu ( s,2n ) $ |
| | + | denote the maximum value of $ d $ |
| | + | such that an $ H _ {d} ( s,2n ) $ |
| | + | exists. Very little is known about upper bounds for $ \nu ( s,2n ) $. |
| | + | It is easy to see that $ \nu ( s,2n ) \leq s - 1 $, |
| | + | and it has been conjectured that $ \nu ( s,2n ) \leq n - 1 $. |
| | + | See [[#References|[a3]]], [[#References|[a2]]] for results on $ \nu ( s,2n ) $ |
| | + | and existence results on $ H _ {d} ( s,2n ) $. |
| | | | |
| | The survey article [[#References|[a3]]] includes results and references on Howell designs. | | The survey article [[#References|[a3]]] includes results and references on Howell designs. |
A Howell design of side $ s $
and order $ 2n $,
or more briefly an $ H ( s,2n ) $,
is an $ ( s \times s ) $-
array in which each cell is either empty or contains an unordered pair of distinct elements from some $ 2n $-
set $ V $
such that:
1) every element of $ V $
occurs in precisely one cell of each row and each column;
2) every unordered pair of elements from $ V $
is in at most one cell of the array. It follows immediately from the definition of an $ H ( s,2n ) $
that $ n \leq s \leq 2n - 1 $.
An example of a Howell design is the following $ H ( 4,6 ) $:
<tbody> </tbody> | $ \alpha $
0 | | 1 3 | $ \infty $
2 | | | | | | 2 3 | $ \alpha $
1 | $ \infty $
0 | | | | | | | $ \infty $
3 | $ \alpha $
2 | 0 1 | | | | | | $ \infty $
1 | 0 2 | | $ \alpha $
3 |
|
An $ H ( 2n - 1,2n ) $
is also called a Room square of side $ 2n - 1 $.
At the other extreme, the existence of a pair of mutually orthogonal Latin squares implies the existence of an $ H ( n,2n ) $.
The existence of Howell designs has been completely determined [a1], [a5]: Let $ s $
and $ n $
be positive integers such that $ 0 \leq n \leq s \leq 2n - 1 $.
There exists an $ H ( s,2n ) $
if and only if $ ( s,2n ) \neq ( 2,4 ) , ( 3,4 ) , ( 5,6 ) $
or $ ( 5,8 ) $.
The proof uses a variety of direct and recursive constructions.
An $ H ^ {*} ( s,2n ) $
is an $ H ( s,2n ) $
in which there is a subset $ W $
of $ V $,
$ | W | = 2n - s $,
such that no pair of elements from $ W $
appears in the design. $ * $-
designs are quite useful in recursive constructions. There exist $ H ^ {*} ( s,2n ) $
for $ s $
even, $ n \leq s \leq 2n - 2 $,
with two exceptions: there is no $ H ^ {*} ( 2,4 ) $
and there is no $ H ^ {*} ( 6,12 ) $[a1]. The existence of $ H ^ {*} ( s,2n ) $
for $ s $
odd remains open, see [a5]. The only known case where an $ H ( s,2n ) $
exists but an $ H ^ {*} ( s,2n ) $
does not is for $ s = n = 6 $.
The pairs of elements in the cells of an $ H ( s,2n ) $
can be thought of as the edges of an $ s $-
regular graph on the $ 2n $-
set $ V $,
the underlying graph of the Howell design. The existence of an $ H ( s,2n ) $
is equivalent to the existence of a pair of orthogonal one-factorizations of the underlying graph of the $ H ( s,2n ) $(
cf. One-factorization). The underlying graph of an $ H ( 2n - 1,2n ) $
is the complete graph $ K _ {2n } $,
and the underlying graph of an $ H ( 2n - 2,2n ) $
is the cocktail party graph $ K _ {2n } - f $,
where $ f $
is a one-factor. An $ H ( n,2n ) $
with underlying graph $ K _ {n,n } $
is equivalent to a pair of mutually orthogonal Latin squares of order $ n $.
The general problem of determining which graphs are the underlying graphs of a Howell design remains open (1996), see [a3].
Several special types of Howell designs have been studied, including $ ** $-
designs, skew designs, complementary designs, $ * $-
complementary designs, cyclic Howell designs (used for Howell movements in duplicate bridge), and Howell designs with Howell sub-designs (see [a3] [a4]).
A $ d $-
dimensional Howell design, $ H _ {d} ( s,2n ) $,
is a $ d $-
dimensional array in which every cell either is empty or contains an unordered pair of elements from a $ 2n $-
set $ V $
and such that each two-dimensional projection is an $ H ( s,2n ) $.
An $ H _ {3} ( s,2n ) $
is called a Howell cube. An $ H _ {d} ( s,2n ) $
is equivalent to $ d $
mutually orthogonal one-factorizations of the underlying graph. Let $ \nu ( s,2n ) $
denote the maximum value of $ d $
such that an $ H _ {d} ( s,2n ) $
exists. Very little is known about upper bounds for $ \nu ( s,2n ) $.
It is easy to see that $ \nu ( s,2n ) \leq s - 1 $,
and it has been conjectured that $ \nu ( s,2n ) \leq n - 1 $.
See [a3], [a2] for results on $ \nu ( s,2n ) $
and existence results on $ H _ {d} ( s,2n ) $.
The survey article [a3] includes results and references on Howell designs.
References
| [a1] | B.A. Anderson, P.J. Schellenberg, D.R. Stinson, "The existence of Howell designs of even side" J. Combin. Th. A , 36 (1984) pp. 23–55 |
| [a2] | J.H. Dinitz, "Howell designs" C.J. Colbourn (ed.) J.H. Dinitz (ed.) , CRC Handbook of Combinatorial Designs , CRC (1996) pp. 381–385 |
| [a3] | J.H. Dinitz, D.R. Stinson, "Room squares and related designs" J.H. Dinitz (ed.) D.R. Stinson (ed.) , Contemporary Design Theory: A Collection of Surveys , Wiley (1992) pp. 137–204 |
| [a4] | E.R. Lamken, S.A. Vanstone, "The existence of skew Howell designs of side 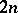 and order and order 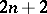 " J. Combin. Th. A , 54 (1990) pp. 20–40 " J. Combin. Th. A , 54 (1990) pp. 20–40 |
| [a5] | D.R. Stinson, "The existence of Howell designs of odd side" J. Combin. Th. A , 32 (1982) pp. 53–65 |
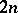 and order
and order 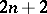 " J. Combin. Th. A , 54 (1990) pp. 20–40
" J. Combin. Th. A , 54 (1990) pp. 20–40