One-factor
of a graph
Suppose $G$ is a (simple) graph. A matching in $G$ is a set of pairwise-disjoint edges in $G$. A one-factor or spanning matching is a set of edges such that every vertex of $G$ occurs in exactly one edge.
Not every graph $G$ has a one-factor. One obvious necessary condition is that $G$ has no connected component with an odd number of vertices. However this is not a sufficient condition. The smallest graph connected with an even number of vertices but no one-factor is:
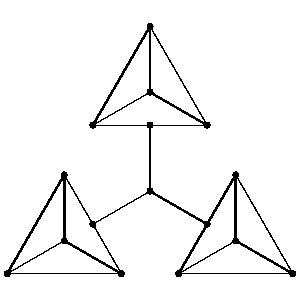
Figure: o110060a
One-factors were first studied by W.T. Tutte, who proved the following characterization. If $W$ is any subset of the vertex set $V(G)$ of $G$, let $G-W$ denote the graph constructed from $G$ by deleting $W$ and all edges touching members of $W$. The components of $G-W$ are odd or even according as they have an odd or even number of vertices. Write $\phi(W)$ for the number of odd components of $G-W$.
Tutte's theorem [a6]: $G$ contains a one-factor if and only if $\phi(W)\leq|W|$ whenever $W\leq V(G)$.
A consequence is that for $n$ even, any regular graph of degree $n-1$ on $2n$ vertices has a one-factor.
A bridge in a graph $G$ is an edge whose deletion disconnects $G$.
Petersen's theorem [a4]: A bridgeless cubic graph contains a one-factor.
This has been generalized by T. Schönberger [a5], who proved that every edge of a bridgeless cubic graph lies in a one-factor. C. Berge [a1] and A.B. Cruse [a3] proved another generalization. If $W$ is any set of vertices of $G$, let $z_G(W)$ be the number of edges of $G$ with exactly one end-point in $W$.
The Berge–Cruse theorem: If $G$ is a regular graph of degree $d$ with an even number of vertices, and if $z_G(W)\leq d-1$ for all odd-order subsets $W$ of $V(G)$, then each edge of $G$ belongs to some one-factor.
Consequences are [a3]:
1) if $G$ is a regular graph of degree $d$ with $2m$ vertices and $d\geq m$ ($m$ odd) or $d\geq m-1$ ($m$ even), then every edge of $G$ belongs to some one-factor;
2) if $G$ is a regular graph of valency $d$ with $m$ vertices and $d\geq m\geq2$, then $G$ contains at least
$$d-m+2\left\lfloor\frac{5(m+5)}{112}\right\rfloor$$
disjoint one-factors.
A number of results have been proved concerning whether a graph of a certain description (usually a quite sparse graph) contains a one-factor.
Important references include [a2], and [a7].
References
| [a1] | C. Berge, "Graphs and hypergraphs" , North-Holland (1973) (Translated from French) |
| [a2] | J. Bosák, "Decomposition of graphs" , Kluwer Acad. Publ. (1990) |
| [a3] | A.B. Cruse, "A note on one-factors in certain regular multigraphs" Discrete Math. , 18 (1977) pp. 213–216 |
| [a4] | J. Petersen, "Die Theorie der regulären Graphes" Acta Math. , 15 (1981) pp. 193–220 |
| [a5] | T. Schönberger, "Ein Beweis des Peterschen Graphensatzes" Acta Sci. Math. Szeged , 7 (1934) pp. 51–57 |
| [a6] | W.T. Tutte, "The factorizations of linear graphs" J. London Math. Soc. , 22 (1947) pp. 459–474 |
| [a7] | W.D. Wallis, "One-factorizations" , Kluwer Acad. Publ. (1997) |
One-factor. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=One-factor&oldid=51403