One-factorization
of a graph
If $ G $ is a graph, then a factorization of $ G $ is a set of spanning subgraphs of $ G $ that are pairwise edge-disjoint (i.e., no two have a common edge) and whose union is all of $ G $. A one-factorization of $ G $ is a decomposition of the edge-set of $ G $ into edge-disjoint one-factors (cf. One-factor).
In order to have a one-factorization, a graph must have an even number of vertices and must be regular: if $ G $ decomposes into $ d $ disjoint one-factors, then every vertex of $ G $ must lie on precisely $ d $ edges. These conditions are not sufficient, since there is the following theorem: A regular graph with a bridge (cf. One-factor) cannot have a one-factorization (except for the trivial case where the graph is itself a one-factor).
If the degree increases with the number of vertices, the situation is different. It has been conjectured that a regular graph with $ 2n $ vertices and degree greater than $ n $ will always have a one-factorization; this has only been proved in a very few cases, such as degree $ 2n - 4 $, degree $ 2n - 5 $, and degree at least $ { {12n } / 7 } $, [a7], [a20]. On the other hand, there are regular graphs with degree near to half the number of vertices and without one-factorizations.
One can prove the existence of one-factorizations in many classes of graphs. Of basic importance are the complete graphs. The complete graph $ K _ {2n } $ has a one-factorization for all $ n $. The $ n $- vertex cycle $ C _ {n} $ has a one-factorization if and only if $ n $ is even. The regular complete bipartite graph $ K _ {n,n } $( cf. Graph, bipartite) always has a one-factorization. One-factorizations of complete bipartite graphs are equivalent to Latin squares (cf. Latin square).
Some other factorizations of complete graphs are important. A near-one-factor in $ K _ {2n - 1 } $ is a set of $ n - 1 $ edges which cover all but one vertex. A set of near-one-factors which covers every edge precisely once is called a near-one-factorization. $ K _ {2n - 1 } $ has a near-one-factorization for every $ n $. It is in fact obvious that any near-one-factorization of $ K _ {2n - 1 } $ can be converted to a one-factorization of $ K _ {2n } $ by adding a vertex $ \infty $ and joining $ \infty $ to the isolated vertex in each factor. It follows that each vertex appears precisely once as an isolate in a near-one-factorization. (This also follows immediately by adding degrees.)
Theoretical considerations aside, it is often important to be able to construct a one-factorization (or a set of one-factorizations) of $ K _ {2n } $, for a particular value $ 2n $. A hill-climbing algorithm was described by J.H. Dinitz and D.R. Stinson [a10]. In order to use the hill-climbing approach, it is necessary to formulate the search for a one-factorization as an optimization problem. One first defines a matching to be a set $ {\mathcal F} $ of pairs of the form $ \{ f _ {i} , ( x,y ) \} $, where each edge $ ( x,y ) $ of $ K _ {2n } $ occurs as the latter entry in at most one of the pairs, and where $ {\mathcal F} $ contains no two pairs $ \{ f _ {i} , ( x,y ) \} $ and $ \{ f _ {i} , ( x,z ) \} $ with $ y \neq z $. The cost $ c ( {\mathcal F} ) $ of a matching $ {\mathcal F} $ is $ n ( 2n - 1 ) - | {\mathcal F} | $. Then $ {\mathcal F} $ is a one-factorization if and only if $ c ( {\mathcal F} ) = 0 $. There is no guarantee that repeated applications of these heuristics will produce a one-factorization; however, Dinitz and Stinson [a10] report no failures in over a million trials.
A starter in an Abelian group $ G $ of order $ 2n - 1 $ is an ordered partition of the non-zero members of $ G $ into $ 2 $- sets $ \{ x _ {1} ,y _ {1} \} \dots \{ x _ {n - 1 } ,y _ {n - 1 } \} $ with the property that the $ 2n - 2 $ differences $ \pm ( x _ {1} - y _ {1} ) \dots \pm ( x _ {n - 1 } - y _ {n - 1 } ) $ are all different and therefore contain every non-zero element of $ G $ precisely once. From a starter $ F $ one constructs a set of $ 2n - 1 $ factors by systematically adding elements of $ G $ to $ F $. This process is called developing $ F $ in $ G $. Many useful small examples of one-factorizations are constructed using starters. The starter consisting of all the pairs $ \{ x, - x \} $, where $ x $ ranges through the non-zero elements of some group, is called a patterned starter.
There is only one one-factor in $ K _ {2} $, and it (trivially) constitutes the unique one-factorization. Similarly, $ K _ {4} $ has just three one-factors, and together they form a factorization. There are six different one-factorizations of $ K _ {6} $, $ 6240 $ of $ K _ {8} $, $ 1.255.566.720 $ of $ K _ {10 } $[a11], and $ 252.282.619.805.368.320 $ of $ K _ {12 } $[a9]; no larger numbers are known.
Two one-factorizations $ {\mathcal F} $ and $ {\mathcal H} $ of $ G $, say
$$ {\mathcal F} = \{ F _ {1} \dots F _ {k} \} \textrm{ and } {\mathcal H} = \{ H _ {1} \dots H _ {k} \} , $$
are called isomorphic if there exists a mapping $ \phi $ from the vertex-set of $ G $ onto itself such that
$$ \{ F _ {1} \phi \dots F _ {k} \phi \} = \{ H _ {1} \dots H _ {k} \} , $$
where $ F _ {i} \phi $ is the set of all edges $ \{ x \phi,y \phi \} $, where $ \{ x,y \} $ is an edge in $ {\mathcal F} $. There is a unique one-factorization of $ K _ {2n } $, up to isomorphism, for $ 2n = 2,4,6 $. There are exactly six for $ K _ {8} $[a8], $ 396 $ of $ K _ {10 } $; they are listed in [a11] (see also [a12]) and $ 526.915.620 $ isomorphism classes of one-factorizations of $ K _ {12 } $[a9]. To discuss isomorphism of factorizations, various invariants have been used. The number of isomorphism classes of one-factorizations of $ K _ {2n } $ tends to infinity as $ n $ does [a4], [a16].
An object whose only automorphism is the identity is called rigid or asymmetric. There are no rigid one-factorizations on $ 2 $, $ 4 $, $ 6 $, or $ 8 $ points. However, there is a rigid one-factorization of $ K _ {2n } $ whenever $ 2n \geq 10 $. In fact, the number of isomorphism classes of rigid one-factorizations of $ K _ {2n } $ goes to infinity with $ n $.
A one-factorization is called perfect if the union of any two factors is a Hamilton cycle (cf. Hamiltonian tour). Perfect one-factorizations exist for many orders, and no order $ n $( greater than 1) is known for which no perfect one-factorization of $ K _ {2n } $ exists, but the existence question is not yet (1996) settled.
The following theorem holds [a2], [a3]: If $ p $ is an odd prime, then $ K _ {p + 1 } $ and $ K _ {2p } $ have perfect factorizations.
Apart from these two constructions, all other known perfect one-factorizations have been found by ad-hoc methods, using starters.
Various techniques have been studied which produce a new graph from two given graphs. There is some interest in the following problems: Given a form of graph product, what conditions on graphs $ G $ and $ H $ imply that the product of $ G $ and $ H $ has a one-factorization? This has been studied for Cartesian products, wreath products and tensor products. References include [a1], [a13], [a14], [a15], [a19], [a23], [a27].
One-factorizations are frequently used to schedule sporting tournaments. One considers a graph whose vertices are competing teams; an edge indicates that the two teams must play against each other. The set of games held simultaneously is called a round. Suppose each team must compete in every round. Clearly, the games that form a round form a one-factor in the underlying graph. If a round robin tournament for $ 2n $ teams is to be played in the minimum number of sessions, one requires a one-factorization of $ K _ {2n } $. If there are $ 2n - 1 $ teams, the relevant structure is a near-one-factorization of $ K _ {2n - 1 } $. In each case the factorization is called the schedule of the tournament.
Papers on this application include [a5], [a21], [a22], [a24], [a28], [a29], [a30].
Some general surveys on one-factorizations are [a18], [a25] and [a26]. Books on related topics include [a6] and [a17].
References
| [a1] | B. Alspach, J.C. George, "One-factorization of tensor products of graphs" , Topics in Combinatorics and Graph Theory , Physica-Verlag (1990) pp. 41–46 |
| [a2] | B.A. Anderson, "Finite topologies and Hamiltonian paths" J. Combin. Th. , 14B (1973) pp. 87–93 |
| [a3] | B.A. Anderson, "Symmetry groups of some perfect one-factorization of complete graphs" Discrete Math. , 18 (1977) pp. 227–234 |
| [a4] | B.A. Anderson, M.M. Barge, D. Morse, "A recursive construction of asymmetric 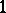 -factorizations" Aequationes Math. , 15 (1977) pp. 201–211 -factorizations" Aequationes Math. , 15 (1977) pp. 201–211 |
| [a5] | A.F. Beecham, A.C. Hurley, "A scheduling problem with a simple graphical solution" J. Austral. Math. Soc. , 21B (1980) pp. 486–495 |
| [a6] | J. Bosák, "Decomposition of graphs" , Kluwer Acad. Publ. (1990) |
| [a7] | A.G. Chetwynd, A.J.W. Hilton, "Regular graphs of high degree are 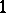 -factorizable" Proc. London Math. Soc. (3) , 50 (1985) pp. 193–206 -factorizable" Proc. London Math. Soc. (3) , 50 (1985) pp. 193–206 |
| [a8] | L.E. Dickson, F.H. Safford, "Solution to problem 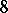 (group theory)" Amer. Math. Monthly , 13 (1906) pp. 150–151 (group theory)" Amer. Math. Monthly , 13 (1906) pp. 150–151 |
| [a9] | J.H. Dinitz, D.K. Garnick, B.D. McKay, "There are 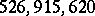 non-isomorphic one-factorizations of non-isomorphic one-factorizations of  " J. Combin. Designs , 2 (1994) pp. 273–285 " J. Combin. Designs , 2 (1994) pp. 273–285 |
| [a10] | J.H. Dinitz, D.R. Stinson, "A hill-climbing algorithm for the construction of one-factorizations and room squares" SIAM J. Algebraic Discrete Methods , 8 (1987) pp. 430–438 |
| [a11] | E.N. Gelling, "On one-factorizations of a complete graph and the relationship to round-robin schedules" Ph.D. Thesis, Univ. Victoria, Canada (1973) |
| [a12] | E.N. Gelling, R.E. Odeh, "On 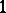 -factorizations of the complete graph and the relationship to round-robin schedules" Congressus Numerantium , 9 (1974) pp. 213–221 -factorizations of the complete graph and the relationship to round-robin schedules" Congressus Numerantium , 9 (1974) pp. 213–221 |
| [a13] | P.E. Himelwright, J.E. Williamson, "On 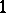 -factorability and edge-colorability of cartesian products of graphs" Elemente der Math. , 29 (1974) pp. 66–67 -factorability and edge-colorability of cartesian products of graphs" Elemente der Math. , 29 (1974) pp. 66–67 |
| [a14] | P. Himelwright, W.D. Wallis, J.E. Williamson, "On one-factorizations of compositions of graphs" J. Graph Th. , 6 (1982) pp. 75–80 (Erratum: J. Graph Theory 8 (1984), 185–186) |
| [a15] | A. Kotzíg, "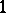 -factorizations of cartesian products of regular graphs" J. Graph Th. , 3 (1979) pp. 23–34 -factorizations of cartesian products of regular graphs" J. Graph Th. , 3 (1979) pp. 23–34 |
| [a16] | C.C. Lindner, E. Mendelsohn, A. Rosa, "On the number of  -factorizations of the complete graph" J. Combin. Th. , 20A (1976) pp. 265–282 -factorizations of the complete graph" J. Combin. Th. , 20A (1976) pp. 265–282 |
| [a17] | L. Lovász, M.D. Plummer, "Matching theory" , North-Holland (1986) |
| [a18] | E. Mendelsohn, A. Rosa, "One-factorizations of the complete graph -- a survey" J. Graph Th. , 9 (1985) pp. 43–65 |
| [a19] | E.T. Parker, "Edge-coloring numbers of some regular graphs" Proc. Amer. Math. Soc. , 37 (1973) pp. 423–424 |
| [a20] | A. Rosa, W.D. Wallis, "Premature sets of 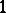 -factors, or, how not to schedule round-robin tournaments" Discrete Appl. Math. , 4 (1982) pp. 291–297 -factors, or, how not to schedule round-robin tournaments" Discrete Appl. Math. , 4 (1982) pp. 291–297 |
| [a21] | K.G. Russell, "Balancing carry-over effects in round robin tournaments" Biometrika , 67 (198) pp. 127–131 |
| [a22] | T.H. Straley, "Scheduling designs for a league tournament" Ars Combin. , 15 (1983) pp. 193–200 |
| [a23] | W.D. Wallis, "One-factorizations of wreath products" , Combinatorial Mathematics VIII , Lecture Notes in Mathematics , 884 , Springer (1981) pp. 337–345 |
| [a24] | W.D. Wallis, "A tournament problem" J. Austral. Math. Soc. , 24B (1983) pp. 289–291 |
| [a25] | W.D. Wallis, "One-factorizations of complete graphs" , Contemporary Design Theory , Wiley (1992) pp. 593–631 |
| [a26] | W.D. Wallis, "One-factorizations" , Kluwer Acad. Publ. (1997) |
| [a27] | W.D. Wallis, Z. Wang, "On one-factorizations of cartesian products" Congressus Numerantium , 49 (1985) pp. 237– 245 |
| [a28] | D. de Werra, "Scheduling in sports" , Studies on Graphs and Discrete Programming , North-Holland (1981) pp. 381–395 |
| [a29] | D. de Werra, "On the multiplication of divisions: the use of graphs for sports scheduling" Networks , 15 (1985) pp. 125–136 |
| [a30] | D. de Werra, L. Jacot-Descombes, P. Masson, "A constrained sports scheduling problem" Discrete Appl. Math. , 26 (1990) pp. 41–49 |
One-factorization. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=One-factorization&oldid=51408