Difference between revisions of "White noise analysis"
m (link) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| − | Since its inception in the nineteen seventies [[#References|[a1]]]–, white noise analysis has developed into a viable framework for stochastic and infinite-dimensional analysis [[#References|[a4]]]–[[#References|[a6]]], with a growing number of applications in various disciplines, most notably perhaps in quantum physics. Informally speaking, the role here of (Gaussian, continuous parameter) [[White noise|white noise]] — a generalized random process (cf. [[Stochastic process, generalized|Stochastic process, generalized]]) with independent values at each point [[#References|[a7]]] — is that of an infinite system of coordinates on which to base an infinite-dimensional calculus. More precisely, the starting point is the | + | <!-- |
| + | w0977601.png | ||
| + | $#A+1 = 165 n = 2 | ||
| + | $#C+1 = 165 : ~/encyclopedia/old_files/data/W097/W.0907760 White noise analysis | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| + | |||
| + | {{TEX|auto}} | ||
| + | {{TEX|done}} | ||
| + | |||
| + | Since its inception in the nineteen seventies [[#References|[a1]]]–, white noise analysis has developed into a viable framework for stochastic and infinite-dimensional analysis [[#References|[a4]]]–[[#References|[a6]]], with a growing number of applications in various disciplines, most notably perhaps in quantum physics. Informally speaking, the role here of (Gaussian, continuous parameter) [[White noise|white noise]] — a generalized random process (cf. [[Stochastic process, generalized|Stochastic process, generalized]]) with independent values at each point [[#References|[a7]]] — is that of an infinite system of coordinates on which to base an infinite-dimensional calculus. More precisely, the starting point is the $ L _ {2} $- | ||
| + | space of the white noise measure, which is then imbedded into [[Gel'fand triple]]s of test, respectively generalized, function spaces with suitable properties. In particular, the test functions will be chosen sufficiently smooth to admit an infinite-dimensional differential calculus, which is then transported to the generalized functions by duality. With these established, various concepts have natural generalizations to the infinite-dimensional setting. Examples are: the gradient, Laplacian(s) [[#References|[a4]]], Chapt. 6, the rotation group [[#References|[a8]]], Fourier analysis, and Dirichlet forms. Below some of this is outlined; a comprehensive presentation can be found in [[#References|[a4]]]. | ||
==(Gaussian) white noise.== | ==(Gaussian) white noise.== | ||
| − | This is a generalized random process | + | This is a generalized random process $ \omega $[[#References|[a1]]], [[#References|[a7]]]; for any Schwartz test function $ f \in {\mathcal S} ( \mathbf R ) $ |
| + | the "smeared out" process $ \langle \omega , f \rangle $ | ||
| + | is a Gaussian [[Random variable|random variable]] $ X _ {f} $ | ||
| + | with mean zero and covariance | ||
| − | + | $$ | |
| + | {\mathsf E} ( X _ {f} X _ {g} ) = \int\limits f( t) g( t) dt = ( f, g) . | ||
| + | $$ | ||
| − | In terms of the white noise measure | + | In terms of the white noise measure $ \mu $ |
| + | and its characteristic function $ C $, | ||
| + | one has | ||
| − | + | $$ | |
| + | C( f ) = {\mathsf E} ( e ^ {i \langle \omega , f \rangle } ) = \ | ||
| + | \int\limits d \mu [ \omega ] e ^ {i \langle \omega , f\rangle } = \ | ||
| + | e ^ {- ( 1/2) \int\limits f ^ { 2 } ( t ) dt } , | ||
| + | $$ | ||
| − | + | $$ | |
| + | f \in {\mathcal S} ( \mathbf R ) . | ||
| + | $$ | ||
| − | By extending test functions to | + | By extending test functions to $ L _ {2} ( \mathbf R ) $ |
| + | one obtains a version of Wiener's [[Brownian motion|Brownian motion]] process $ B ( \cdot ) $ | ||
| + | by observing that | ||
| − | + | $$ | |
| + | B( t) \equiv X( 1 I _ {[ 0, t] } ) = \int\limits _ { 0 } ^ { t } | ||
| + | \omega ( \tau ) d \tau | ||
| + | $$ | ||
expresses the Wiener process in terms of white noise [[#References|[a1]]], [[#References|[a2]]]. In this sense Brownian functionals can be considered as functionals of white noise. A large collection of the latter is provided by those of finite variance, i.e. by the Hilbert space | expresses the Wiener process in terms of white noise [[#References|[a1]]], [[#References|[a2]]]. In this sense Brownian functionals can be considered as functionals of white noise. A large collection of the latter is provided by those of finite variance, i.e. by the Hilbert space | ||
| − | + | $$ | |
| + | ( L _ {2} ) \equiv L _ {2} ( {\mathcal S} ^ {*} ( \mathbf R ) , d \mu ) . | ||
| + | $$ | ||
| − | The polynomials in | + | The polynomials in $ X _ {f} $, |
| + | $ f \in {\mathcal S} ( \mathbf R ) $, | ||
| + | form a dense subspace in $ ( L _ {2} ) $, | ||
| + | hence the monomials $ X _ {f} $ | ||
| + | are a total set; to orthogonalize them one introduces the "normal ordered" , or "Wick ordered" or "Hermite" , products | ||
| − | + | $$ | |
| + | : X _ {f _ {1} } \dots X _ {f _ {n} } : = \ | ||
| + | ( 1 - P _ {n-} 1 ) X _ {f _ {1} } \dots X _ {f _ {n} } , | ||
| + | $$ | ||
| − | where | + | where $ P _ {n} $ |
| + | projects onto the subspace of polynomials of order at most $ n $. | ||
| + | They are related to multiple Wiener integrals (cf. [[Wiener integral|Wiener integral]]) [[#References|[a9]]] through | ||
| − | + | $$ | |
| + | : X _ {f} ^ {n} : = \int\limits f( t _ {1} ) \dots f ( t _ {n} ) \ | ||
| + | d B ( t _ {1} ) \dots dB( t _ {n} ) . | ||
| + | $$ | ||
| − | By linearity and continuity these expressions extend from product kernel functions | + | By linearity and continuity these expressions extend from product kernel functions $ F ^ { ( n) } = \prod f _ {i} $ |
| + | to symmetric $ L _ {2} $- | ||
| + | kernel functions $ F ^ { ( n) } ( t _ {1} \dots t _ {n} ) \in \mathop{\rm Sy} L _ {2} ( \mathbf R ^ {n} ) $; | ||
| + | as a result one obtains an isomorphism between the white noise Hilbert space $ ( L _ {2} ) $ | ||
| + | and a Boson Fock space | ||
| − | + | $$ | |
| + | ( L _ {2} ) \simeq \oplus _ { n } \mathop{\rm Sy} L _ {2} ( \mathbf R ^ {n} ,\ | ||
| + | n ! dt ) . | ||
| + | $$ | ||
| − | Another characterization of | + | Another characterization of $ ( L _ {2} ) $ |
| + | is through the "S-" or "T-transform" | ||
| − | + | $$ | |
| + | T: \Phi \rightarrow E ( \Phi e ^ {iX _ {f} } ) = ( T \Phi ) ( f ) , | ||
| + | $$ | ||
| − | + | $$ | |
| + | S: \Phi \rightarrow E( \Phi [ \cdot + f ]) = ( S \Phi )( f ). | ||
| + | $$ | ||
| − | They are related through | + | They are related through $ ( S \Phi )( f ) = C( f ) \cdot ( T \Phi )(- i f ) = E( \Phi : e ^ {X _ {f} } : ) $. |
==Generalized functions.== | ==Generalized functions.== | ||
| − | The main interest of the above constructions is to go beyond them, to consider functionals such as e.g. the "action integral" for Brownian motion | + | The main interest of the above constructions is to go beyond them, to consider functionals such as e.g. the "action integral" for Brownian motion $ \int : \omega ^ {2} ( t) : dt $; |
| + | or "Donsker d-functionDonsker's d-function" $ \delta ( B( t) - a) $. | ||
| − | Checking whether their kernel functions are in the Fock space, one finds that in the first example the kernel functions | + | Checking whether their kernel functions are in the Fock space, one finds that in the first example the kernel functions $ F ^ { ( n) } $ |
| + | are given by $ F ^ { ( n) } ( t _ {1} \dots t _ {n} ) = \delta _ {n ,2 } \delta ( t _ {1} - t _ {2} ) $, | ||
| + | which is clearly not square integrable. In the second example the $ F ^ { ( n) } $ | ||
| + | are square integrable, but their norms fail to be square summable. Thus, a good extension of $ ( L _ {2} ) $ | ||
| + | should be one that relaxes both the $ L _ {2} $- | ||
| + | property of the kernel functions and the square summability of their norms. | ||
A standard procedure to enlarge Hilbert spaces is through the construction of Gel'fand triples, such as e.g. | A standard procedure to enlarge Hilbert spaces is through the construction of Gel'fand triples, such as e.g. | ||
| − | + | $$ | |
| + | {\mathcal S} ( \mathbf R ) \subset L _ {2} ( \mathbf R ) \subset {\mathcal S} ^ {*} | ||
| + | ( \mathbf R ) , | ||
| + | $$ | ||
| − | with | + | with $ {\mathcal S} $ |
| + | defined as a countable (intersection of) Hilbert space(s): | ||
| − | + | $$ | |
| + | {\mathcal S} = \cap _ { p= } 1 ^ \infty {\mathcal S} _ {p} ,\ \ | ||
| + | {\mathcal S} _ {p} = D( A ^ {p} ) , | ||
| + | $$ | ||
| − | where | + | where $ A $ |
| + | is the self-adjoint operator $ A = - d ^ {2} / dt ^ {2} + t ^ {2} + 1 $ | ||
| + | in $ L _ {2} ( \mathbf R , dt ) $. | ||
| + | Here one invokes the second quantization $ \Gamma $[[#References|[a10]]] of operators such as $ A $. | ||
| + | It is given as a linear operator in $ ( L _ {2} ) $ | ||
| + | by its action on normal ordered monomials: | ||
| − | + | $$ | |
| + | \Gamma ( A) : X _ {f _ {1} } \dots X _ {f _ {1} } : = \ | ||
| + | : X _ {A f _ {1} } \dots X _ {Af _ {n} } : . | ||
| + | $$ | ||
One constructs the space of test functionals again as the intersection of operator domains: | One constructs the space of test functionals again as the intersection of operator domains: | ||
| − | + | $$ | |
| + | ( {\mathcal S} ) = \lim\limits _ {\vec{p} } ( {\mathcal S} ) _ {p} ,\ \ | ||
| + | ( {\mathcal S} ) _ {p} = D ( \Gamma ( A ^ {p} )) , | ||
| + | $$ | ||
and obtains thus the Gel'fand triple | and obtains thus the Gel'fand triple | ||
| − | + | $$ | |
| + | ( {\mathcal S} ) \subset ( L _ {2} ) \subset ( {\mathcal S} ) ^ {*} . | ||
| + | $$ | ||
| + | |||
| + | Elements of the spaces $ ( {\mathcal S} ) $ | ||
| + | and $ ( {\mathcal S} ) ^ {*} $ | ||
| + | are called Hida test functions (or functionals) and Hida distributions, respectively. | ||
| − | + | ===Properties of $ ( {\mathcal S} ) $=== | |
| + | $ ( {\mathcal S} ) $ | ||
| + | is nuclear (cf. [[Nuclear space]]), and an algebra under [[pointwise multiplication]]; elements of $ ( {\mathcal S} ) $ | ||
| + | have [[Gâteaux derivative]]s | ||
| − | + | $$ | |
| − | + | D _ {h} \phi ( \omega ) = \lim\limits _ {\epsilon \rightarrow 0 } \ | |
| − | + | \frac{1} \epsilon | |
| + | ( \phi ( \omega + h ) - \phi ( \omega ) ) | ||
| + | $$ | ||
| − | in | + | in $ ( {\mathcal S} ) $, |
| + | for any distribution-valued direction $ h \in {\mathcal S} ^ {*} $. | ||
| + | Their images in the Fock space are [[annihilation operators]]. Choosing, in particular, for $ h $ | ||
| + | the Dirac distribution $ \delta _ {t} $, | ||
| + | the corresponding derivative operator is commonly denoted by $ \partial _ {t} $( | ||
| + | Hida derivative), and obeys Boson CCR $ [ \partial _ {t} , \partial _ {s} ] = \delta ( t- s ) $, | ||
| + | as well as $ \omega ( t) = \partial _ {t} + \partial _ {t} ^ {*} $. | ||
| + | The latter relation is the starting point for stochastic integration in the white noise analysis framework [[#References|[a4]]], Chapt. 8. Consider a [[Stochastic integral|stochastic integral]] $ \int dB( t) F $. | ||
| + | Informally, using $ \dot{B} ( t) = \omega ( t) = \partial _ {t} + \partial _ {t} ^ {*} $, | ||
| + | one would obtain | ||
| − | + | $$ | |
| + | \int\limits dB( t) F = \int\limits dt \omega ( t) F = \ | ||
| + | \int\limits dt ( \partial _ {t} + \partial _ {t} ^ {*} ) F. | ||
| + | $$ | ||
| − | In Itô integrals one deals with a forward time differential, hence with | + | In Itô integrals one deals with a forward time differential, hence with $ \partial _ {t+} 0 $ |
| + | acting on a non-anticipating integrand $ F $, | ||
| + | giving zero: $ \int dB( t) F = \int dt \partial _ {t} ^ {*} F $. | ||
| + | This produces not only a viable approach to Itô integration but, more importantly, natural generalizations such as to anticipating integrands [[#References|[a11]]]. Further, $ ( {\mathcal S} ) $ | ||
| + | is Fréchet differentiable (cf. [[Fréchet derivative|Fréchet derivative]]), $ \nabla : ( {\mathcal S} ) \rightarrow {\mathcal S} ( \mathbf R ) \otimes ( {\mathcal S} ) $ | ||
| + | is given by $ ( \nabla \phi )( t, \omega ) = \partial _ {t} \phi ( \omega ) $. | ||
| + | One has $ D _ {h} \phi = \langle h, \nabla \phi \rangle $ | ||
| + | and $ \| \nabla \phi \| _ {L _ {2} } ^ {2} \in ( {\mathcal S} ) $ | ||
| + | for all Hida test functions $ \phi $. | ||
| + | Every Hida test function $ \phi $ | ||
| + | has a version | ||
| − | + | $$ | |
| + | \widetilde \phi ( \omega ) = \sum _ { n } ^ \infty < : \omega ^ \otimes n : , F ^ { ( n) } > , | ||
| + | $$ | ||
| − | with smooth kernels | + | with smooth kernels $ F ^ { ( n) } \in \mathop{\rm Sy} {\mathcal S} ( \mathbf R ^ {n} ) $, |
| + | extending continuously to all $ \omega \in {\mathcal S} ^ {*} ( \mathbf R ) $[[#References|[a12]]]. | ||
| − | The dual space | + | The dual space $ ( {\mathcal S} ) ^ {*} $ |
| + | of Hida distributions has the following properties: all Hida distributions are of finite order ( $ ( {\mathcal S} ) ^ {*} = \cup _ {p=} 1 ^ \infty ( {\mathcal S} ) _ {-} p $); | ||
| + | the $ T $- | ||
| + | and $ S $- | ||
| + | transform extend to $ ( {\mathcal S} ) ^ {*} $, | ||
| + | as application of the distribution $ \Phi $ | ||
| + | to exponential functions which are in $ ( {\mathcal S} ) $: | ||
| + | $ ( T \Phi )( f ) = \langle \Phi , e ^ {iX _ {f} } \rangle $; | ||
| + | any positive Hida distribution $ \Phi $ | ||
| + | is a measure $ v _ \Phi $( | ||
| + | a theorem of Kondrat'ev, Samoilenko and Yokoi, [[#References|[a13]]], [[#References|[a14]]]). | ||
===Examples of Hida distributions.=== | ===Examples of Hida distributions.=== | ||
| − | |||
1) local Wick powers: | 1) local Wick powers: | ||
| − | + | $$ | |
| + | \Phi ( \omega ) = : \omega ^ {n} ( t) : ,\ \ | ||
| + | ( S \Phi )( f ) = f ^ { n } ( t ) . | ||
| + | $$ | ||
| − | 2) Donsker's | + | 2) Donsker's $ \delta $- |
| + | function: | ||
| − | + | $$ | |
| + | \Phi = \delta ( B( t)- a),\ \ | ||
| + | ( S \Phi )( f ) = ( 2 \pi t) ^ {1 / 2 } | ||
| + | e ^ {( F( t)- a) ^ {2} / ( 2t) } , | ||
| + | $$ | ||
| − | with | + | with $ F( t)= \int _ { 0 } ^ { t } f( s) ds $. |
| − | 3) the white noise | + | 3) the white noise $ \delta $- |
| + | function $ \Phi = \delta _ \omega $, | ||
| + | given by | ||
| − | + | $$ | |
| + | \langle \Phi , \phi \rangle = \widetilde \phi ( \omega ) ,\ \ | ||
| + | ( S \Phi )( f ) = e ^ {\langle \omega , f \rangle } C( f ) . | ||
| + | $$ | ||
4) normalized Gaussians: | 4) normalized Gaussians: | ||
| − | + | $$ | |
| + | \Phi ( \omega ) = | ||
| + | \frac{e ^ {\langle \omega , K \omega \rangle } }{ {\mathsf E} ( e ^ {\langle \omega , K \omega \rangle } ) } | ||
| + | ,\ \ | ||
| + | ( S \Phi )( f ) = e ^ {\langle f , ( K /( 1- 2K)) f\rangle } . | ||
| + | $$ | ||
| − | Note that the normalized exponential | + | Note that the normalized exponential $ \Phi ( \omega ) = N \mathop{\rm exp} (\langle \omega , K \omega \rangle) $ |
| + | of example 4) has a well-defined $ S $- | ||
| + | transform for a much larger class of operators $ K $ | ||
| + | than for which the Gaussian and the normalizing constant of the denominator are defined separately. For such $ K $ | ||
| + | one may define $ N \mathop{\rm exp} ( \langle \omega , K \omega \rangle ) $ | ||
| + | by its $ S $- | ||
| + | transform, a fact which is quite often useful in order to describe Hida distributions in terms of their $ S $- | ||
| + | or $ T $- | ||
| + | transform. This is possible because of the following characterization theorem, [[#References|[a15]]]. The following three statements are equivalent: | ||
| − | a) Let | + | a) Let $ F $ |
| + | be a complex-valued functional on the Schwartz space such that, for any $ f \in {\mathcal S} $: | ||
| + | i) $ g( \lambda , f _ {1} ,f _ {2} ) \equiv F( \lambda f _ {1} + f _ {2} ) $ | ||
| + | has an entire analytic extension in $ \lambda $; | ||
| + | and ii) a bound | ||
| − | + | $$ | |
| + | | F( z, f ) | \leq C _ {1} \mathop{\rm exp} ( C _ {2} | z | ^ {2} | ||
| + | \| A ^ {p} f \| _ {2} ^ {2} ) | ||
| + | $$ | ||
| − | holds for some positive | + | holds for some positive $ C _ {i} $ |
| + | and $ p $, | ||
| + | and all complex $ z $. | ||
| − | b) | + | b) $ F $ |
| + | is the $ S $- | ||
| + | transform of a Hida distribution $ \Phi \in ( {\mathcal S} ) ^ {*} $. | ||
| − | c) | + | c) $ F $ |
| + | is the $ T $- | ||
| + | transform of a Hida distribution $ \Phi \in ( {\mathcal S} ) ^ {*} $. | ||
| − | Functionals with the above property a) have been called | + | Functionals with the above property a) have been called $ U $- |
| + | functionals. A corollary to this theorem serves to ensure convergence of sequences of Hida distributions if the corresponding $ U $- | ||
| + | functionals converge uniformly. Analogous theorems have been shown to hold for more general Gaussian systems, covering, in particular, the interesting cases of generalized functions of multi-parameter white noise or of vector-valued Brownian motion [[#References|[a16]]]. Other variants deal with spaces where the growth condition a) ii) for the $ U $- | ||
| + | functionals is relaxed [[#References|[a17]]], [[#References|[a18]]]. | ||
| − | Evidently, the construction of spaces of generalized functions enlarging | + | Evidently, the construction of spaces of generalized functions enlarging $ ( L _ {2} ) $ |
| + | is far from being unique. Other examples are the triple studied by P.A. Meyer [[#References|[a19]]], H. Sugita [[#References|[a21]]], S. Watanabe [[#References|[a20]]] with a large test function space and, consequently, less distributions. Note also the paper of P. Krée in [[#References|[a5]]] for an overview and references to his original work. Conversely, the triple proposed by Meyer and J.-A. Yan [[#References|[a18]]] arrives at a larger distribution space by omitting the growth condition of $ U $- | ||
| + | functionals. An example of a space of test functionals discussed in the context of [[Quantum probability|quantum probability]] is the space $ K = \cap _ {a > 0 } D ( \Gamma ( a \amalg )) $ | ||
| + | of [[#References|[a22]]]. | ||
| − | There are many applications and consequences of the characterization theorem, e.g. | + | There are many applications and consequences of the characterization theorem, e.g. $ \alpha $) |
| + | it is straightforward to verify the $ U $- | ||
| + | functional properties in the examples of $ S $- | ||
| + | transforms given above; the theorem assures immediately that these expressions are indeed $ S $- | ||
| + | transforms of Hida distributions. $ \beta $) | ||
| + | The $ U $- | ||
| + | functionals evidently form an algebra under [[pointwise addition]] and multiplication; this induces two algebraic structures on $ ( {\mathcal S} ) ^ {*} $. | ||
| + | The corresponding products of distributions are convolution (using $ T ^ {-} 1 $), | ||
| + | and the normal ordered product (with $ ( S ^ {-} 1 ) $). | ||
| + | $ \gamma $) | ||
| + | There exists a linear relation between pairs of Hida transformations, through | ||
| − | + | $$ | |
| + | S \Phi = F = T \widehat \Phi . | ||
| + | $$ | ||
| − | If one replaces the white noise measure by a [[Normal distribution|normal distribution]], one finds that | + | If one replaces the white noise measure by a [[Normal distribution|normal distribution]], one finds that $ \widehat \Phi $ |
| + | is nothing but the [[Fourier transform|Fourier transform]] of $ \Phi $. | ||
==The infinite-dimensional Fourier transform.== | ==The infinite-dimensional Fourier transform.== | ||
| − | Cf. [[#References|[a23]]]–[[#References|[a25]]], [[#References|[a4]]], Chapt. 9. The above remark suggests the following definition: For | + | Cf. [[#References|[a23]]]–[[#References|[a25]]], [[#References|[a4]]], Chapt. 9. The above remark suggests the following definition: For $ \Phi \in ( {\mathcal S} ) ^ {*} $ |
| + | one calls $ \widehat \Phi = T ^ {-} 1 S \Phi $ | ||
| + | the Fourier transform of $ \Phi $. | ||
| − | Some examples and properties are as follows. The Fourier transform of | + | Some examples and properties are as follows. The Fourier transform of $ 1 $ |
| + | is the white noise $ \delta $- | ||
| + | function at zero: $ \widehat{1} = \delta _ {0} $, | ||
| + | $ \widehat \delta _ {0} = 1 $. | ||
| + | The Fourier transform intertwines derivative and coordinate multiplications: | ||
| − | + | $$ | |
| + | ( \partial \Phi ) \widehat{ {}} = i \omega \widehat \Phi ,\ \ | ||
| + | ( \omega \Phi ) \widehat{ {}} = i \partial \widehat \Phi . | ||
| + | $$ | ||
| − | This is what singles out | + | This is what singles out $ \Phi \rightarrow \widehat \Phi $ |
| + | as the natural extension of the Fourier transform to infinite dimension: it is (up to constant multiples, of course) the unique continuous linear transformation from $ ( {\mathcal S} ) ^ {*} $ | ||
| + | to itself with this intertwining property [[#References|[a26]]]. | ||
==Dirichlet forms.== | ==Dirichlet forms.== | ||
| − | Cf. [[#References|[a27]]], [[#References|[a28]]], [[#References|[a4]]], Chapt. 10. Recalling that positive Hida distributions are measures, one obtains Dirichlet forms | + | Cf. [[#References|[a27]]], [[#References|[a28]]], [[#References|[a4]]], Chapt. 10. Recalling that positive Hida distributions are measures, one obtains Dirichlet forms $ \epsilon $[[#References|[a29]]]–[[#References|[a31]]] from |
| − | + | $$ | |
| + | \epsilon ( \phi ) = \langle \Phi , | \nabla \phi | ^ {2} \rangle | ||
| + | $$ | ||
| − | for any Hida distribution | + | for any Hida distribution $ \Phi $ |
| + | that is strictly positive (i.e., $ v _ \Phi $ | ||
| + | positive on all open sets) and such that $ \epsilon $ | ||
| + | is closeable on $ L _ {2} ( dv _ \Phi ) $. | ||
| + | For any such $ \Phi $ | ||
| + | one then has in $ L _ {2} ( dv _ \Phi ) $, | ||
| − | + | $$ | |
| + | \overline \epsilon \; ( \phi ) = \| H ^ {1/2} \phi \| ^ {2} , | ||
| + | $$ | ||
| − | where | + | where $ H $ |
| + | is the self-adjoint generator of a Markov semi-group associated with a diffusion process with state space $ {\mathcal S} ^ \prime ( \mathbf R ) $. | ||
==Some applications.== | ==Some applications.== | ||
| − | The above is a direct generalization of the finite-dimensional local Dirichlet forms in [[#References|[a32]]] in terms of quantum-mechanical ground states, which give rise to Schrödinger Hamiltonians | + | The above is a direct generalization of the finite-dimensional local Dirichlet forms in [[#References|[a32]]] in terms of quantum-mechanical ground states, which give rise to Schrödinger Hamiltonians $ H $ |
| + | and to diffusion processes solving non-linear stochastic differential equations. In the present setting one is led to ask the question whether one can describe the ground states of relativistic and Euclidean quantum field theories by (generalized) density functions with respect to the white noise measure $ \mu $, | ||
| + | i.e. via positive $ \Phi \in ( {\mathcal S} ) ^ {*} $, | ||
| + | and whether these then satisfy the above conditions so as to give rise to Dirichlet forms. The first question has been answered, in terms of Fröhlich bounds on the $ n $- | ||
| + | point functions and in terms of the existence of so-called $ \phi $- | ||
| + | bounds [[#References|[a33]]], the second is answered in [[#References|[a34]]], for various models of [[Constructive quantum field theory|constructive quantum field theory]]. | ||
| − | Another fruitful application of white noise analysis in quantum physics is provided by Feynman's path integral. It is well known that the Feynman "integral" is not one with respect to a measure. Hence one cannot hope to interpret it as a weighted average over trajectories, unless one admits distribution-valued weights. A first, still somewhat heuristic, attempt to do so was undertaken in [[#References|[a35]]]. More recently, examples as well as a general criterion were given for which the Feynman integral is indeed the action of a distribution from the space | + | Another fruitful application of white noise analysis in quantum physics is provided by Feynman's path integral. It is well known that the Feynman "integral" is not one with respect to a measure. Hence one cannot hope to interpret it as a weighted average over trajectories, unless one admits distribution-valued weights. A first, still somewhat heuristic, attempt to do so was undertaken in [[#References|[a35]]]. More recently, examples as well as a general criterion were given for which the Feynman integral is indeed the action of a distribution from the space $ ( {\mathcal S} ) ^ {*} $[[#References|[a36]]]. The interest in this approach is essentially twofold: to explore the scope of the method (i.e. the large class of Schrödinger problems that can be solved in this fashion), and to obtain useful quantum-mechanical relationships by manipulating the Feynman integral with the tools of white noise analysis such as, e.g., integration by parts [[#References|[a37]]], [[#References|[a4]]], Chapt. 12. |
For quantum probability in terms of white noise see [[#References|[a38]]]. Hydrodynamic flows in random media are studied in [[#References|[a39]]]. For examples of white noise analysis techniques applied to the solution of stochastic partial differential equations see [[#References|[a40]]], [[#References|[a41]]]. | For quantum probability in terms of white noise see [[#References|[a38]]]. Hydrodynamic flows in random media are studied in [[#References|[a39]]]. For examples of white noise analysis techniques applied to the solution of stochastic partial differential equations see [[#References|[a40]]], [[#References|[a41]]]. | ||
Revision as of 08:29, 6 June 2020
Since its inception in the nineteen seventies [a1]–, white noise analysis has developed into a viable framework for stochastic and infinite-dimensional analysis [a4]–[a6], with a growing number of applications in various disciplines, most notably perhaps in quantum physics. Informally speaking, the role here of (Gaussian, continuous parameter) white noise — a generalized random process (cf. Stochastic process, generalized) with independent values at each point [a7] — is that of an infinite system of coordinates on which to base an infinite-dimensional calculus. More precisely, the starting point is the $ L _ {2} $-
space of the white noise measure, which is then imbedded into Gel'fand triples of test, respectively generalized, function spaces with suitable properties. In particular, the test functions will be chosen sufficiently smooth to admit an infinite-dimensional differential calculus, which is then transported to the generalized functions by duality. With these established, various concepts have natural generalizations to the infinite-dimensional setting. Examples are: the gradient, Laplacian(s) [a4], Chapt. 6, the rotation group [a8], Fourier analysis, and Dirichlet forms. Below some of this is outlined; a comprehensive presentation can be found in [a4].
(Gaussian) white noise.
This is a generalized random process $ \omega $[a1], [a7]; for any Schwartz test function $ f \in {\mathcal S} ( \mathbf R ) $ the "smeared out" process $ \langle \omega , f \rangle $ is a Gaussian random variable $ X _ {f} $ with mean zero and covariance
$$ {\mathsf E} ( X _ {f} X _ {g} ) = \int\limits f( t) g( t) dt = ( f, g) . $$
In terms of the white noise measure $ \mu $ and its characteristic function $ C $, one has
$$ C( f ) = {\mathsf E} ( e ^ {i \langle \omega , f \rangle } ) = \ \int\limits d \mu [ \omega ] e ^ {i \langle \omega , f\rangle } = \ e ^ {- ( 1/2) \int\limits f ^ { 2 } ( t ) dt } , $$
$$ f \in {\mathcal S} ( \mathbf R ) . $$
By extending test functions to $ L _ {2} ( \mathbf R ) $ one obtains a version of Wiener's Brownian motion process $ B ( \cdot ) $ by observing that
$$ B( t) \equiv X( 1 I _ {[ 0, t] } ) = \int\limits _ { 0 } ^ { t } \omega ( \tau ) d \tau $$
expresses the Wiener process in terms of white noise [a1], [a2]. In this sense Brownian functionals can be considered as functionals of white noise. A large collection of the latter is provided by those of finite variance, i.e. by the Hilbert space
$$ ( L _ {2} ) \equiv L _ {2} ( {\mathcal S} ^ {*} ( \mathbf R ) , d \mu ) . $$
The polynomials in $ X _ {f} $, $ f \in {\mathcal S} ( \mathbf R ) $, form a dense subspace in $ ( L _ {2} ) $, hence the monomials $ X _ {f} $ are a total set; to orthogonalize them one introduces the "normal ordered" , or "Wick ordered" or "Hermite" , products
$$ : X _ {f _ {1} } \dots X _ {f _ {n} } : = \ ( 1 - P _ {n-} 1 ) X _ {f _ {1} } \dots X _ {f _ {n} } , $$
where $ P _ {n} $ projects onto the subspace of polynomials of order at most $ n $. They are related to multiple Wiener integrals (cf. Wiener integral) [a9] through
$$ : X _ {f} ^ {n} : = \int\limits f( t _ {1} ) \dots f ( t _ {n} ) \ d B ( t _ {1} ) \dots dB( t _ {n} ) . $$
By linearity and continuity these expressions extend from product kernel functions $ F ^ { ( n) } = \prod f _ {i} $ to symmetric $ L _ {2} $- kernel functions $ F ^ { ( n) } ( t _ {1} \dots t _ {n} ) \in \mathop{\rm Sy} L _ {2} ( \mathbf R ^ {n} ) $; as a result one obtains an isomorphism between the white noise Hilbert space $ ( L _ {2} ) $ and a Boson Fock space
$$ ( L _ {2} ) \simeq \oplus _ { n } \mathop{\rm Sy} L _ {2} ( \mathbf R ^ {n} ,\ n ! dt ) . $$
Another characterization of $ ( L _ {2} ) $ is through the "S-" or "T-transform"
$$ T: \Phi \rightarrow E ( \Phi e ^ {iX _ {f} } ) = ( T \Phi ) ( f ) , $$
$$ S: \Phi \rightarrow E( \Phi [ \cdot + f ]) = ( S \Phi )( f ). $$
They are related through $ ( S \Phi )( f ) = C( f ) \cdot ( T \Phi )(- i f ) = E( \Phi : e ^ {X _ {f} } : ) $.
Generalized functions.
The main interest of the above constructions is to go beyond them, to consider functionals such as e.g. the "action integral" for Brownian motion $ \int : \omega ^ {2} ( t) : dt $; or "Donsker d-functionDonsker's d-function" $ \delta ( B( t) - a) $.
Checking whether their kernel functions are in the Fock space, one finds that in the first example the kernel functions $ F ^ { ( n) } $ are given by $ F ^ { ( n) } ( t _ {1} \dots t _ {n} ) = \delta _ {n ,2 } \delta ( t _ {1} - t _ {2} ) $, which is clearly not square integrable. In the second example the $ F ^ { ( n) } $ are square integrable, but their norms fail to be square summable. Thus, a good extension of $ ( L _ {2} ) $ should be one that relaxes both the $ L _ {2} $- property of the kernel functions and the square summability of their norms.
A standard procedure to enlarge Hilbert spaces is through the construction of Gel'fand triples, such as e.g.
$$ {\mathcal S} ( \mathbf R ) \subset L _ {2} ( \mathbf R ) \subset {\mathcal S} ^ {*} ( \mathbf R ) , $$
with $ {\mathcal S} $ defined as a countable (intersection of) Hilbert space(s):
$$ {\mathcal S} = \cap _ { p= } 1 ^ \infty {\mathcal S} _ {p} ,\ \ {\mathcal S} _ {p} = D( A ^ {p} ) , $$
where $ A $ is the self-adjoint operator $ A = - d ^ {2} / dt ^ {2} + t ^ {2} + 1 $ in $ L _ {2} ( \mathbf R , dt ) $. Here one invokes the second quantization $ \Gamma $[a10] of operators such as $ A $. It is given as a linear operator in $ ( L _ {2} ) $ by its action on normal ordered monomials:
$$ \Gamma ( A) : X _ {f _ {1} } \dots X _ {f _ {1} } : = \ : X _ {A f _ {1} } \dots X _ {Af _ {n} } : . $$
One constructs the space of test functionals again as the intersection of operator domains:
$$ ( {\mathcal S} ) = \lim\limits _ {\vec{p} } ( {\mathcal S} ) _ {p} ,\ \ ( {\mathcal S} ) _ {p} = D ( \Gamma ( A ^ {p} )) , $$
and obtains thus the Gel'fand triple
$$ ( {\mathcal S} ) \subset ( L _ {2} ) \subset ( {\mathcal S} ) ^ {*} . $$
Elements of the spaces $ ( {\mathcal S} ) $ and $ ( {\mathcal S} ) ^ {*} $ are called Hida test functions (or functionals) and Hida distributions, respectively.
Properties of $ ( {\mathcal S} ) $
$ ( {\mathcal S} ) $ is nuclear (cf. Nuclear space), and an algebra under pointwise multiplication; elements of $ ( {\mathcal S} ) $ have Gâteaux derivatives
$$ D _ {h} \phi ( \omega ) = \lim\limits _ {\epsilon \rightarrow 0 } \ \frac{1} \epsilon ( \phi ( \omega + h ) - \phi ( \omega ) ) $$
in $ ( {\mathcal S} ) $, for any distribution-valued direction $ h \in {\mathcal S} ^ {*} $. Their images in the Fock space are annihilation operators. Choosing, in particular, for $ h $ the Dirac distribution $ \delta _ {t} $, the corresponding derivative operator is commonly denoted by $ \partial _ {t} $( Hida derivative), and obeys Boson CCR $ [ \partial _ {t} , \partial _ {s} ] = \delta ( t- s ) $, as well as $ \omega ( t) = \partial _ {t} + \partial _ {t} ^ {*} $. The latter relation is the starting point for stochastic integration in the white noise analysis framework [a4], Chapt. 8. Consider a stochastic integral $ \int dB( t) F $. Informally, using $ \dot{B} ( t) = \omega ( t) = \partial _ {t} + \partial _ {t} ^ {*} $, one would obtain
$$ \int\limits dB( t) F = \int\limits dt \omega ( t) F = \ \int\limits dt ( \partial _ {t} + \partial _ {t} ^ {*} ) F. $$
In Itô integrals one deals with a forward time differential, hence with $ \partial _ {t+} 0 $ acting on a non-anticipating integrand $ F $, giving zero: $ \int dB( t) F = \int dt \partial _ {t} ^ {*} F $. This produces not only a viable approach to Itô integration but, more importantly, natural generalizations such as to anticipating integrands [a11]. Further, $ ( {\mathcal S} ) $ is Fréchet differentiable (cf. Fréchet derivative), $ \nabla : ( {\mathcal S} ) \rightarrow {\mathcal S} ( \mathbf R ) \otimes ( {\mathcal S} ) $ is given by $ ( \nabla \phi )( t, \omega ) = \partial _ {t} \phi ( \omega ) $. One has $ D _ {h} \phi = \langle h, \nabla \phi \rangle $ and $ \| \nabla \phi \| _ {L _ {2} } ^ {2} \in ( {\mathcal S} ) $ for all Hida test functions $ \phi $. Every Hida test function $ \phi $ has a version
$$ \widetilde \phi ( \omega ) = \sum _ { n } ^ \infty < : \omega ^ \otimes n : , F ^ { ( n) } > , $$
with smooth kernels $ F ^ { ( n) } \in \mathop{\rm Sy} {\mathcal S} ( \mathbf R ^ {n} ) $, extending continuously to all $ \omega \in {\mathcal S} ^ {*} ( \mathbf R ) $[a12].
The dual space $ ( {\mathcal S} ) ^ {*} $ of Hida distributions has the following properties: all Hida distributions are of finite order ( $ ( {\mathcal S} ) ^ {*} = \cup _ {p=} 1 ^ \infty ( {\mathcal S} ) _ {-} p $); the $ T $- and $ S $- transform extend to $ ( {\mathcal S} ) ^ {*} $, as application of the distribution $ \Phi $ to exponential functions which are in $ ( {\mathcal S} ) $: $ ( T \Phi )( f ) = \langle \Phi , e ^ {iX _ {f} } \rangle $; any positive Hida distribution $ \Phi $ is a measure $ v _ \Phi $( a theorem of Kondrat'ev, Samoilenko and Yokoi, [a13], [a14]).
Examples of Hida distributions.
1) local Wick powers:
$$ \Phi ( \omega ) = : \omega ^ {n} ( t) : ,\ \ ( S \Phi )( f ) = f ^ { n } ( t ) . $$
2) Donsker's $ \delta $- function:
$$ \Phi = \delta ( B( t)- a),\ \ ( S \Phi )( f ) = ( 2 \pi t) ^ {1 / 2 } e ^ {( F( t)- a) ^ {2} / ( 2t) } , $$
with $ F( t)= \int _ { 0 } ^ { t } f( s) ds $.
3) the white noise $ \delta $- function $ \Phi = \delta _ \omega $, given by
$$ \langle \Phi , \phi \rangle = \widetilde \phi ( \omega ) ,\ \ ( S \Phi )( f ) = e ^ {\langle \omega , f \rangle } C( f ) . $$
4) normalized Gaussians:
$$ \Phi ( \omega ) = \frac{e ^ {\langle \omega , K \omega \rangle } }{ {\mathsf E} ( e ^ {\langle \omega , K \omega \rangle } ) } ,\ \ ( S \Phi )( f ) = e ^ {\langle f , ( K /( 1- 2K)) f\rangle } . $$
Note that the normalized exponential $ \Phi ( \omega ) = N \mathop{\rm exp} (\langle \omega , K \omega \rangle) $ of example 4) has a well-defined $ S $- transform for a much larger class of operators $ K $ than for which the Gaussian and the normalizing constant of the denominator are defined separately. For such $ K $ one may define $ N \mathop{\rm exp} ( \langle \omega , K \omega \rangle ) $ by its $ S $- transform, a fact which is quite often useful in order to describe Hida distributions in terms of their $ S $- or $ T $- transform. This is possible because of the following characterization theorem, [a15]. The following three statements are equivalent:
a) Let $ F $ be a complex-valued functional on the Schwartz space such that, for any $ f \in {\mathcal S} $: i) $ g( \lambda , f _ {1} ,f _ {2} ) \equiv F( \lambda f _ {1} + f _ {2} ) $ has an entire analytic extension in $ \lambda $; and ii) a bound
$$ | F( z, f ) | \leq C _ {1} \mathop{\rm exp} ( C _ {2} | z | ^ {2} \| A ^ {p} f \| _ {2} ^ {2} ) $$
holds for some positive $ C _ {i} $ and $ p $, and all complex $ z $.
b) $ F $ is the $ S $- transform of a Hida distribution $ \Phi \in ( {\mathcal S} ) ^ {*} $.
c) $ F $ is the $ T $- transform of a Hida distribution $ \Phi \in ( {\mathcal S} ) ^ {*} $.
Functionals with the above property a) have been called $ U $- functionals. A corollary to this theorem serves to ensure convergence of sequences of Hida distributions if the corresponding $ U $- functionals converge uniformly. Analogous theorems have been shown to hold for more general Gaussian systems, covering, in particular, the interesting cases of generalized functions of multi-parameter white noise or of vector-valued Brownian motion [a16]. Other variants deal with spaces where the growth condition a) ii) for the $ U $- functionals is relaxed [a17], [a18].
Evidently, the construction of spaces of generalized functions enlarging $ ( L _ {2} ) $ is far from being unique. Other examples are the triple studied by P.A. Meyer [a19], H. Sugita [a21], S. Watanabe [a20] with a large test function space and, consequently, less distributions. Note also the paper of P. Krée in [a5] for an overview and references to his original work. Conversely, the triple proposed by Meyer and J.-A. Yan [a18] arrives at a larger distribution space by omitting the growth condition of $ U $- functionals. An example of a space of test functionals discussed in the context of quantum probability is the space $ K = \cap _ {a > 0 } D ( \Gamma ( a \amalg )) $ of [a22].
There are many applications and consequences of the characterization theorem, e.g. $ \alpha $) it is straightforward to verify the $ U $- functional properties in the examples of $ S $- transforms given above; the theorem assures immediately that these expressions are indeed $ S $- transforms of Hida distributions. $ \beta $) The $ U $- functionals evidently form an algebra under pointwise addition and multiplication; this induces two algebraic structures on $ ( {\mathcal S} ) ^ {*} $. The corresponding products of distributions are convolution (using $ T ^ {-} 1 $), and the normal ordered product (with $ ( S ^ {-} 1 ) $). $ \gamma $) There exists a linear relation between pairs of Hida transformations, through
$$ S \Phi = F = T \widehat \Phi . $$
If one replaces the white noise measure by a normal distribution, one finds that $ \widehat \Phi $ is nothing but the Fourier transform of $ \Phi $.
The infinite-dimensional Fourier transform.
Cf. [a23]–[a25], [a4], Chapt. 9. The above remark suggests the following definition: For $ \Phi \in ( {\mathcal S} ) ^ {*} $ one calls $ \widehat \Phi = T ^ {-} 1 S \Phi $ the Fourier transform of $ \Phi $.
Some examples and properties are as follows. The Fourier transform of $ 1 $ is the white noise $ \delta $- function at zero: $ \widehat{1} = \delta _ {0} $, $ \widehat \delta _ {0} = 1 $. The Fourier transform intertwines derivative and coordinate multiplications:
$$ ( \partial \Phi ) \widehat{ {}} = i \omega \widehat \Phi ,\ \ ( \omega \Phi ) \widehat{ {}} = i \partial \widehat \Phi . $$
This is what singles out $ \Phi \rightarrow \widehat \Phi $ as the natural extension of the Fourier transform to infinite dimension: it is (up to constant multiples, of course) the unique continuous linear transformation from $ ( {\mathcal S} ) ^ {*} $ to itself with this intertwining property [a26].
Dirichlet forms.
Cf. [a27], [a28], [a4], Chapt. 10. Recalling that positive Hida distributions are measures, one obtains Dirichlet forms $ \epsilon $[a29]–[a31] from
$$ \epsilon ( \phi ) = \langle \Phi , | \nabla \phi | ^ {2} \rangle $$
for any Hida distribution $ \Phi $ that is strictly positive (i.e., $ v _ \Phi $ positive on all open sets) and such that $ \epsilon $ is closeable on $ L _ {2} ( dv _ \Phi ) $. For any such $ \Phi $ one then has in $ L _ {2} ( dv _ \Phi ) $,
$$ \overline \epsilon \; ( \phi ) = \| H ^ {1/2} \phi \| ^ {2} , $$
where $ H $ is the self-adjoint generator of a Markov semi-group associated with a diffusion process with state space $ {\mathcal S} ^ \prime ( \mathbf R ) $.
Some applications.
The above is a direct generalization of the finite-dimensional local Dirichlet forms in [a32] in terms of quantum-mechanical ground states, which give rise to Schrödinger Hamiltonians $ H $ and to diffusion processes solving non-linear stochastic differential equations. In the present setting one is led to ask the question whether one can describe the ground states of relativistic and Euclidean quantum field theories by (generalized) density functions with respect to the white noise measure $ \mu $, i.e. via positive $ \Phi \in ( {\mathcal S} ) ^ {*} $, and whether these then satisfy the above conditions so as to give rise to Dirichlet forms. The first question has been answered, in terms of Fröhlich bounds on the $ n $- point functions and in terms of the existence of so-called $ \phi $- bounds [a33], the second is answered in [a34], for various models of constructive quantum field theory.
Another fruitful application of white noise analysis in quantum physics is provided by Feynman's path integral. It is well known that the Feynman "integral" is not one with respect to a measure. Hence one cannot hope to interpret it as a weighted average over trajectories, unless one admits distribution-valued weights. A first, still somewhat heuristic, attempt to do so was undertaken in [a35]. More recently, examples as well as a general criterion were given for which the Feynman integral is indeed the action of a distribution from the space $ ( {\mathcal S} ) ^ {*} $[a36]. The interest in this approach is essentially twofold: to explore the scope of the method (i.e. the large class of Schrödinger problems that can be solved in this fashion), and to obtain useful quantum-mechanical relationships by manipulating the Feynman integral with the tools of white noise analysis such as, e.g., integration by parts [a37], [a4], Chapt. 12.
For quantum probability in terms of white noise see [a38]. Hydrodynamic flows in random media are studied in [a39]. For examples of white noise analysis techniques applied to the solution of stochastic partial differential equations see [a40], [a41].
References
| [a1] | T. Hida, "Stationary stochastic processes" , Princeton Univ. Press (1970) |
| [a2] | T. Hida, "Brownian motion" , Springer (1980) |
| [a3a] | I. Kubo, S. Takenaka, "Calculus on Gaussian white noise I-II" Proc. Japan Acad. , 56 (1980) pp. 376–380; 411–416 |
| [a3b] | I. Kubo, S. Takenaka, "Calculus on Gaussian white noise III" Proc. Japan Acad. , 57 (1981) pp. 433–437 |
| [a3c] | I. Kubo, S. Takenaka, "Calculus on Gaussian white noise IV" Proc. Japan Acad. , 58 (1982) pp. 186–189 |
| [a4] | T. Hida, H.-H. Kuo, J. Potthoff, L. Streit, "White noise - an infinite dimensional calculus" (To appear) |
| [a5] | T. Hida (ed.) H.-H. Kuo (ed.) J. Potthoff (ed.) L. Streid (ed.) , White noise analysis - mathematics and applications , World Sci. (1990) |
| [a6] | H.-H. Kuo, "Lectures on white noise analysis" Soochow Math. J. (1992) |
| [a7] | I.M. Gel'fand, N.Ya. Vilenkin, "Generalized functions. Applications of harmonic analysis" , 4 , Acad. Press (1968) (Translated from Russian) |
| [a8] | T. Hida, "Infinite-dimensional rotation group and unitary group" H. Heyer (ed.) , Probab. Measures on Groups IX Proc. Oberwolfach 17–23 Jan. 1988 , Lect. notes in math. , 1379 , Springer (1989) pp. 125–134 |
| [a9] | K. Ito, "Multiple Wiener integral" J. Math. Soc. Japan , 3 (1951) pp. 157–169 |
| [a10] | B. Simon, "The  Euclidean (quantum) field theory" , Princeton Univ. Press (1974) Euclidean (quantum) field theory" , Princeton Univ. Press (1974) |
| [a11] | J. Asch, J. Potthoff, "Itô's lemma without non-anticipatory conditions" Probab. Th. Rel. Fields , 88 (1991) pp. 17–46 |
| [a12] | I. Kubo, Y. Yokoi, "A remark on the space of testing random variables in the white noise calculus" Nagoya Math. J. , 115 (1989) pp. 139–149 |
| [a13] | Yu.G. [Yu.G. Kondrat'ev] Kondratiev, Yu.S. Samoilenko, "Integral representation of generalized positive definite kernels of an infinite number of variables" Soviet Math. Dokl. , 17 (1976) pp. 517–521 Dokl. Akad. Nauk SSSR , 227 : 4 (1976) pp. 800–803 |
| [a14] | Y. Yokoi, "Positive generalized white noise functionals" Hiroshima Math. J. , 20 (1990) pp. 137–157 |
| [a15] | J. Potthoff, L. Streit, "A characterization of Hida distributions" J. Funkt. Anal. , 101 (1991) pp. 212–229 |
| [a16] | L. Streit, W. Westerkamp, "A generalization of the characterization theorem for generalized functionals of white noise" BiBos Preprint : 480 (1991) |
| [a17] | Yu.G. [Yu.G. Kondrat'ev] Kondratiev, L. Streit, "Spaces of white noise distributions. Constructions, descriptions, applications I" BiBos Preprint : 510 ((To appear in Rep. Math. Phys.)) |
| [a18] | P.A. Meyer, J.-A. Yan, "Les "fonctions caractéristiques" des distributions sur l'espace de Wiener" Univ. Strasbourg Preprint (1991) |
| [a19] | P.A. Meyer, "Quelques résultats analytiques sur le semigroupe d'Ornstein–Uhlenbeck en dimension infinie" , Theory and Application of Random Fields , Springer (1983) pp. 201–214 |
| [a20] | S. Watanabe, "Stochastic differential equations and Malliavin calculus" , Tata Inst. (1984) |
| [a21] | H. Sugita, "Sobolev spaces of Wiener functionals and Malliavin's calculus" J. Math. Kyoto Univ. , 25 (1985) pp. 31–48 |
| [a22] | J.M. Lindsay, H. Maassen, "An integral kernel approach to noise" L. Accardi (ed.) W. von Waldenfels (ed.) , Quantum Probability and Applications III , Lect. notes in math. , 1303 , Springer (1988) pp. 192–208 |
| [a23] | H.-H. Kuo, "The Fourier transform in white noise calculus" J. Multivariate Anal. , 31 (1989) pp. 311–327 |
| [a24] | J.-A. Yan, "An elementary proof of a theorem of Lee" Acta Math. Sci. , 11 : 3 (1991) pp. 356–360 |
| [a25] | Y.-J. Lee, "Analytic version of test functionals, Fourier transform and a characterization of measures in white noise calculus" J. Funct. Anal. , 100 (1991) pp. 359–380 |
| [a26] | T. Hida, H.-H. Kuo, N. Obata, "Transformations for white noise functionals" J. Funct. Anal. (To appear) |
| [a27] | T. Hida, J. Potthoff, L. Streit, "Dirichlet forms and white noise analysis" Comm. Math. Phys. , 116 (1988) pp. 235–245 |
| [a28] | J. Potthoff, M. Röckner, "On the contraction property of energy forms on infinite-dimensional spaces" J. Funct. Anal. , 92 (1990) pp. 155–165 |
| [a29] | M. Fukushima, "Dirichlet forms and Markov processes" , Kodansha & North-Holland (1980) |
| [a30] | S. Kusuoka, "Dirichlet forms and diffusion processes on Banach spaces" J. Fac. Sci. Univ. Tokyo Sect. IA , 29 (1982) pp. 79–95 |
| [a31] | S. Albeverio, M. Röckner, "New developments in the theory and application of Dirichlet forms" S. Albeverio (ed.) et al. (ed.) , Stochastic Processes, Physics and Geometry , World Sci. (1990) pp. 27–76 |
| [a32] | S. Albeverio, R. Hoegh-Krohn, L. Streit, "Energy forms, Hamiltonians and distorted Brownian paths" J. Math. Phys. , 18 (1977) pp. 909–917 |
| [a33] | J. Potthoff, L. Streit, "Invariant states on random and quantum fields: 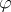 -bounds and white noise analysis" J. Funct. Anal. (To appear) -bounds and white noise analysis" J. Funct. Anal. (To appear) |
| [a34] | S. Albeverio, T. Hida, J. Potthoff, M. Röckner, L. Streit, "Dirichlet forms in terms of white noise analysis: I, II" Rev. Math. Phys. , 1 (1990) pp. 291–312; 313–323 |
| [a35] | T. Hida, L. Streit, "Generalized Brownian functionals and the Feynman integral" Stoch. Proc. Appl. , 16 (1983) pp. 55–69 |
| [a36] | M. de Faria, J. Potthoff, L. Streit, "The Feynman integrand as a Hida distribution" J. Math. Phys. , 32 (1991) pp. 2123–2127 |
| [a37] | D.C. Khandekar, L. Streit, "Constructing the Feynman integrand" Ann. Physik , 1 (1992) pp. 49 |
| [a38] | Zh. Huang, "Quantum white noises - white noise approach to quantum stochastic calculus" Preprint Wuhan University |
| [a39] | T. Lindstrom, B., et al. Oksendal, "Dynamical systems in random media: a white noise functional approach" Preprint, Oslo (1990) |
| [a40] | P.L. Chow, "Generalized solution of some parabolic equations with a random drift" J. Appl. Math. Optimization , 20 (1989) pp. 81–96 |
| [a41] | C. Cochran, J. Potthoff, "Fixed point principles for stochastic partial differential equations" LSU preprint (1992) |
White noise analysis. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=White_noise_analysis&oldid=42896