|
|
| (One intermediate revision by the same user not shown) |
| Line 1: |
Line 1: |
| | + | {{TEX|done}} |
| | An algebraic analogue of the concept of a local Lie group (cf. [[Lie group, local|Lie group, local]]). The theory of formal groups has numerous applications in algebraic geometry, class field theory and cobordism theory. | | An algebraic analogue of the concept of a local Lie group (cf. [[Lie group, local|Lie group, local]]). The theory of formal groups has numerous applications in algebraic geometry, class field theory and cobordism theory. |
| | | | |
| − | A formal group over a field <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f0408201.png" /> is a group object in the category of connected affine formal schemes over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f0408202.png" /> (see [[#References|[1]]], [[#References|[4]]], [[#References|[6]]], [[#References|[7]]]). Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f0408203.png" /> be the functor that associates with an algebra <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f0408204.png" /> the set of algebra homomorphism <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f0408205.png" /> from some Noetherian commutative local <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f0408206.png" />-algebra <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f0408207.png" /> with maximal ideal <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f0408208.png" /> and field of residues <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f0408209.png" />, complete in the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f04082010.png" />-adic topology, such that the homomorphisms map <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f04082011.png" /> into the set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f04082012.png" /> of nilpotent elements of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f04082013.png" />. Then a connected affine formal scheme is a covariant functor <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f04082014.png" /> from the category of finite-dimensional commutative <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f04082015.png" />-algebras <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f04082016.png" /> into the category of sets that is isomorphic to an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f04082017.png" />. That <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f04082018.png" /> is a group object means that there is a group structure given on all the sets <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f04082019.png" /> such that for every <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f04082020.png" />-algebra homomorphism <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f04082021.png" /> the corresponding mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f04082022.png" /> is a group homomorphism. If all the groups <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f04082023.png" /> are commutative, then the formal group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f04082024.png" /> is said to be commutative. Every connected [[Group scheme|group scheme]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f04082025.png" /> over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f04082026.png" /> defines a formal group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f04082027.png" />. Here one can take as <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f04082028.png" /> the completion of the local ring of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f04082029.png" /> at the unit element. | + | A formal group over a field $ k $ |
| | + | is a group object in the category of connected affine formal schemes over $ k $ ( |
| | + | see [[#References|[1]]], [[#References|[4]]], [[#References|[6]]], [[#References|[7]]]). Let $ H _{A} $ |
| | + | be the functor that associates with an algebra $ B $ |
| | + | the set of algebra homomorphism $ A \rightarrow B $ |
| | + | from some Noetherian commutative local $ k $ - |
| | + | algebra $ A $ |
| | + | with maximal ideal $ m $ |
| | + | and field of residues $ k $ , |
| | + | complete in the $ m $ - |
| | + | adic topology, such that the homomorphisms map $ m $ |
| | + | into the set $ \mathop{\rm nil}\nolimits (B) $ |
| | + | of nilpotent elements of $ B $ . |
| | + | Then a connected affine formal scheme is a covariant functor $ H $ |
| | + | from the category of finite-dimensional commutative $ k $ - |
| | + | algebras $ B $ |
| | + | into the category of sets that is isomorphic to an $ H _{A} $ . |
| | + | That $ H $ |
| | + | is a group object means that there is a group structure given on all the sets $ H (B) $ |
| | + | such that for every $ k $ - |
| | + | algebra homomorphism $ B _{1} \rightarrow B _{2} $ |
| | + | the corresponding mapping $ H (B _{1} ) \rightarrow H (B _{2} ) $ |
| | + | is a group homomorphism. If all the groups $ H (B) $ |
| | + | are commutative, then the formal group $ H $ |
| | + | is said to be commutative. Every connected [[Group scheme|group scheme]] $ G $ |
| | + | over $ k $ |
| | + | defines a formal group $ G: \ B \rightarrow G (B) $ . |
| | + | Here one can take as $ A $ |
| | + | the completion of the local ring of $ G $ |
| | + | at the unit element. |
| | | | |
| − | If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f04082030.png" /> is the ring <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f04082031.png" /> of formal power series in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f04082032.png" /> variables over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f04082033.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f04082034.png" /> is called an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f04082036.png" />-dimensional formal Lie group. For a connected [[Algebraic group|algebraic group]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f04082037.png" /> over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f04082038.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f04082039.png" /> is a formal Lie group. A formal Lie group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f04082040.png" /> is isomorphic, as a functor in the category of sets, to the functor <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f04082041.png" /> that associates with an algebra <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f04082042.png" /> the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f04082043.png" />-fold Cartesian product of its nil radical <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f04082044.png" /> with itself. The group structure on the sets <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f04082045.png" /> is given by a formal group law — a collection of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f04082046.png" /> formal power series in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f04082047.png" /> variables <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f04082048.png" />: | + | If $ A $ |
| | + | is the ring $ k [[X _{1} \dots X _{2} ]] $ |
| | + | of formal power series in $ n $ |
| | + | variables over $ k $ , |
| | + | then $ H $ |
| | + | is called an $ n $ - |
| | + | dimensional formal Lie group. For a connected [[Algebraic group|algebraic group]] $ G $ |
| | + | over $ k $ , |
| | + | $ \widehat{G} $ |
| | + | is a formal Lie group. A formal Lie group $ H $ |
| | + | is isomorphic, as a functor in the category of sets, to the functor $ D ^{n} : \ B \rightarrow \mathop{\rm nil}\nolimits (B) ^{n} $ |
| | + | that associates with an algebra $ B $ |
| | + | the $ n $ - |
| | + | fold Cartesian product of its nil radical $ \mathop{\rm nil}\nolimits (B) $ |
| | + | with itself. The group structure on the sets $ H (B) = \mathop{\rm nil}\nolimits (B) ^{n} $ |
| | + | is given by a formal group law — a collection of $ n $ |
| | + | formal power series in $ 2n $ |
| | + | variables $ X _{1} \dots X _{n} ,\ Y _{1} \dots Y _{n} $ : |
| | + | $$ |
| | + | F _{1} (X _{1} \dots X _{n} ,\ Y _{1} \dots Y _{n} ) \dots |
| | + | $$ |
| | + | $$ |
| | + | F _{n} (X _{1} \dots X _{n} ,\ Y _{1} \dots Y _{n} ), |
| | + | $$ |
| | + | satisfying the following conditions:$$ |
| | + | F _{i} (X,\ 0) = X _{i} , |
| | + | F _{i} (0,\ Y) = Y _{i} , |
| | + | $$ |
| | + | $$ |
| | + | F _{i} (X _{1} \dots X _{n} ,\ F _{1} (Y,\ Z) \dots F _{n} (Y,\ Z)) = |
| | + | $$ |
| | + | $$ |
| | + | = |
| | + | F _{i} (F _{1} (X,\ Y) \dots F _{n} (X,\ Y),\ Z _{1} \dots Z _{n} ) . |
| | + | $$ |
| | + | Here $ X = (X _{1} \dots X _{n} ) $ , |
| | + | $ Y = (Y _{1} \dots Y _{n} ), $ |
| | + | $ Z = (Z _{1} \dots Z _{n} ) $ , |
| | + | $ 0 = (0 \dots 0) $ . |
| | + | This group law on the sets $ H (B) = \mathop{\rm nil}\nolimits (B) ^{n} $ |
| | + | is given by the formulas$$ |
| | + | (x _{1} \dots x _{n} ) \circ |
| | + | (y _{1} \dots y _{n} ) = |
| | + | (z _{1} \dots z _{n} ), |
| | + | $$ |
| | + | where $ z _{i} = F _{i} (x _{1} \dots x _{n} ,\ y _{1} \dots y _{n} ) $ ; |
| | + | because $ x $ |
| | + | and $ y $ |
| | + | are nilpotent, all except a finite number of terms of the series are zero. Every formal group law gives group structures on $ \mathop{\rm nil}\nolimits (B) ^{n} $ |
| | + | by means of |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f04082049.png" /></td> </tr></table>
| + | and converts the functor $ D ^{n} $ |
| | + | into a formal Lie group. The concept of a formal group law, and thus of a formal Lie group, can be generalized to the case of arbitrary commutative ground rings (see [[#References|[2]]], [[#References|[5]]]). Sometimes by a formal group one means just a formal Lie group or even a formal group law. |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f04082050.png" /></td> </tr></table>
| + | Just as for local Lie groups (cf. [[Lie group, local|Lie group, local]]) one can define the Lie algebra of a formal Lie group. Over fields $ k $ |
| − | | + | of characteristic 0 the correspondence between a formal Lie group and its Lie algebra defines an equivalence of the respective categories. In characteristic $ p > 0 $ |
| − | satisfying the following conditions:
| + | the situation is more complicated. Thus, over an algebraically closed field (for $ p > 0 $ ) |
| − | | + | there is a countable number of pairwise non-isomorphic one-dimensional commutative formal Lie groups [[#References|[1]]], while all one-dimensional Lie algebras are isomorphic [[#References|[3]]]. Over perfect fields of finite characteristic, commutative formal Lie groups are classified by means of Dieudonné modules (see [[#References|[1]]], [[#References|[6]]]). |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f04082051.png" /></td> </tr></table>
| |
| − | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f04082052.png" /></td> </tr></table>
| |
| − | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f04082053.png" /></td> </tr></table>
| |
| − | | |
| − | Here <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f04082054.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f04082055.png" /> <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f04082056.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f04082057.png" />. This group law on the sets <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f04082058.png" /> is given by the formulas
| |
| − | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f04082059.png" /></td> </tr></table>
| |
| − | | |
| − | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f04082060.png" />; because <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f04082061.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f04082062.png" /> are nilpotent, all except a finite number of terms of the series are zero. Every formal group law gives group structures on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f04082063.png" /> by means of
| |
| − | | |
| − | and converts the functor <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f04082064.png" /> into a formal Lie group. The concept of a formal group law, and thus of a formal Lie group, can be generalized to the case of arbitrary commutative ground rings (see [[#References|[2]]], [[#References|[5]]]). Sometimes by a formal group one means just a formal Lie group or even a formal group law.
| |
| − | | |
| − | Just as for local Lie groups (cf. [[Lie group, local|Lie group, local]]) one can define the Lie algebra of a formal Lie group. Over fields <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f04082065.png" /> of characteristic 0 the correspondence between a formal Lie group and its Lie algebra defines an equivalence of the respective categories. In characteristic <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f04082066.png" /> the situation is more complicated. Thus, over an algebraically closed field (for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f04082067.png" />) there is a countable number of pairwise non-isomorphic one-dimensional commutative formal Lie groups [[#References|[1]]], while all one-dimensional Lie algebras are isomorphic [[#References|[3]]]. Over perfect fields of finite characteristic, commutative formal Lie groups are classified by means of Dieudonné modules (see [[#References|[1]]], [[#References|[6]]]). | |
| | | | |
| | The theory of formal groups over fields can be generalized to the case of arbitrary formal ground schemes [[#References|[7]]]. | | The theory of formal groups over fields can be generalized to the case of arbitrary formal ground schemes [[#References|[7]]]. |
| | | | |
| | ====References==== | | ====References==== |
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> Yu.I. Manin, "The theory of commutative formal groups over fields of finite characteristic" ''Russian Math. Surveys'' , '''18''' (1963) pp. 1–80 ''Uspekhi Mat. Nauk'' , '''18''' : 6 (1963) pp. 3–90</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> R.E. Stong, "Notes on cobordism theory" , Princeton Univ. Press (1968)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> J.-P. Serre, "Lie algebras and Lie groups" , Benjamin (1965) (Translated from French)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> R. Hartshorne, "Algebraic geometry" , Springer (1977)</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> M. Lazard, "Commutative formal groups" , Springer (1975)</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> J.-M. Fontaine, "Groupes <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f04082068.png" />-divisibles sur les corps locaux" ''Astérique'' , '''47–48''' (1977)</TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> B. Mazur, J.T. Tate, "Canonical height pairings via biextensions" J.T. Tate (ed.) M. Artin (ed.) , ''Arithmetic and geometry'' , '''1''' , Birkhäuser (1983) pp. 195–237</TD></TR></table> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> Yu.I. Manin, "The theory of commutative formal groups over fields of finite characteristic" ''Russian Math. Surveys'' , '''18''' (1963) pp. 1–80 ''Uspekhi Mat. Nauk'' , '''18''' : 6 (1963) pp. 3–90 {{MR|157972}} {{ZBL|0128.15603}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> R.E. Stong, "Notes on cobordism theory" , Princeton Univ. Press (1968) {{MR|0248858}} {{ZBL|0181.26604}} </TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> J.-P. Serre, "Lie algebras and Lie groups" , Benjamin (1965) (Translated from French) {{MR|0218496}} {{ZBL|0132.27803}} </TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> R. Hartshorne, "Algebraic geometry" , Springer (1977) {{MR|0463157}} {{ZBL|0367.14001}} </TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> M. Lazard, "Commutative formal groups" , Springer (1975) {{MR|0393050}} {{ZBL|0304.14027}} </TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> J.-M. Fontaine, "Groupes f04082068.png-divisibles sur les corps locaux" ''Astérique'' , '''47–48''' (1977) {{MR|498610}} {{ZBL|}} </TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> B. Mazur, J.T. Tate, "Canonical height pairings via biextensions" J.T. Tate (ed.) M. Artin (ed.) , ''Arithmetic and geometry'' , '''1''' , Birkhäuser (1983) pp. 195–237 {{MR|0717595}} {{ZBL|0574.14036}} </TD></TR></table> |
| | | | |
| | | | |
| | | | |
| | ====Comments==== | | ====Comments==== |
| − | A universal formal group law (for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f04082069.png" />-dimensional formal group laws) is an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f04082070.png" />-dimensional formal group law <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f04082071.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f04082072.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f04082073.png" /> such that for every <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f04082074.png" />-dimensional formal group law <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f04082075.png" /> over a ring <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f04082076.png" /> there is a unique homomorphism of rings <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f04082077.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f04082078.png" />. Here <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f04082079.png" /> denotes the result of applying <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f04082080.png" /> to the coefficients of the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f04082081.png" /> power series <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f04082082.png" />. Universal formal group laws exist and are unique in the sense that if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f04082083.png" /> over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f04082084.png" /> is another one, then there exists a ring isomorphism <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f04082085.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f04082086.png" />. | + | A universal formal group law (for $ n $ - |
| | + | dimensional formal group laws) is an $ n $ - |
| | + | dimensional formal group law $ F _{u} ( X ,\ Y) \in L [ X ,\ Y ] $ , |
| | + | $ X = ( X _{1} \dots X _{n} ) $ , |
| | + | $ Y = ( Y _{1} \dots Y _{n} ) $ |
| | + | such that for every $ n $ - |
| | + | dimensional formal group law $ F ( X ,\ Y ) $ |
| | + | over a ring $ A $ |
| | + | there is a unique homomorphism of rings $ \phi _{F} : \ L \rightarrow A $ |
| | + | such that $ \phi _{F} ^{*} F _{u} ( X ,\ Y ) = F ( X ,\ Y ) $ . |
| | + | Here $ \phi _{F} ^{*} F _{u} ( X ,\ Y ) $ |
| | + | denotes the result of applying $ \phi _{F} ^{*} $ |
| | + | to the coefficients of the $ n $ |
| | + | power series $ F _{u} ( X ,\ Y ) $ . |
| | + | Universal formal group laws exist and are unique in the sense that if $ F _{u} ^ {\ \prime} ( X ,\ Y ) $ |
| | + | over $ L ^ \prime $ |
| | + | is another one, then there exists a ring isomorphism $ \psi : \ L \rightarrow L ^ \prime $ |
| | + | such that $ \psi ^{*} F _{u} ( X ,\ Y ) = F _{u} ^ {\ \prime} ( X ,\ Y ) $ . |
| | | | |
| − | For commutative formal group laws explicit formulas are available for the construction of universal formal group laws, cf. [[#References|[a3]]]. The underlying ring <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f04082087.png" /> is a ring of polynomials in infinitely many indeterminates (Lazard's theorem).
| |
| | | | |
| − | A homomorphism of formal group laws <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f04082088.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f04082089.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f04082090.png" />, is an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f04082091.png" />-tuple of power series in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f04082092.png" />-variables <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f04082093.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f04082094.png" />, such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f04082095.png" />. The homomorphism is an isomorphism if there exists an inverse homomorphism <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f04082096.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f04082097.png" />, and it is a strict isomorphism of formal group laws if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f04082098.png" />(higher order terms).
| + | For commutative formal group laws explicit formulas are available for the construction of universal formal group laws, cf. [[#References|[a3]]]. The underlying ring $ L $ |
| | + | is a ring of polynomials in infinitely many indeterminates (Lazard's theorem). |
| | | | |
| − | Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f04082099.png" /> be a ring of characteristic zero, i.e. the homomorphism of rings <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f040820100.png" /> which sends <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f040820101.png" /> to the unit element in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f040820102.png" /> is injective. Then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f040820103.png" /> is injective. Over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f040820104.png" /> all commutative formal group laws are strictly isomorphic and hence isomorphic to the additive formal group law
| + | A homomorphism of formal group laws $ \alpha : \ F ( X ,\ Y ) \rightarrow G ( X ,\ Y ) $ , |
| | + | $ \mathop{\rm dim}\nolimits \ F = n $ , |
| | + | $ \mathop{\rm dim}\nolimits \ G = m $ , |
| | + | is an $ m $ - |
| | + | tuple of power series in $ n $ - |
| | + | variables $ \alpha ( Z _{1} \dots Z _{n} ) $ , |
| | + | $ \alpha _{i} (0) = 0 $ , |
| | + | such that $ \alpha ( F ( X ,\ Y ) ) = G ( \alpha (X) ,\ \alpha (Y)) $ . |
| | + | The homomorphism is an isomorphism if there exists an inverse homomorphism $ \beta $ |
| | + | such that $ \alpha ( \beta (X) ) = X $ , |
| | + | and it is a strict isomorphism of formal group laws if $ \alpha _{i} (Z) = Z _{i} + $ ( |
| | + | higher order terms). |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f040820105.png" /></td> </tr></table>
| + | Let $ A $ |
| | + | be a ring of characteristic zero, i.e. the homomorphism of rings $ \mathbf Z \rightarrow A $ |
| | + | which sends $ 1 \in \mathbf Z $ |
| | + | to the unit element in $ A $ |
| | + | is injective. Then $ A \rightarrow A \otimes _ {\mathbf Z} \mathbf Q $ |
| | + | is injective. Over $ A \otimes _ {\mathbf Z} \mathbf Q $ |
| | + | all commutative formal group laws are strictly isomorphic and hence isomorphic to the additive formal group law$$ |
| | + | G _{a} ( X ,\ Y ) = ( X _{1} + Y _{1} \dots X _{n} + Y _{n} ) . |
| | + | $$ |
| | + | It follows that for every commutative formal group law $ F ( X ,\ Y ) $ |
| | + | over $ A $ |
| | + | there exists a unique $ n $ - |
| | + | tuple of power series $ f (X) $ , |
| | + | $ f _{i} (X) = X _{i} + \dots $ |
| | + | with coefficients in $ A \otimes _ {\mathbf Z} \mathbf Q $ |
| | + | such that$$ |
| | + | F ( X ,\ Y ) = f ^ {\ -1} ( f (X) + f (Y) ) , |
| | + | $$ |
| | + | where $ f ^ {\ -1} (z) $ |
| | + | is the "inverse function" to $ f (Z) $ , |
| | + | i.e. $ f ^ {\ -1} ( f (Z) ) = Z $ . |
| | + | This $ f (X) $ |
| | + | is called the logarithm of the group law $ F ( X ,\ Y ) $ . |
| | | | |
| − | It follows that for every commutative formal group law <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f040820106.png" /> over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f040820107.png" /> there exists a unique <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f040820108.png" />-tuple of power series <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f040820109.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f040820110.png" /> with coefficients in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f040820111.png" /> such that
| |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f040820112.png" /></td> </tr></table>
| + | The formal group law of complex [[Cobordism|cobordism]] is a universal one-dimensional formal group law (Quillen's theorem) and its logarithm is given by Mishchenko's formula$$ |
| | + | \mathop{\rm log}\nolimits \ F _ {\mathbf M \mathbf U} (X) = |
| | + | \sum _{i=1} ^ \infty |
| | + | i ^{-1} [ \mathbf C \mathbf P ^{i-1} ] |
| | + | X ^{i} . |
| | + | $$ |
| | + | Combined with the explicit construction of a one-dimensional universal group law these facts yield useful information on the generators of the complex cobordism ring $ \mathbf M \mathbf U ^{*} ( \mathop{\rm pt}\nolimits ) $ . |
| | + | Cf. [[Cobordism|Cobordism]] for more details. |
| | | | |
| − | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f040820113.png" /> is the "inverse function" to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f040820114.png" />, i.e. <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f040820115.png" />. This <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f040820116.png" /> is called the logarithm of the group law <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f040820117.png" />.
| + | Let $ F ( X ,\ Y ) $ |
| | + | be an $ n $ - |
| | + | dimensional group law over $ A $ . |
| | + | A curve over $ A $ |
| | + | in $ F $ |
| | + | is an $ n $ - |
| | + | tuple of power series $ \gamma (T) $ |
| | + | in one variable such that $ \gamma (0) = 0 $ . |
| | + | Two curves can be added by $ \gamma (T) + _{F} \delta (T) = F ( \gamma (T) ,\ \delta (T) ) $ . |
| | + | The set of curves is given the natural power series topology and there results a commutative topological group $ {\mathbf C} ( F ; \ A ) $ . |
| | + | The group $ {\mathbf C} ( F ; \ A ) $ |
| | + | admits a number of operators $ V _{n} $ , |
| | + | $ F _{n} $ , |
| | + | $ [a] $ , |
| | + | $ a \in A $ , |
| | + | defined as follows:$$ |
| | + | V _{n} \gamma (T) = \gamma ( T ^{n} ) , |
| | + | $$ |
| | + | $$ |
| | + | [a] \gamma (T) = \gamma ( a T ) , |
| | + | $$ |
| | + | $$ |
| | + | F _{n} \gamma (T) = \gamma ( \zeta _{n} T ^{1}/n ) + _{F} \dots + _{F} \gamma ( \zeta _{n} ^{n} T ^{1}/n ) = {\sum _ |
| | + | i=1 ^ n} {} ^{F} \gamma ( \zeta _{n} ^{i} T ^{1}/n ) , |
| | + | $$ |
| | + | where $ \zeta _{n} $ |
| | + | is a primitive $ n $ - |
| | + | th root of unity. There are a number of relations between these operators and they combine to define a (non-commutative) ring $ \mathop{\rm Cart}\nolimits (A) $ , |
| | + | which generalizes the Dieudonné ring, cf. [[Witt vector|Witt vector]] for the latter. Cartier's second and third theorems on formal group laws say that the $ \mathop{\rm Cart}\nolimits (A) $ |
| | + | modules $ {\mathbf C} ( F ; \ A ) $ |
| | + | classify formal groups and they characterize which groups occur as $ {\mathbf C} ( F ; \ A ) $ ' |
| | + | s. This is the covariant classification of commutative formal groups in contrast with the earlier contravariant classification of commutative formal groups over perfect fields by Dieudonné modules. |
| | | | |
| − | The formal group law of complex [[Cobordism|cobordism]] is a universal one-dimensional formal group law (Quillen's theorem) and its logarithm is given by Mishchenko's formula
| + | Let $ W : \ \mathbf{Rinj} \rightarrow \mathbf{Rinj} $ |
| | + | be the functor of Witt vectors (cf. [[Witt vector|Witt vector]]). Let $ G _{m} ( X ,\ Y ) = X + Y + X Y $ |
| | + | be the (one-dimensional) multiplicative formal group law over $ A $ . |
| | + | Then $ W (A) = {\mathbf C} ( G _{m} ; A ) $ . |
| | + | Cartier's first theorem for formal group laws says that the functor $ F \mapsto {\mathbf C} ( F ; \ A ) $ |
| | + | is representable. More precisely, let $ \widehat{W} $ |
| | + | be the (infinite-dimensional) formal group law given by the addition formulas of the Witt vectors and let $ \gamma _{0} (T) $ |
| | + | be the curve $ (T ,\ 0 ,\ 0 ,\dots ) $ . |
| | + | Then for every formal group law $ F ( X ,\ Y ) $ |
| | + | and curve $ \gamma (T) \in {\mathbf C} ( F ; \ A ) $ |
| | + | there is unique homomorphism of formal group laws $ \alpha _ \gamma : \ \widehat{W} \rightarrow F $ |
| | + | such that $ \alpha _ \gamma ( \gamma _{0} (T) ) = \gamma (T) $ . |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f040820118.png" /></td> </tr></table>
| |
| | | | |
| − | Combined with the explicit construction of a one-dimensional universal group law these facts yield useful information on the generators of the complex cobordism ring <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f040820119.png" />. Cf. [[Cobordism|Cobordism]] for more details.
| + | There exists a Pontryagin-type duality between commutative formal groups and commutative affine (algebraic) groups over a field $ k $ , |
| | + | called Cartier duality. Cf. [[#References|[a3]]], [[#References|[a4]]] for more details. Correspondingly, Dieudonné modules are also important in the classification of commutative affine (algebraic) groups. Essentially, Cartier duality comes from the "duality" between algebras and co-algebras; cf. [[Co-algebra|Co-algebra]]. |
| | | | |
| − | Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f040820120.png" /> be an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f040820121.png" />-dimensional group law over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f040820122.png" />. A curve over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f040820123.png" /> in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f040820124.png" /> is an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f040820125.png" />-tuple of power series <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f040820126.png" /> in one variable such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f040820127.png" />. Two curves can be added by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f040820128.png" />. The set of curves is given the natural power series topology and there results a commutative topological group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f040820129.png" />. The group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f040820130.png" /> admits a number of operators <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f040820131.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f040820132.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f040820133.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f040820134.png" />, defined as follows: | + | Let $ A $ |
| | + | be a discrete valuation ring with finite residue field $ k $ |
| | + | and maximal ideal $ \mathfrak m = ( \pi ) $ . |
| | + | The Lubin–Tate formal group law associated to $ ( A ,\ \pi ) $ |
| | + | is defined by the logarithm$$ |
| | + | f _ \pi (X) = X + \pi ^{-1} X ^{q} + \pi ^{-2} X ^ {q ^{2}} + \dots . |
| | + | $$ |
| | + | Then $ F _ \pi ( X ,\ Y ) = f _ \pi ^ {\ -1} ( f _ \pi (X) + f _ \pi (Y) ) $ |
| | + | has its coefficients in $ A $ . |
| | + | These formal group laws are in a sense formal $ p $ - |
| | + | adic analogues of elliptic curves with complex multiplication in that they have maximally large endomorphism rings. They are also analogues in the role they play vis à vis the class field theory of $ K $ , |
| | + | the quotient field of $ A $ . |
| | + | Indeed, let $ F _ \pi ( \bar{\mathfrak m} ) $ |
| | + | be the set $ \bar{\mathfrak m} $ |
| | + | with the addition $ a + b = F _ \pi ( a ,\ b ) $ . |
| | + | Here $ \bar{\mathfrak m} $ |
| | + | is the maximal ideal of the ring of integers of an algebraic closure of $ K $ . |
| | + | Then a maximal Abelian totally ramified extension of $ K $ |
| | + | is generated by the torsion elements of $ F ( \bar{\mathfrak m} ) $ ; |
| | + | cf. [[#References|[a3]]], [[#References|[a5]]] for more details. |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f040820135.png" /></td> </tr></table>
| + | Formal groups also are an important tool in algebraic geometry, especially in the theory of Abelian varieties. This holds even more so for a generalization: $ p $ - |
| − | | + | divisible groups; cf. [[P-divisible group|$ p $ - |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f040820136.png" /></td> </tr></table>
| + | divisible group]]. |
| − | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f040820137.png" /></td> </tr></table>
| |
| − | | |
| − | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f040820138.png" /> is a primitive <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f040820139.png" />-th root of unity. There are a number of relations between these operators and they combine to define a (non-commutative) ring <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f040820140.png" />, which generalizes the Dieudonné ring, cf. [[Witt vector|Witt vector]] for the latter. Cartier's second and third theorems on formal group laws say that the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f040820141.png" /> modules <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f040820142.png" /> classify formal groups and they characterize which groups occur as <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f040820143.png" />'s. This is the covariant classification of commutative formal groups in contrast with the earlier contravariant classification of commutative formal groups over perfect fields by Dieudonné modules.
| |
| − | | |
| − | Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f040820144.png" /> be the functor of Witt vectors (cf. [[Witt vector|Witt vector]]). Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f040820145.png" /> be the (one-dimensional) multiplicative formal group law over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f040820146.png" />. Then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f040820147.png" />. Cartier's first theorem for formal group laws says that the functor <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f040820148.png" /> is representable. More precisely, let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f040820149.png" /> be the (infinite-dimensional) formal group law given by the addition formulas of the Witt vectors and let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f040820150.png" /> be the curve <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f040820151.png" />. Then for every formal group law <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f040820152.png" /> and curve <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f040820153.png" /> there is unique homomorphism of formal group laws <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f040820154.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f040820155.png" />.
| |
| − | | |
| − | There exists a Pontryagin-type duality between commutative formal groups and commutative affine (algebraic) groups over a field <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f040820156.png" />, called Cartier duality. Cf. [[#References|[a3]]], [[#References|[a4]]] for more details. Correspondingly, Dieudonné modules are also important in the classification of commutative affine (algebraic) groups. Essentially, Cartier duality comes from the "duality" between algebras and co-algebras; cf. [[Co-algebra|Co-algebra]].
| |
| − | | |
| − | Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f040820157.png" /> be a discrete valuation ring with finite residue field <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f040820158.png" /> and maximal ideal <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f040820159.png" />. The Lubin–Tate formal group law associated to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f040820160.png" /> is defined by the logarithm
| |
| − | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f040820161.png" /></td> </tr></table>
| |
| − | | |
| − | Then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f040820162.png" /> has its coefficients in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f040820163.png" />. These formal group laws are in a sense formal <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f040820164.png" />-adic analogues of elliptic curves with complex multiplication in that they have maximally large endomorphism rings. They are also analogues in the role they play vis à vis the class field theory of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f040820165.png" />, the quotient field of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f040820166.png" />. Indeed, let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f040820167.png" /> be the set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f040820168.png" /> with the addition <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f040820169.png" />. Here <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f040820170.png" /> is the maximal ideal of the ring of integers of an algebraic closure of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f040820171.png" />. Then a maximal Abelian totally ramified extension of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f040820172.png" /> is generated by the torsion elements of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f040820173.png" />; cf. [[#References|[a3]]], [[#References|[a5]]] for more details.
| |
| − | | |
| − | Formal groups also are an important tool in algebraic geometry, especially in the theory of Abelian varieties. This holds even more so for a generalization: <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f040820174.png" />-divisible groups; cf. [[P-divisible group|<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f040820175.png" />-divisible group]]. | |
| | | | |
| | Lazard's theorem on one-dimensional formal group laws says that all one-dimensional formal group laws over a ring without nilpotents are commutative. | | Lazard's theorem on one-dimensional formal group laws says that all one-dimensional formal group laws over a ring without nilpotents are commutative. |
| | | | |
| − | Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f040820176.png" /> be a one-dimensional formal group law. Define inductively <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f040820177.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f040820178.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f040820179.png" />. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f040820180.png" /> be defined over a field <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f040820181.png" /> of characteristic <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f040820182.png" />. Then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f040820183.png" /> is necessarily of the form <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f040820184.png" /> (higher degree terms) or is equal to zero. The positive integer <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f040820185.png" /> is called the height of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f040820186.png" />; if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f040820187.png" />, the height of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f040820188.png" /> is taken to be <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f040820189.png" />. Over an algebraically closed field of characteristic <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f040820190.png" /> the one-dimensional formal group laws are classified by their heights, and all heights <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f040820191.png" /> occur. | + | Let $ F ( X ,\ Y ) $ |
| − | | + | be a one-dimensional formal group law. Define inductively $ [n] (X) = F ( X ,\ [ n - 1 ] (X) ) $ , |
| − | Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f040820192.png" /> be a one-dimensional formal group law over a ring <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f040820193.png" /> in which every prime number except <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f040820194.png" /> is invertible, e.g. <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f040820195.png" /> is the ring of integers of a local field of residue characteristic <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f040820196.png" /> or <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f040820197.png" /> is a field of characteristic <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f040820198.png" />. Assume for the moment that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f040820199.png" /> is of characteristic zero and let
| + | $ n \geq 2 $ , |
| − | | + | $ [1] (X) = X $ . |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f040820200.png" /></td> </tr></table>
| + | Let $ F $ |
| − | | + | be defined over a field $ k $ |
| − | be the logarithm of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f040820201.png" />. Then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f040820202.png" /> is strictly isomorphic over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f040820203.png" /> to the formal group law <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f040820204.png" /> whose logarithm is equal to
| + | of characteristic $ p > 0 $ . |
| | + | Then $ [p] (X) $ |
| | + | is necessarily of the form $ X ^ {p ^{h}} + $ ( |
| | + | higher degree terms) or is equal to zero. The positive integer $ h $ |
| | + | is called the height of $ F $ ; |
| | + | if $ [p] (X) = 0 $ , |
| | + | the height of $ F $ |
| | + | is taken to be $ \infty $ . |
| | + | Over an algebraically closed field of characteristic $ p > 0 $ |
| | + | the one-dimensional formal group laws are classified by their heights, and all heights $ 1 ,\ 2 \dots \infty $ |
| | + | occur. |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f040820205.png" /></td> </tr></table>
| + | Let $ F ( X ,\ Y ) $ |
| | + | be a one-dimensional formal group law over a ring $ A $ |
| | + | in which every prime number except $ p $ |
| | + | is invertible, e.g. $ A $ |
| | + | is the ring of integers of a local field of residue characteristic $ p $ |
| | + | or $ A $ |
| | + | is a field of characteristic $ p $ . |
| | + | Assume for the moment that $ A $ |
| | + | is of characteristic zero and let$$ |
| | + | f (X) = X + a _{2} X ^{2} + a _{3} X ^{3} + \dots |
| | + | $$ |
| | + | be the logarithm of $ F ( X ,\ Y ) $ . |
| | + | Then $ F ( X ,\ Y ) $ |
| | + | is strictly isomorphic over $ A $ |
| | + | to the formal group law $ F _{(p)} ( X ,\ Y ) $ |
| | + | whose logarithm is equal to$$ |
| | + | f _{(p)} (X) = X + a _{p} X ^{p} + a _ {p ^{2}} X ^ {p ^{2}} + \dots . |
| | + | $$ |
| | + | The result extends to the case that $ A $ |
| | + | is not of characteristic zero and to more-dimensional commutative formal group laws. $ F _{(p)} ( X ,\ Y) $ |
| | + | is called the $ p $ - |
| | + | typification of $ F ( X ,\ Y ) $ . |
| | | | |
| − | The result extends to the case that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f040820206.png" /> is not of characteristic zero and to more-dimensional commutative formal group laws. <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f040820207.png" /> is called the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f040820209.png" />-typification of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f040820210.png" />.
| |
| | | | |
| | ====References==== | | ====References==== |
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> J.T. Tate, "<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f040820211.png" />-divisible groups" T.A. Springer (ed.) et al. (ed.) , ''Proc. Conf. local fields (Driebergen, 1966)'' , Springer (1967) pp. 158–183</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> J.-P. Serre, "Groupes <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f040820212.png" />-divisible (d' après J. Tate)" ''Sem. Bourbaki'' , '''19, Exp. 318''' (1966–1967)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> M. Hazewinkel, "Formal groups and applications" , Acad. Press (1978)</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> M. Demazure, P. Gabriel, "Groupes algébriques" , '''1''' , Masson & North-Holland (1970)</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> J. Lubin, J. Tate, "Formal complex multiplication in local fields" ''Ann. of Math.'' , '''81''' (1965) pp. 380–387</TD></TR></table> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> J.T. Tate, "<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f040820211.png" />-divisible groups" T.A. Springer (ed.) et al. (ed.) , ''Proc. Conf. local fields (Driebergen, 1966)'' , Springer (1967) pp. 158–183 {{MR|0231827}} {{ZBL|0157.27601}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> J.-P. Serre, "Groupes <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f040820212.png" />-divisible (d' après J. Tate)" ''Sem. Bourbaki'' , '''19, Exp. 318''' (1966–1967) {{MR|1610452}} {{MR|0393040}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> M. Hazewinkel, "Formal groups and applications" , Acad. Press (1978) {{MR|0506881}} {{MR|0463184}} {{ZBL|0454.14020}} </TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> M. Demazure, P. Gabriel, "Groupes algébriques" , '''1''' , Masson & North-Holland (1970) {{MR|0302656}} {{MR|0284446}} {{ZBL|0223.14009}} {{ZBL|0203.23401}} </TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> J. Lubin, J. Tate, "Formal complex multiplication in local fields" ''Ann. of Math.'' , '''81''' (1965) pp. 380–387 {{MR|0172878}} {{ZBL|0128.26501}} </TD></TR></table> |
An algebraic analogue of the concept of a local Lie group (cf. Lie group, local). The theory of formal groups has numerous applications in algebraic geometry, class field theory and cobordism theory.
A formal group over a field $ k $
is a group object in the category of connected affine formal schemes over $ k $ (
see [1], [4], [6], [7]). Let $ H _{A} $
be the functor that associates with an algebra $ B $
the set of algebra homomorphism $ A \rightarrow B $
from some Noetherian commutative local $ k $ -
algebra $ A $
with maximal ideal $ m $
and field of residues $ k $ ,
complete in the $ m $ -
adic topology, such that the homomorphisms map $ m $
into the set $ \mathop{\rm nil}\nolimits (B) $
of nilpotent elements of $ B $ .
Then a connected affine formal scheme is a covariant functor $ H $
from the category of finite-dimensional commutative $ k $ -
algebras $ B $
into the category of sets that is isomorphic to an $ H _{A} $ .
That $ H $
is a group object means that there is a group structure given on all the sets $ H (B) $
such that for every $ k $ -
algebra homomorphism $ B _{1} \rightarrow B _{2} $
the corresponding mapping $ H (B _{1} ) \rightarrow H (B _{2} ) $
is a group homomorphism. If all the groups $ H (B) $
are commutative, then the formal group $ H $
is said to be commutative. Every connected group scheme $ G $
over $ k $
defines a formal group $ G: \ B \rightarrow G (B) $ .
Here one can take as $ A $
the completion of the local ring of $ G $
at the unit element.
If $ A $
is the ring $ k [[X _{1} \dots X _{2} ]] $
of formal power series in $ n $
variables over $ k $ ,
then $ H $
is called an $ n $ -
dimensional formal Lie group. For a connected algebraic group $ G $
over $ k $ ,
$ \widehat{G} $
is a formal Lie group. A formal Lie group $ H $
is isomorphic, as a functor in the category of sets, to the functor $ D ^{n} : \ B \rightarrow \mathop{\rm nil}\nolimits (B) ^{n} $
that associates with an algebra $ B $
the $ n $ -
fold Cartesian product of its nil radical $ \mathop{\rm nil}\nolimits (B) $
with itself. The group structure on the sets $ H (B) = \mathop{\rm nil}\nolimits (B) ^{n} $
is given by a formal group law — a collection of $ n $
formal power series in $ 2n $
variables $ X _{1} \dots X _{n} ,\ Y _{1} \dots Y _{n} $ :
$$
F _{1} (X _{1} \dots X _{n} ,\ Y _{1} \dots Y _{n} ) \dots
$$
$$
F _{n} (X _{1} \dots X _{n} ,\ Y _{1} \dots Y _{n} ),
$$
satisfying the following conditions:$$
F _{i} (X,\ 0) = X _{i} ,
F _{i} (0,\ Y) = Y _{i} ,
$$
$$
F _{i} (X _{1} \dots X _{n} ,\ F _{1} (Y,\ Z) \dots F _{n} (Y,\ Z)) =
$$
$$
=
F _{i} (F _{1} (X,\ Y) \dots F _{n} (X,\ Y),\ Z _{1} \dots Z _{n} ) .
$$
Here $ X = (X _{1} \dots X _{n} ) $ ,
$ Y = (Y _{1} \dots Y _{n} ), $
$ Z = (Z _{1} \dots Z _{n} ) $ ,
$ 0 = (0 \dots 0) $ .
This group law on the sets $ H (B) = \mathop{\rm nil}\nolimits (B) ^{n} $
is given by the formulas$$
(x _{1} \dots x _{n} ) \circ
(y _{1} \dots y _{n} ) =
(z _{1} \dots z _{n} ),
$$
where $ z _{i} = F _{i} (x _{1} \dots x _{n} ,\ y _{1} \dots y _{n} ) $ ;
because $ x $
and $ y $
are nilpotent, all except a finite number of terms of the series are zero. Every formal group law gives group structures on $ \mathop{\rm nil}\nolimits (B) ^{n} $
by means of
and converts the functor $ D ^{n} $
into a formal Lie group. The concept of a formal group law, and thus of a formal Lie group, can be generalized to the case of arbitrary commutative ground rings (see [2], [5]). Sometimes by a formal group one means just a formal Lie group or even a formal group law.
Just as for local Lie groups (cf. Lie group, local) one can define the Lie algebra of a formal Lie group. Over fields $ k $
of characteristic 0 the correspondence between a formal Lie group and its Lie algebra defines an equivalence of the respective categories. In characteristic $ p > 0 $
the situation is more complicated. Thus, over an algebraically closed field (for $ p > 0 $ )
there is a countable number of pairwise non-isomorphic one-dimensional commutative formal Lie groups [1], while all one-dimensional Lie algebras are isomorphic [3]. Over perfect fields of finite characteristic, commutative formal Lie groups are classified by means of Dieudonné modules (see [1], [6]).
The theory of formal groups over fields can be generalized to the case of arbitrary formal ground schemes [7].
References
| [1] | Yu.I. Manin, "The theory of commutative formal groups over fields of finite characteristic" Russian Math. Surveys , 18 (1963) pp. 1–80 Uspekhi Mat. Nauk , 18 : 6 (1963) pp. 3–90 MR157972 Zbl 0128.15603 |
| [2] | R.E. Stong, "Notes on cobordism theory" , Princeton Univ. Press (1968) MR0248858 Zbl 0181.26604 |
| [3] | J.-P. Serre, "Lie algebras and Lie groups" , Benjamin (1965) (Translated from French) MR0218496 Zbl 0132.27803 |
| [4] | R. Hartshorne, "Algebraic geometry" , Springer (1977) MR0463157 Zbl 0367.14001 |
| [5] | M. Lazard, "Commutative formal groups" , Springer (1975) MR0393050 Zbl 0304.14027 |
| [6] | J.-M. Fontaine, "Groupes f04082068.png-divisibles sur les corps locaux" Astérique , 47–48 (1977) MR498610 |
| [7] | B. Mazur, J.T. Tate, "Canonical height pairings via biextensions" J.T. Tate (ed.) M. Artin (ed.) , Arithmetic and geometry , 1 , Birkhäuser (1983) pp. 195–237 MR0717595 Zbl 0574.14036 |
A universal formal group law (for $ n $ -
dimensional formal group laws) is an $ n $ -
dimensional formal group law $ F _{u} ( X ,\ Y) \in L [ X ,\ Y ] $ ,
$ X = ( X _{1} \dots X _{n} ) $ ,
$ Y = ( Y _{1} \dots Y _{n} ) $
such that for every $ n $ -
dimensional formal group law $ F ( X ,\ Y ) $
over a ring $ A $
there is a unique homomorphism of rings $ \phi _{F} : \ L \rightarrow A $
such that $ \phi _{F} ^{*} F _{u} ( X ,\ Y ) = F ( X ,\ Y ) $ .
Here $ \phi _{F} ^{*} F _{u} ( X ,\ Y ) $
denotes the result of applying $ \phi _{F} ^{*} $
to the coefficients of the $ n $
power series $ F _{u} ( X ,\ Y ) $ .
Universal formal group laws exist and are unique in the sense that if $ F _{u} ^ {\ \prime} ( X ,\ Y ) $
over $ L ^ \prime $
is another one, then there exists a ring isomorphism $ \psi : \ L \rightarrow L ^ \prime $
such that $ \psi ^{*} F _{u} ( X ,\ Y ) = F _{u} ^ {\ \prime} ( X ,\ Y ) $ .
For commutative formal group laws explicit formulas are available for the construction of universal formal group laws, cf. [a3]. The underlying ring $ L $
is a ring of polynomials in infinitely many indeterminates (Lazard's theorem).
A homomorphism of formal group laws $ \alpha : \ F ( X ,\ Y ) \rightarrow G ( X ,\ Y ) $ ,
$ \mathop{\rm dim}\nolimits \ F = n $ ,
$ \mathop{\rm dim}\nolimits \ G = m $ ,
is an $ m $ -
tuple of power series in $ n $ -
variables $ \alpha ( Z _{1} \dots Z _{n} ) $ ,
$ \alpha _{i} (0) = 0 $ ,
such that $ \alpha ( F ( X ,\ Y ) ) = G ( \alpha (X) ,\ \alpha (Y)) $ .
The homomorphism is an isomorphism if there exists an inverse homomorphism $ \beta $
such that $ \alpha ( \beta (X) ) = X $ ,
and it is a strict isomorphism of formal group laws if $ \alpha _{i} (Z) = Z _{i} + $ (
higher order terms).
Let $ A $
be a ring of characteristic zero, i.e. the homomorphism of rings $ \mathbf Z \rightarrow A $
which sends $ 1 \in \mathbf Z $
to the unit element in $ A $
is injective. Then $ A \rightarrow A \otimes _ {\mathbf Z} \mathbf Q $
is injective. Over $ A \otimes _ {\mathbf Z} \mathbf Q $
all commutative formal group laws are strictly isomorphic and hence isomorphic to the additive formal group law$$
G _{a} ( X ,\ Y ) = ( X _{1} + Y _{1} \dots X _{n} + Y _{n} ) .
$$
It follows that for every commutative formal group law $ F ( X ,\ Y ) $
over $ A $
there exists a unique $ n $ -
tuple of power series $ f (X) $ ,
$ f _{i} (X) = X _{i} + \dots $
with coefficients in $ A \otimes _ {\mathbf Z} \mathbf Q $
such that$$
F ( X ,\ Y ) = f ^ {\ -1} ( f (X) + f (Y) ) ,
$$
where $ f ^ {\ -1} (z) $
is the "inverse function" to $ f (Z) $ ,
i.e. $ f ^ {\ -1} ( f (Z) ) = Z $ .
This $ f (X) $
is called the logarithm of the group law $ F ( X ,\ Y ) $ .
The formal group law of complex cobordism is a universal one-dimensional formal group law (Quillen's theorem) and its logarithm is given by Mishchenko's formula$$
\mathop{\rm log}\nolimits \ F _ {\mathbf M \mathbf U} (X) =
\sum _{i=1} ^ \infty
i ^{-1} [ \mathbf C \mathbf P ^{i-1} ]
X ^{i} .
$$
Combined with the explicit construction of a one-dimensional universal group law these facts yield useful information on the generators of the complex cobordism ring $ \mathbf M \mathbf U ^{*} ( \mathop{\rm pt}\nolimits ) $ .
Cf. Cobordism for more details.
Let $ F ( X ,\ Y ) $
be an $ n $ -
dimensional group law over $ A $ .
A curve over $ A $
in $ F $
is an $ n $ -
tuple of power series $ \gamma (T) $
in one variable such that $ \gamma (0) = 0 $ .
Two curves can be added by $ \gamma (T) + _{F} \delta (T) = F ( \gamma (T) ,\ \delta (T) ) $ .
The set of curves is given the natural power series topology and there results a commutative topological group $ {\mathbf C} ( F ; \ A ) $ .
The group $ {\mathbf C} ( F ; \ A ) $
admits a number of operators $ V _{n} $ ,
$ F _{n} $ ,
$ [a] $ ,
$ a \in A $ ,
defined as follows:$$
V _{n} \gamma (T) = \gamma ( T ^{n} ) ,
$$
$$
[a] \gamma (T) = \gamma ( a T ) ,
$$
$$
F _{n} \gamma (T) = \gamma ( \zeta _{n} T ^{1}/n ) + _{F} \dots + _{F} \gamma ( \zeta _{n} ^{n} T ^{1}/n ) = {\sum _
i=1 ^ n} {} ^{F} \gamma ( \zeta _{n} ^{i} T ^{1}/n ) ,
$$
where $ \zeta _{n} $
is a primitive $ n $ -
th root of unity. There are a number of relations between these operators and they combine to define a (non-commutative) ring $ \mathop{\rm Cart}\nolimits (A) $ ,
which generalizes the Dieudonné ring, cf. Witt vector for the latter. Cartier's second and third theorems on formal group laws say that the $ \mathop{\rm Cart}\nolimits (A) $
modules $ {\mathbf C} ( F ; \ A ) $
classify formal groups and they characterize which groups occur as $ {\mathbf C} ( F ; \ A ) $ '
s. This is the covariant classification of commutative formal groups in contrast with the earlier contravariant classification of commutative formal groups over perfect fields by Dieudonné modules.
Let $ W : \ \mathbf{Rinj} \rightarrow \mathbf{Rinj} $
be the functor of Witt vectors (cf. Witt vector). Let $ G _{m} ( X ,\ Y ) = X + Y + X Y $
be the (one-dimensional) multiplicative formal group law over $ A $ .
Then $ W (A) = {\mathbf C} ( G _{m} ; A ) $ .
Cartier's first theorem for formal group laws says that the functor $ F \mapsto {\mathbf C} ( F ; \ A ) $
is representable. More precisely, let $ \widehat{W} $
be the (infinite-dimensional) formal group law given by the addition formulas of the Witt vectors and let $ \gamma _{0} (T) $
be the curve $ (T ,\ 0 ,\ 0 ,\dots ) $ .
Then for every formal group law $ F ( X ,\ Y ) $
and curve $ \gamma (T) \in {\mathbf C} ( F ; \ A ) $
there is unique homomorphism of formal group laws $ \alpha _ \gamma : \ \widehat{W} \rightarrow F $
such that $ \alpha _ \gamma ( \gamma _{0} (T) ) = \gamma (T) $ .
There exists a Pontryagin-type duality between commutative formal groups and commutative affine (algebraic) groups over a field $ k $ ,
called Cartier duality. Cf. [a3], [a4] for more details. Correspondingly, Dieudonné modules are also important in the classification of commutative affine (algebraic) groups. Essentially, Cartier duality comes from the "duality" between algebras and co-algebras; cf. Co-algebra.
Let $ A $
be a discrete valuation ring with finite residue field $ k $
and maximal ideal $ \mathfrak m = ( \pi ) $ .
The Lubin–Tate formal group law associated to $ ( A ,\ \pi ) $
is defined by the logarithm$$
f _ \pi (X) = X + \pi ^{-1} X ^{q} + \pi ^{-2} X ^ {q ^{2}} + \dots .
$$
Then $ F _ \pi ( X ,\ Y ) = f _ \pi ^ {\ -1} ( f _ \pi (X) + f _ \pi (Y) ) $
has its coefficients in $ A $ .
These formal group laws are in a sense formal $ p $ -
adic analogues of elliptic curves with complex multiplication in that they have maximally large endomorphism rings. They are also analogues in the role they play vis à vis the class field theory of $ K $ ,
the quotient field of $ A $ .
Indeed, let $ F _ \pi ( \bar{\mathfrak m} ) $
be the set $ \bar{\mathfrak m} $
with the addition $ a + b = F _ \pi ( a ,\ b ) $ .
Here $ \bar{\mathfrak m} $
is the maximal ideal of the ring of integers of an algebraic closure of $ K $ .
Then a maximal Abelian totally ramified extension of $ K $
is generated by the torsion elements of $ F ( \bar{\mathfrak m} ) $ ;
cf. [a3], [a5] for more details.
Formal groups also are an important tool in algebraic geometry, especially in the theory of Abelian varieties. This holds even more so for a generalization: $ p $ -
divisible groups; cf. $ p $ -
divisible group.
Lazard's theorem on one-dimensional formal group laws says that all one-dimensional formal group laws over a ring without nilpotents are commutative.
Let $ F ( X ,\ Y ) $
be a one-dimensional formal group law. Define inductively $ [n] (X) = F ( X ,\ [ n - 1 ] (X) ) $ ,
$ n \geq 2 $ ,
$ [1] (X) = X $ .
Let $ F $
be defined over a field $ k $
of characteristic $ p > 0 $ .
Then $ [p] (X) $
is necessarily of the form $ X ^ {p ^{h}} + $ (
higher degree terms) or is equal to zero. The positive integer $ h $
is called the height of $ F $ ;
if $ [p] (X) = 0 $ ,
the height of $ F $
is taken to be $ \infty $ .
Over an algebraically closed field of characteristic $ p > 0 $
the one-dimensional formal group laws are classified by their heights, and all heights $ 1 ,\ 2 \dots \infty $
occur.
Let $ F ( X ,\ Y ) $
be a one-dimensional formal group law over a ring $ A $
in which every prime number except $ p $
is invertible, e.g. $ A $
is the ring of integers of a local field of residue characteristic $ p $
or $ A $
is a field of characteristic $ p $ .
Assume for the moment that $ A $
is of characteristic zero and let$$
f (X) = X + a _{2} X ^{2} + a _{3} X ^{3} + \dots
$$
be the logarithm of $ F ( X ,\ Y ) $ .
Then $ F ( X ,\ Y ) $
is strictly isomorphic over $ A $
to the formal group law $ F _{(p)} ( X ,\ Y ) $
whose logarithm is equal to$$
f _{(p)} (X) = X + a _{p} X ^{p} + a _ {p ^{2}} X ^ {p ^{2}} + \dots .
$$
The result extends to the case that $ A $
is not of characteristic zero and to more-dimensional commutative formal group laws. $ F _{(p)} ( X ,\ Y) $
is called the $ p $ -
typification of $ F ( X ,\ Y ) $ .
References
| [a1] | J.T. Tate, "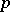 -divisible groups" T.A. Springer (ed.) et al. (ed.) , Proc. Conf. local fields (Driebergen, 1966) , Springer (1967) pp. 158–183 MR0231827 Zbl 0157.27601 -divisible groups" T.A. Springer (ed.) et al. (ed.) , Proc. Conf. local fields (Driebergen, 1966) , Springer (1967) pp. 158–183 MR0231827 Zbl 0157.27601 |
| [a2] | J.-P. Serre, "Groupes 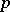 -divisible (d' après J. Tate)" Sem. Bourbaki , 19, Exp. 318 (1966–1967) MR1610452 MR0393040 -divisible (d' après J. Tate)" Sem. Bourbaki , 19, Exp. 318 (1966–1967) MR1610452 MR0393040 |
| [a3] | M. Hazewinkel, "Formal groups and applications" , Acad. Press (1978) MR0506881 MR0463184 Zbl 0454.14020 |
| [a4] | M. Demazure, P. Gabriel, "Groupes algébriques" , 1 , Masson & North-Holland (1970) MR0302656 MR0284446 Zbl 0223.14009 Zbl 0203.23401 |
| [a5] | J. Lubin, J. Tate, "Formal complex multiplication in local fields" Ann. of Math. , 81 (1965) pp. 380–387 MR0172878 Zbl 0128.26501 |
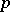 -divisible groups" T.A. Springer (ed.) et al. (ed.) , Proc. Conf. local fields (Driebergen, 1966) , Springer (1967) pp. 158–183 MR0231827 Zbl 0157.27601
-divisible groups" T.A. Springer (ed.) et al. (ed.) , Proc. Conf. local fields (Driebergen, 1966) , Springer (1967) pp. 158–183 MR0231827 Zbl 0157.27601 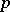 -divisible (d' après J. Tate)" Sem. Bourbaki , 19, Exp. 318 (1966–1967) MR1610452 MR0393040
-divisible (d' après J. Tate)" Sem. Bourbaki , 19, Exp. 318 (1966–1967) MR1610452 MR0393040