Weyl algebra
Let $ K $
be a commutative field and $ n $
a positive integer. The ring of differential operators with coefficients in the polynomial ring $ K [ x ] = K [ x _ {1} \dots x _ {n} ] $
is denoted by $ A _ {n} ( K) $
and called the Weyl algebra in $ n $
variables over $ K $.
Identifying $ K[ x] $
with the subring of zero-order differential operators, it follows that the ring $ A _ {n} ( K) $
is generated by $ K[ x] $
and the derivation operators $ \{ \partial _ {i} = \partial / \partial x _ {i} \} _ {1} ^ {n} $.
The commutators $ [ \partial _ {i} , x _ {i} ] = 1 $
for every $ i $.
So $ A _ {n} ( K) $
is a non-commutative ring. Every element has a unique representation
$$ P( x, \partial ) = \sum _ {v = 0 } ^ { m } p _ \alpha ( x) \partial ^ \alpha , $$
where $ \partial ^ \alpha $ are monomials in the derivation operators. The largest integer $ m $ such that a polynomial coefficient $ p _ \alpha ( x) $ is non-zero with $ | \alpha | = m $ is the order of the differential operator $ P $. The order yields a filtration (cf. Filtered module) and the associated graded ring (cf. Graded module)
$$ \mathop{\rm gr} ( A _ {n} ( K)) = \oplus _ {m \geq 0 } \mathop{\rm gr} _ {m} ( A _ {n} ( K) ), $$
where $ \mathop{\rm gr} _ {m} ( A _ {n} ( K) ) $ is the set of operators of order $ m $, divided by those of order $ m - 1 $ at most. It is well-known that the associated graded ring is isomorphic to the polynomial ring in $ 2n $ variables over $ K $, where $ \{ \sigma _ {0} ( x _ {\mathbf . } ) , \sigma _ {1} ( \partial _ {\mathbf . } ) \} $ are the generators.
Ring-theoretic properties.
Here only the case when the field $ K $ has characteristic zero is discussed. If $ \mathop{\rm char} ( K) > 0 $, the results below are no longer valid. For material when $ \mathop{\rm char} ( K) > 0 $ see [a30]. From now on $ \mathop{\rm char} ( K) = 0 $. Then $ A _ {n} ( K) $ is a simple ring and since $ \mathop{\rm gr} ( A _ {n} ( K)) $ is Noetherian and commutative, it follows that $ A _ {n} ( K) $ is both left and right Noetherian. By [a43], every left ideal of $ A _ {n} ( K) $ is generated by two elements. The global homological dimension of $ A _ {n} ( K) $ is equal to $ n $. This result was proved in [a37]. The case $ n = 1 $ was settled before in [a35]. Another important result is the involutivity of characteristic ideals.
To explain this, one considers a finitely-generated left $ A _ {n} ( K) $- module $ M $. A good filtration on $ M $ consists of an increasing sequence of $ K[ x] $- submodules $ \{ M _ {v} \} $ such that $ \partial _ {i} M _ {v} \subset M _ {v+1} $ for all pairs $ i, v $, and the associated graded module $ \oplus M _ {v} / M _ {v-1} $ is finitely generated over $ \mathop{\rm gr} ( A _ {n} ( K)) $. A module can be equipped with different good filtrations. But there exists a unique graded ideal of $ \mathop{\rm gr} ( A _ {n} ( K)) $, given as the radical of the annihilating ideal of $ \oplus M _ {v} / M _ {v-1} $ for any good filtration. It is denoted by $ J( M) $ and called the characteristic ideal of $ M $. On $ \mathop{\rm gr} ( A _ {n} ( K)) $ there exists a Poisson product such that $ \{ \sigma _ {1} ( \partial _ {v} ) , \sigma _ {0} ( x _ {i} ) \} = \Delta _ {iv} $. The involutivity theorem asserts that
$$ \tag{a1 } \{ J ( M) , J( M) \} \subset J( M) $$
for every finitely-generated left $ A _ {n} ( K) $- module. In the special case when $ K = \mathbf C $, the Nullstellen Satz (cf. Hilbert theorem) identifies $ J( M) $ with an algebraic set in the symplectic cotangent space $ T ^ {*} ( \mathbf C ^ {n} ) $, denoted by $ \mathop{\rm Char} ( M) $ and called the characteristic variety of $ M $( cf. also Characteristic manifold). Then (a1) means that $ \mathop{\rm Char} ( M) $ is involutive in the symplectic cotangent space.
The involutivity implies that the dimension of $ \mathop{\rm gr} ( A _ {n} ( K)) / J( M) $ is at least $ n $ when $ M $ is a non-zero $ A _ {n} ( K) $- module. This can be used to prove that $ \mathop{\rm gl}.dim ( A _ {n} ( K)) = n $, using the fact that $ A _ {n} ( K) $ is a regular Auslander ring. See [a8] for a survey of this. The result (a1) was proved by micro-local analysis in [a40]. An algebraic proof was found later in [a14]. In [a26] characteristic ideals were used to show that if $ W \subset \mathop{\rm gr} ( A _ {n} ( K)) $ is a multiplicative set formed by homogeneous elements and $ S $ is the multiplicative set in $ A _ {n} ( K) $ whose principal symbols belong to $ W $, then $ S $ satisfies the two-sided Ore condition. So the universal $ S $- inverting ring is the two-sided ring of Ore fractions $ S ^ {-1} A _ {n} ( K) $. In particular, this applies when $ S $ is the set of non-zero elements. The resulting division ring $ D _ {n} ( K) $ is related to division rings of certain enveloping algebras divided by primitive ideals.
Holonomic modules.
The equality $ \mathop{\rm gl}.dim ( A _ {n} ( K)) = n $ implies that its Krull dimension is at most $ n $. The equality $ \mathop{\rm Kr}.dim ( A _ {n} ( K)) = n $ was actually proved before the discoveries above in [a15], using a trace formula which shows that every non-zero $ A _ {1} ( K) $- module is an infinite-dimensional vector space over $ K $. Of special interest is the set of finitely-generated left or right $ A _ {n} ( K) $- modules $ M $ such that $ \mathop{\rm dim} ( \mathop{\rm gr} ( K) / J( M)) = n $. Such modules are called holonomic and enjoy finiteness properties, e.g. every holonomic module is Artinian. The converse is not true, since [a43] gives examples of cyclic modules $ M = A _ {n} ( K) / A _ {n} ( K) P $ which are simple. Here $ n $ is any positive integer and $ J ( M) $ is a principal ideal, so $ M $ is non-holonomic when $ n > 1 $.
An important class of holonomic modules arise as follows: If $ P( x) \in K[ x] $, then the subring of rational functions $ K[ x, P ^ {-1} ] $ is a holonomic $ A _ {n} ( K) $- module. This was proved by J. Bernstein in [a3], [a4], in which also a functional equation was found expressed by the equality:
$$ \tag{a2 } b( s) P( x) ^ {s} = \sum s ^ {v} Q _ {v} ( x, \partial ) ( P( x) ^ {s+1} ) . $$
Here $ b( s) $ is a polynomial, chosen to have smallest possible degree and highest coefficient one. It is called the Bernstein–Sato polynomial of $ P $. The case when $ K = \mathbf C $ is of particular interest. It is proved in [a27] that the roots of $ b( s) $ consist of strictly negative rational numbers. See also [a6] for this. The roots of $ b( s) $ are related to the monodromy acting in $ X = \mathbf C ^ {n} \setminus P ^ {-1} ( 0) $ under the mapping $ P : X \rightarrow \mathbf C ^ {*} $, where it is assumed that zero is the only critical value of $ P $. In [a31] it is proved that the union $ \{ {e ^ {- 2 \pi i \alpha } } : {\alpha \in b ^ {-1} ( 0) } \} $ is equal to the union of eigenvalues of monodromy in every dimension in $ \mathbf C ^ {n} \setminus P $. Bernstein's functional equation gives meromorphic continuations of distributions. The meromorphic $ \mathfrak D \mathfrak b ( \mathbf C ^ {n} ) $- valued function $ \mu _ {s} = \int | P | ^ {2s} $ exists, with poles contained in the set $ \{ {\cup ( \alpha - v ) } : {\alpha \in b ^ {-1} ( 0) \textrm{ and } v \in \mathbf N } \} $. The roots of the $ b $- function give an effective contribution to the set of poles. Namely, for any root $ \alpha $ of $ b( s) $ there exists some $ v \in \mathbf N $ such that $ \alpha - v $ is a pole of $ \mu _ {s} $. This is proved in [a1].
Fundamental solutions.
Let $ P( D) $ be a differential operator with constant coefficients. Using the Fourier transform, and replacing $ \mathbf C ^ {n} $ by $ \mathbf R ^ {n} $, the $ \mathfrak D \mathfrak b ( \mathbf R ^ {n} ) $- valued function $ \mu _ {s} $ exists, acting on test-forms $ \phi ( x) $ by
$$ \langle \mu _ {s} , \phi \rangle = \int\limits _ {\mathbf R ^ {n} } P( \xi ) ^ {-1} | P ( \xi ) | ^ {2s} \widehat \phi d \xi . $$
The constant term $ \mu _ {0} $ at $ s = 0 $ gives a fundamental solution to $ P( D) $. Using results about regular holonomic modules it can be proved that the analytic wave front set of $ \mu _ {0} $ is equal to its $ C ^ \infty $ wave front set when the polynomial is homogeneous. For more results about Fourier transforms and $ D $- modules with polynomial coefficients see [a32] (and also $ D $- module).
The Weyl algebra is a special case of rings of differential operators on non-singular algebraic varieties. See [a36] and [a20] for such constructions, which were made before the detailed study of Weyl algebras started.
But foremost $ A _ {n} ( K) $ is fundamental in algebraic $ D $- module theory. The reason is that any quasi-projective manifold $ X $ over $ \mathbf C $ is covered in the Zariski topology by charts given by affine manifolds $ V $ for which there exists an unramified covering mapping onto $ \mathbf C ^ {n} \setminus T $, where $ n = d _ {X} $ and $ T \subset \mathbf C ^ {n} $ is an algebraic hypersurface. The ring of differential operators on the affine algebra $ {\mathcal O} ( V) $ of regular functions on $ V $ is equal to $ {\mathcal O} ( V) \otimes _ {\mathbf C [ x] } A _ {n} ( \mathbf C ) $. For algebraic $ D $- module theory see [a9].
Fuchsian filtrations.
Above, the filtration on $ A _ {n} ( K) $ defined by the usual order of differential operators was considered. The Weyl algebra can be endowed with other filtrations, which no longer are positive. With $ X = \mathbf C ^ {n+1} $ and coordinates $ x _ {1} \dots x _ {n} , t $ one takes the hyperplane $ \{ t = 0 \} $, and the filtration on $ A _ {n+1} ( \mathbf C ) $ is such that $ \mathop{\rm deg} ( t) = - 1 $, $ \mathop{\rm deg} ( \partial / \partial t) = 1 $, while $ x _ {v} $ and $ \partial / \partial x _ {v} $ are of degree zero for every $ v $. The associated graded ring is $ A _ {n+1} ( \mathbf C ) $. The associated Rees ring of the Fuchsian filtered ring is Noetherian and its global homological dimension is $ ( 2n+ 1 ) $. This ring has interest in its own and appears in more extensive classes of rings, [a41]. The Fuchsian filtration is adapted to study nearby and vanishing cycles (cf. Vanishing cycle). If $ M $ is a holonomic $ A _ {n+1} ( \mathbf C ) $- module, then there exists a unique good filtration $ V _ {\mathbf . } ( M) $ with respect to the Fuchsian filtration such that the minimal polynomial of the Euler mapping on $ \oplus V _ {k} ( M)/V _ {k-1} ( M) $ has roots in the lattice $ \{ 0 \leq \mathop{\rm Re} ( \lambda ) < 1 \} $. One refers to this as the Kashiwara–Malgrange filtration. Every homogeneous quotient $ V _ {k} ( M) / V _ {k-1} ( M) $ is a holonomic module over the $ n $- dimensional Weyl algebra in the $ x $- variables. When $ M $ is regular holonomic and the Riemann–Hilbert correspondence is applied, one proves that the de Rham complex of $ V _ {0} ( M)/ V _ {-1} ( M) $ is the nearby cycle along $ \{ t = 0 \} $ of the perverse sheaf complex defined by the de Rham complex of $ M $. For further details see [a16].
One should also mention the Bernstein filtration on the Weyl algebra, where both $ x _ {v} $ and $ \partial _ {v} $ have degree $ + 1 $. For $ n = 1 $, [a44] contains a description of the graded ideals of $ K[ x, y] $ which are generated by principal symbols of elements in a left ideal of $ A _ {1} ( K) $, using the Bernstein filtration to identify $ K[ x, y] $ with $ \mathop{\rm gr} ( A _ {1} ( K)) $.
Weyl algebras with coefficients in a ring exist, i.e. for any ring $ R $ the ring $ A _ {n} ( R) = A _ {n} ( \mathbf Z ) \otimes _ {\mathbf Z } R $ exists. New phenomena may occur when $ R $ is non-commutative. The work [a19] shows that if $ D $ is the skew-field given by the quotient field $ D _ {1} ( K) $, then the ring $ A _ {1} ( D) $ has global dimension $ 2 $. For further results of Weyl algebras over division rings see [a18]. If $ R $ is a commutative Noetherian and regular $ \mathbf Q $- algebra, one has
$$ \mathop{\rm gl}.dim ( A _ {n} ( R)) = n + \mathop{\rm gl}.dim ( R). $$
See [a6] and [a17] for this result and various extensions, where the global homological dimension is computed for other classes of rings of differential operators. If $ S $ is a non-commutative $ \mathbf Q $- algebra equipped with a Zariskian filtration such that $ \mathop{\rm gr} ( S) $ is a commutative regular Noetherian ring, one constructs $ A _ {1} ( S) = A _ {1} ( \mathbf Q ) \otimes _ {\mathbf Q } S $. It is an open problem if $ \mathop{\rm gl}.dim ( A _ {1} ( S))= \mathop{\rm gl}.dim ( S) + 1 $ holds. The work [a13] contains results which predict the grade number of graded modules over $ A _ {1} ( S) $ where the Fuchsian graded structure on $ A _ {1} ( \mathbf Q ) $ induces a graded ring structure on $ A _ {1} ( S) $.
Invariant theory is another topic where the Weyl algebra appears. In [a29] it is proved that if $ G $ is a finite group of automorphisms on $ \mathbf C [ x _ {1} \dots x _ {n} ] $ which does not contain any pseudo-reflection different from the identity, then the ring of differential operators on the $ G $- invariant subring of $ \mathbf C [ x] $ is equal to the $ G $- invariant subring $ \mathop{\rm pf} A _ {n} ( \mathbf C ) $. Moreover, the ring $ A _ {n} ( \mathbf C ) ^ {G} $ is an Auslander–Gorenstein ring whose injective dimension is $ n $. This means that the bimodule given by the ring $ A _ {n} ( \mathbf C ) ^ {G} $ has an injective resolution of length $ n $ both as a left and a right module, and Auslander's condition holds:
$$ \mathop{\rm Ext} _ {A} ^ {v} ( N, \mathop{\rm Ext} _ {A} ^ {k} ( M, A)) $$
$$ \textrm{ for all } v < k \textrm{ and } N \subset \mathop{\rm Ext} _ {A} ^ {k} ( M , A) , $$
where $ A = A _ {N} ( \mathbf C ) ^ {G} $ and $ M $ is any finitely-generated $ A $- module. This condition was originally verified for an extensive class of filtered rings, including the Weyl algebra in [a39]. See [a30] for more facts about rings of differential operators related to invariant theory.
Noetherian operators.
The Weyl algebra is used in commutative algebra to describe primary ideals by equations with respect to its prime radical. Let $ \mathfrak q \subset \mathbf C [ x _ {1} \dots x _ {n} ] $ be a primary ideal and set $ \sqrt \mathfrak q = \mathfrak p $. Then there exists a finite set $ Q _ {1} \dots Q _ {s} $ in $ A _ {n} ( \mathbf C ) $ such that $ Q _ {v} ( \mathfrak q ) \subset \mathfrak p $ for every $ v $. Conversely, let $ P \in \mathbf C [ x] $ be such that $ Q _ {v} ( P) \in \mathfrak p $ for every $ v $. Then $ P \in \mathfrak q $. So $ \mathbf C [ x]/ \mathfrak q $ becomes a submodule of a direct sum of $ \mathbf C [ x]/ \mathfrak p $. This fact is used in the fundamental principle by Ehrenpreis to represent solutions to homogeneous systems of partial differential equations by absolutely convergent integrals over exponential solutions. See [a23], which also includes a construction of Noetherian operators.
Enveloping algebras.
If $ \mathfrak g $ is a Heisenberg algebra, i.e. a nilpotent finite-dimensional Lie algebra with $ 1 $- dimensional centre $ \mathfrak c $ such that $ [ \mathfrak g , \mathfrak g ] = \mathfrak c $, then $ A _ {n} ( K) $ is a quotient ring of the enveloping algebra over $ \mathfrak g $. Hence $ A _ {n} ( K) $- modules yield representations of $ \mathfrak g $, which are infinite dimensional when $ K $ has characteristic zero. See [a11] for this. Quotients by primitive ideals of enveloping algebras of semi-simple Lie algebras lead to more involved results. The Weyl algebra $ A _ {1} ( K) $ appears in the study of $ U( \mathfrak g ) / ( Q- \lambda ) $, where $ \mathfrak g = \mathfrak s \mathfrak l ( 2 , \mathbf C ) $, $ Q $ is the Casimir operator and $ \lambda \in \mathbf C $. This ring is a subring of $ A _ {1} ( \mathbf C ) $. See [a38], [a39]. Several problems concerned with semi-simple elements of [a11] were proposed in [a12]. For affirmative answers in some cases and related problems to Weyl algebras in many variables see [a24]. Finally one should mention the fundamental result in [a2], which is crucial for applications of algebraic $ D $- module theory to representation theory of Lie algebras. See also [a25]. This gives special interest to the Weyl algebra and related rings, such as the ring of differential operators on the projective space $ \mathbf P _ {n} ( \mathbf C ) $, which were determined in . See also [a21] for $ D $-module theory related to representations of Lie algebras.
References
| [a1] | D. Barlet, " Monodromie et pôles du prolongement méromorphe de $\int_X |f|^{2\lambda}$" Bull. Soc. Math. France , 114 (1986) pp. 247–269 Zbl 0652.32010 |
| [a2] | A.A. Beilinson, J. Bernstein, "Localisation des $\mathfrak{g}$-modules" C.R. Acad. Sci. Paris , 292 (1981) pp. 15–18 MR610137 |
| [a3] | I.N. Bernstein, "Modules over a ring of differential operators. Study of the fundamental solutions to equations with constant coefficients" Funct. Anal. Appl. , 5 : 2 (1971) pp. 89–101 Funkts. Anal. i Prilozh. , 5 : 2 (1971) pp. 1–16 MR0290097 |
| [a4] | J. Bernstein, "The analytic continuation of generalized functions with respect to a parameter" Funct. Anal. Appl. , 6 : 4 (1972) pp. 273–285 Funkts. Anal. i Prilozh. , 6 : 4 (1972) pp. 3–25 Zbl 0282.46038 |
| [a5] | F. Bien, "$D$-modules and spherical representations of symmetric spaces" , Princeton Univ. Press (1986) |
| [a6] | J.-E. Björk, "Rings of differential operators" , North-Holland (1979) MR0549189 Zbl 0499.13009 |
| [a7] | J.-E. Björk, "The global homological dimension of some algebras of differential operators" Invent. Math. , 17 (1972) pp. 67–78 MR0453846 MR0320078 Zbl 0255.13010 |
| [a8] | J.-E. Björk, "Non-commutative Noetherian rings and their use in homological algebra" J. Pure Appl. Algebra , 38 (1985) pp. 111–119 |
| [a9] | A. Borel, et al., "Algebraic $D$-modules" , Acad. Press (1987) MR882000 |
| [a10a] | W. Borho, J.-L Brylinski, "Differential operators on homogeneous spaces I" Invent. Math. , 69 (1982) pp. 437–476 MR0679767 Zbl 0504.22015 |
| [a10b] | W. Borho, J.-L Brylinski, "Differential operators on homogeneous spaces II" Invent. Math. , 80 (1985) pp. 1–68 MR1015807 Zbl 0702.22019 |
| [a11] | J. Dixmier, "Algèbres enveloppantes" , Gauthier-Villars (1974) MR0498737 MR0498740 MR0498742 Zbl 0308.17007 |
| [a12] | J. Dixmier, "Sur les algèbres de Weyl II" Bull. Sci. Math. , 94 (1970) pp. 289–301 MR0299632 Zbl 0202.04303 |
| [a13] | E.K. Ekström, "Homological properties of some Weyl algebra extensions" Compositio Math. , 75 (1989) pp. 231–246 MR1065208 Zbl 0717.16032 |
| [a14] | O. Gabber, "The integrability of the characteristic variety" Amer. J. Math. , 103 (1981) pp. 445–468 MR0618321 Zbl 0492.16002 |
| [a15] | P. Gabriel, R. Rentschler, "Sur la dimension des anneaux et ensembles ordonnes" C.R. Acad. Sci. Paris , 265 (1967) pp. A712-A715 MR0224644 Zbl 0155.36201 |
| [a16] | V. Ginsburg, "Characteristic varieties and vanishing cycles" Inv. Math. , 84 (1986) pp. 327–403 MR0833194 Zbl 0598.32013 |
| [a17] | K.R. Goodearl, R.B. Warfield Jr., "Krull dimension of differential operator rings" Proc. London Math. Soc. , 45 (1982) pp. 49–70 MR0662662 Zbl 0493.16004 Zbl 0491.13018 |
| [a18] | K.R. Goodearl, T.J. Hodges, T.H. Lenagan, "Krull and global dimensions of Weyl algebras over division rings" J. Algebra , 91 (1984) pp. 334–359 MR0769578 Zbl 0558.16002 |
| [a19] | R. Hart, "A note on tensor products of algebras" J. Algebra , 21 (1972) pp. 422–427 |
| [a20] | G. Hochschild, B. Kostant, B. Rosenber, "Differential forms on regular affine algebras" Trans. Amer. Math. Soc. , 102 (1962) pp. 383–408 MR0142598 Zbl 0102.27701 |
| [a21] | R. Hotta, M. Kashiwara, "The invariant system on a semi-simple Lie algebra" Inv. Math. , 75 (1984) pp. 327–358 |
| [a22] | L.V. Hörmander, "The analysis of linear partial differential operators" , 1 , Springer (1983) MR0717035 MR0705278 Zbl 0521.35002 Zbl 0521.35001 |
| [a23] | L. Hörmander, "An introduction to complex analysis in several variables" , North-Holland (1990) MR1045639 Zbl 0685.32001 |
| [a24] | A. Joseph, "The Weyl algebra - semisimple and nilpotent elements" Amer. J. Math. , 97 (1975) pp. 597–615 MR0379615 Zbl 0316.16036 |
| [a25] | A. Joseph, "Primitive ideals in enveloping algebras" , Proc. Internat. Congress Mathematicians (Warszawa, 1983) , 1 , PWN & North-Holland (1984) pp. 403–414 MR0804696 Zbl 0574.17007 |
| [a26] | M. Kashiwara, "A study of over-determined systems" , Kyoto University (1970) (Thesis) |
| [a27] | M. Kashiwara, "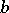 -functions and holonomic systems" Inv. Math. , 38 (1975) pp. 121–135 MR0430304 Zbl 0354.35082 -functions and holonomic systems" Inv. Math. , 38 (1975) pp. 121–135 MR0430304 Zbl 0354.35082 |
| [a28] | M. Kashiwara, "Regular holonomic 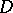 -modules and distributions on complex manifolds" T. Suwa (ed.) P. Wagreich (ed.) , Complex analytic singularities , Adv. Studies in Math. , 8 , Kinokuniya & North-Holland (1987) pp. 199–206 MR894293 -modules and distributions on complex manifolds" T. Suwa (ed.) P. Wagreich (ed.) , Complex analytic singularities , Adv. Studies in Math. , 8 , Kinokuniya & North-Holland (1987) pp. 199–206 MR894293 |
| [a29] | T. Levasseur, "Anneaux d'operateurs differentiels" M.P. Malliavin (ed.) , Sem. P. Dubreil et M.P. Malliavin , Lect. notes in math. , 867 , Springer (157–173) MR0910403 MR0755924 MR0633520 |
| [a30] | T. Levasseur, J.T. Stafford, "Rings of differential operators on classical rings of invariants" Memoirs Amer. Math. Soc. , 41 (1989) MR0988083 Zbl 0691.16019 |
| [a31] | B. Malgrange, "Polynome de Bernstein–Sato et cohomologie evanescente" Asterisque , 101–102 (1983) pp. 243–267 MR0737934 |
| [a32] | B. Malgrange, "Equations différentiels à coefficients polynomiaux" , Birkhäuser (1991) MR1117227 |
| [a33] | J.C. McConnel, "Noncommutative Noetherian rings" , Wiley (1987) |
| [a34] | P. Revoy, "Algèbres de Weyl en caracteristique 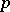 " C.R. Acad. Sci. Paris , 276 (1973) pp. 225–228 MR0335564 Zbl 0265.16007 " C.R. Acad. Sci. Paris , 276 (1973) pp. 225–228 MR0335564 Zbl 0265.16007 |
| [a35] | G.S. Rinehart, "Note on the global dimension of a certain ring" Proc. Amer. Math. Soc. , 13 (1963) pp. 195–222 MR0137747 |
| [a36] | G.S. Rinehart, "Differential forms on general commutative algebras" Trans. Amer. Math. Soc. , 103 (1963) pp. 195–222 MR0154906 Zbl 0113.26204 |
| [a37] | J.-E. Roos, "Determination de la dimension homologique globale des algèbres de Weyl" C.R. Acad. Sci. Paris , 274 (1972) pp. A23-A26 MR0292914 Zbl 0227.16021 |
| [a38] | J.-E. Roos, "Properties homologiques des quotients primitifs des algèbres enveloppantes des algèbres de Lie semi-simples" C.R. Acad. Sci. Paris , 276 (1973) pp. 351–354 |
| [a39] | J.-E. Roos, "Complements" C.R. Acad. Sci. Paris , 276 (1973) pp. 447–450 MR0318250 Zbl 0261.17011 |
| [a40] | M. Kashiwara, "Microfunctions and pseudo-differential equations" H. Komatsu (ed.) , Hyperfunctions and pseudodifferential equations. Proc. Conf. Katata, 1971 , Lect. notes in math. , 287 , Springer (1973) pp. 265–529 MR0420735 Zbl 0277.46039 |
| [a41] | S.P. Smith, "Differential operators in commutative algebras" , Lect. notes in math. , 1197 , Springer (1986) pp. 165–177 |
| [a42] | J.T. Stafford, "Non-holonomic modules over Weyl algebras and enveloping algebras" Inv. Math. , 79 (1985) pp. 619–638 MR782240 Zbl 0558.17011 |
| [a43] | J.T. Stafford, "Module structure of Weyl algebras", London Math. Soc., Ser. II, 18 (1978), pp. 429–442 MR0518227 |
| [a44] | P. Strömbeck, "On left ideals in 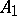 and their associated graded ideals" J. Algebra , 55 (1978) pp. 116–144 MR0515764 Zbl 0399.16002 and their associated graded ideals" J. Algebra , 55 (1978) pp. 116–144 MR0515764 Zbl 0399.16002 |
| [a45] | J.-E. Björk, "Analytic 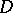 -modules" , Kluwer (1993) MR1232191 -modules" , Kluwer (1993) MR1232191 |
Weyl algebra. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Weyl_algebra&oldid=55213