Variation of a univalent function
A concept in the theory of univalent functions (cf. Univalent function). In a given domain $ D $
of the complex plane let there be given a function $ f( z) $
and a family $ F( z, \lambda ) $
of functions depending on a real parameter $ \lambda $,
$ 0 \leq \lambda \leq \Lambda $,
$ \Lambda > 0 $,
which are univalent in $ D $
for all $ \lambda \in [ 0, \Lambda ] $.
Suppose that $ F( z, 0) = f( z) $.
One forms the difference $ F( z, \lambda ) - f( z) \equiv \Phi ( z, \lambda ) $.
The $ n $-
th order variation, or the $ n $-
th variation, $ n = 1, 2 \dots $
of the function $ f( z) $(
along the family $ F( z, \lambda ) $)
is the coefficient $ {q _ {n} } ( z) $
of $ \lambda ^ {n} $
in the expansion of $ \Phi ( z, \lambda ) $
with respect to the parameter $ \lambda $,
on the condition that the residual term
$$ \phi _ {n} ( z , \lambda ) = \ \Phi ( z , \lambda ) - q _ {1} ( z) \lambda - \dots - q _ {n} ( z) \lambda ^ {n} $$
has a higher order of smallness than $ \lambda ^ {n} $, uniformly with respect to $ z $ in $ D $, on compact sets in $ D $ or in the closure of $ D $. The selection of one of these additional conditions is usually determined by the nature of the problem whose solution involves variational methods connected with the variation of a univalent function.
J. Hadamard [1] and M.A. Lavrent'ev [2] were the first to compute and to give applications of first-order variations. To obtain variations in some specific class of univalent functions often is a complicated task by itself, on account of the non-linear nature of families of such functions. This task was solved for certain classes of functions in simply-connected and multiply-connected domains.
References
| [1] | J. Hadamard, "Leçons sur le calcul des variations" , 1 , Hermann (1910) |
| [2] | M.A. Lavrent'ev, "On some properties of univalent functions" Mat. Sb. , 4(46) : 3 (1938) pp. 391–458 (In Russian) (French abstract) |
| [3] | G.M. Goluzin, "Geometric theory of functions of a complex variable" , Transl. Math. Monogr. , 26 , Amer. Math. Soc. (1969) (Translated from Russian) |
| [4] | K.I. Babenko, "The theory of extremal problems for univalent functions of class 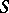 " Proc. Steklov Inst. Math. , 101 (1975) Trudy Mat. Inst. Steklov. , 101 (1972) " Proc. Steklov Inst. Math. , 101 (1975) Trudy Mat. Inst. Steklov. , 101 (1972) |
Comments
The dominant figure in the theory of variations of univalent functions in the first half of the 20th century has been M.M. Schiffer, whose earliest work in this area predates even that of Lavrent'ev. See the bibliography in [a2] for references to Schiffer's work. The most complete treatment of the subject currently available can be found in [a1]; see also the discussion in [a2].
See also Internal variations, method of; Boundary variation, method of.
References
| [a1] | J.A. Hummel, "Lectures on variational methods in the theory of univalent functions" , Univ. Maryland (1972) |
| [a2] | P.L. Duren, "Univalent functions" , Springer (1983) pp. Sect. 10.11 |
Variation of a univalent function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Variation_of_a_univalent_function&oldid=49117