Internal variations, method of
A method in the theory of functions of a complex variable which is employed in solving extremal problems in classes of univalent and multivalent analytic functions. The advantages of the method of internal variations consist in the fact that in choosing the variational formulas on which it is based no assumptions are made on the behaviour of the functions being varied on the boundary of their domain of definition 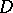 , while the variational formulas themselves are a consequence of variations (modifications) of the functions in the class in a "uniform manner" on interior subsets of
, while the variational formulas themselves are a consequence of variations (modifications) of the functions in the class in a "uniform manner" on interior subsets of 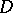 . The method of internal variations was proposed by M. Schiffer [1] for univalent functions in the disc
. The method of internal variations was proposed by M. Schiffer [1] for univalent functions in the disc 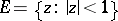 , and was further developed by G.M. Goluzin [2]. They established the following variational formula, which is applicable to the class
, and was further developed by G.M. Goluzin [2]. They established the following variational formula, which is applicable to the class 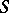 of functions
of functions 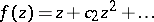 that are holomorphic and univalent in
that are holomorphic and univalent in 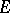 :
:
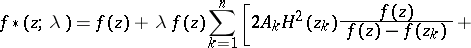 |
 |
where
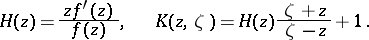 |
Here, 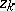 (
(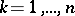 ;
; 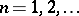 ) are fixed points in
) are fixed points in 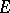 ,
, 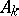 are arbitrary complex constants, while
are arbitrary complex constants, while 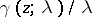 , as
, as 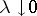 , uniformly tends to zero with respect to
, uniformly tends to zero with respect to  on compact sets inside
on compact sets inside 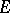 . In other words, in the class
. In other words, in the class 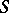 , which is not a linear space, for all functions
, which is not a linear space, for all functions 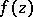 there can be specified a one-parameter family
there can be specified a one-parameter family  ,
, 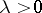 , of functions of the same class such that on any closed set in
, of functions of the same class such that on any closed set in 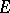 the expansion of
the expansion of 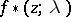 in powers of
in powers of 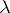 is given by the above formula. Similar formulas (with an estimate of the order of smallness of the residual term on compact sets inside the respective domain) are also valid for other classes of analytic functions.
is given by the above formula. Similar formulas (with an estimate of the order of smallness of the residual term on compact sets inside the respective domain) are also valid for other classes of analytic functions.
A characteristic feature of the method of internal variations is that differential equations for boundary or extremal functions may be obtained from the variational formulas. The study of such equations, involving the use of the analytical theory of differential equations, yields important qualitative results, and in a number of cases a complete solution of the extremal problem may be obtained.
The method has been successfully employed in problems on non-overlapping domains, and has become a constituent part of the so-called variation-parametric method [3].
References
| [1] | M. Schiffer, "Variation of the Green function and the theory of 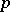 -valued functions" Amer. J. Math. , 65 : 2 (1943) pp. 341–360 -valued functions" Amer. J. Math. , 65 : 2 (1943) pp. 341–360 |
| [2] | G.M. Goluzin, "Variational methods in conformal mappings I" Mat. Sb. , 19 (61) : 2 (1946) pp. 203–236 (In Russian) (English abstract) |
| [3] | G.M. Goluzin, "Geometric theory of functions of a complex variable" , Transl. Math. Monogr. , 26 , Amer. Math. Soc. (1969) (Translated from Russian) |
Comments
The method developed by Schiffer is also called (the method of) interior variation, while its generalization by Goluzin is also called (the method of) Goluzin variation, cf. [a1] for more details and references.
References
| [a1] | P.L. Duren, "Univalent functions" , Springer (1983) pp. Sect. 10.11 |
Internal variations, method of. I.A. Aleksandrov (originator), Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Internal_variations,_method_of&oldid=18190