Tests
in cybernetics
One of the most important means of logical analysis of information. Tests were first used in the problems of controlling the functioning of an electrical circuit. Later pattern recognition algorithms were developed on the basis of tests. The test approach can be applied successfully in many areas of mathematics. The fundamental problems concerning tests can be formulated in the following way.
1) One is given a rectangular table consisting of $ s $ rows and $ m $ columns. The rows are characterized by questions (marks) $ e _ {1} \dots e _ {s} $ from some set $ E $, and the columns by objects (patterns) $ f _ {1} \dots f _ {m} $ from some set $ F $.
<tbody> </tbody>
|
The entry in the cell at the intersection of the $ i $- th row and the $ j $- th column is an answer $ f _ {j} ( e _ {i} ) $( the value of the $ i $- th mark for the $ j $- th pattern), which lies in some set $ G $. Thus, as long as $ e _ {i _ {1} } \neq e _ {i _ {2} } $ for $ i _ {1} \neq i _ {2} $ one can consider the $ j $- th column $ ( 1 \leq j \leq m) $ as a function $ f _ {j} ( x) $. It is natural to regard the columns as being pairwise distinct. Since the nature of the sets $ E $ and $ G $, respectively, is irrelevant, from now on $ E = \{ 0 \dots s - 1 \} $ and $ G = \{ 0 \dots k - 1 \} $. In certain cases there is a partial order $ \leq $ given on $ E $ and $ G $. Sometimes the columns are written as probabilities $ p _ {1} \dots p _ {m} $( $ \sum _ {i} p _ {i} = 1 $).
2) One defines the aim of the logical analysis of the table. For this one fixes some subset $ \mathfrak N $ of pairs $ ( i, j) $, $ i \neq j $, of column numbers. In particular, if the set $ F $ is partitioned into classes, $ ( i, j) \in \mathfrak N $ if and only if $ f _ {i} $ and $ f _ {j} $ belong to the same class and $ i \neq j $. The subset $ \mathfrak N $ can be interpreted as a relation, or as some property.
There are two special cases: 1) $ \mathfrak N = \{ {( 1, j) } : {j = 2 \dots m } \} $ and $ f _ {1} $ is a distinguishing function (this case is connected with the verification problem); 2) $ \mathfrak N = \{ {( i, j) } : {i, j = 1 \dots m, i \neq j } \} $, related to the diagnostic problem (complete recognition).
The aim of the logical analysis can be formulated as follows: To obtain a procedure that, for any $ i, j $ such that $ ( i, j) \in \mathfrak N $, will distinguish the pattern $ f _ {i} $ from the pattern $ f _ {j} $. If $ \mathfrak N $ corresponds to a partition of $ F $ into classes, then the problem is equivalent to that of placing any given function $ f $ from $ F $ into the appropriate class. Below, mainly this problem will be discussed. The question as formulated has a trivial solution, given complete knowledge of the table and of the function $ f $. In actual problems it is possible to obtain information about $ f $, but at a certain cost. Moreover, for a large class of problems the complete table is either unknown, or so large that one cannot work with it. Hence one is restricted to a certain part of it — a so-called representative sample, and the problem appears in a heuristic form.
3) There turns out to be an admissible way for solving the problem. Suppose some function $ f $ in $ F $ is unknown. One needs a way of asking questions, by naming certain rows $ e _ {i _ {1} } \dots e _ {i _ {r} } $, whose answers $ f ( e _ {i _ {1} } ) \dots f ( e _ {i _ {r} } ) $ determine to which class $ f $ belongs. The given interrogation can take place either by means of a so-called absolute experiment (cf. Automata, experiments with), where the questions $ e _ {i _ {1} } \dots e _ {i _ {r} } $ are all asked simultaneously and the answers $ f ( e _ {i _ {1} } ) \dots f ( e _ {i _ {r} } ) $ are analyzed, or by means of a more general process, a so-called conditional experiment, where the questions are asked in turn, and each next question is asked dependent on the previous questions and answers (and taking into account the partial order $ \leq $, if present). A conditional experiment can be represented in the form of an oriented tree, where the vertices represent the questions, the edges represent the answers and the branches represent the outcomes of the experiment. For the following table, three experiments $ E _ {1} $, $ E _ {2} $, $ E _ {3} $ are presented in Fig. a.
<tbody> </tbody>
|
$ E _ {1} E _ {2} E _ {3} $
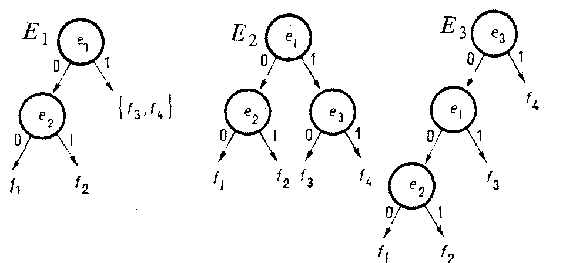
Figure: t092470a
A system $ T $ of questions and the information necessary for it (answers), enabling one to distinguish the property $ \mathfrak N $, is called a test of the initial table.
In the case of an absolute experiment, it is usually understood that a test is a collection $ \{ e _ {i _ {1} } \dots e _ {i _ {r} } \} $ of questions such that for any $ ( i, j) \in \mathfrak N $ there exists an $ e \in T $ with $ f _ {i} ( e) \neq f _ {j} ( e) $( the condition for recognizing $ \mathfrak N $). For many-valued (and not-everywhere defined) tables one can replace the predicate $ \neq $ by other predicates.
In the case of a conditional experiment, a test $ T $ is an oriented tree obtained from a conditional experiment $ E $ by removing all the final edges, and enabling one to recognize the property $ \mathfrak N $. Thus, in the examples given above for the diagnostic problem, $ \{ e _ {1} , e _ {2} , e _ {3} \} $ will be an absolute test; the experiments $ E _ {2} $ and $ E _ {3} $ yield conditional tests $ T _ {2} $ and $ T _ {3} $, but the experiment $ E _ {1} $ does not lead to a conditional test.
For any $ \mathfrak N $ the set $ T _ {0} = \{ e _ {1} \dots e _ {s} \} $ is an absolute test (the trivial test). If a table has large dimensions, then the trivial test leads to a very laborious process of logical analysis. Hence the question arises of constructing simpler tests. For this one defines the notion of complexity $ l ( T) $ of a test $ T $. Below some variants of the definition of complexity of an absolute test are given:
$ l _ {1} ( T) = r $, here $ l _ {1} ( T) $ denotes the "multiplicity" of a test, that is, the number of elements in the test;
$$ l _ {2} ( T) = \sum _ {j = 1 } ^ { r } l ( e _ {i _ {j} } ), $$
this measure reflects the "time" taken to test a sequential "sample" of elements if $ l ( e _ {i _ {j} } ) $ is interpreted as the realization time for $ e _ {i _ {j} } $;
$$ l _ {3} ( T) = \max l ( e _ {i _ {j} } ), $$
here $ l _ {3} ( T) $ denotes the test time for a parallel "sample" of elements.
Similar complexity characteristics can also be introduced for conditional tests, starting from the corresponding tree, and expressing the number of vertices of the tree, the total length of the tree (the number of edges of the tree) and the maximal length of a branch. If the columns in the table occur with probabilities $ p _ {1} \dots p _ {m} $, then it is natural to take as a measure of complexity the quantity $ \sum _ {i = 1 } ^ {m} l _ {i} p _ {i} $, where $ l _ {i} $ is the length of the branch of the tree leading to $ f _ {i} $. A test for a given table, with control target $ \mathfrak N $ and the above methods of control and measures of complexity, is called minimal if it has minimal complexity. The construction of minimal tests is a central problem of testing theory. The reasons for this can be demonstrated by the example of an absolute test (where the sets $ E $ and $ G $ are not partially ordered). For each table there exists a test $ T $ for which $ l _ {1} ( T) \leq \min ( s, m - 1) $, and one can describe tables for which this bound is best possible. At the same time, for $ m = m ( s) $ and $ s \rightarrow \infty $, for almost-all tables
$$ \mathop{\rm log} _ {2} m \leq \ l _ {1} ( T _ \min ) \leq \ 2 \mathop{\rm log} _ {2} m, $$
in other words, the minimal test $ T _ \min $ is simpler than that described above for a wide range of values of the parameters.
There is an abundance of algorithms for the construction of minimal tests. For example, for absolute tests by examination of the subsets of the set $ \{ e _ {1} \dots e _ {s} \} $, and for conditional tests by examination of trees with bounded branches and bounded number of vertices. These algorithms, however, are extremely laborious. It turns out that the construction of minimal tests is connected with the construction of so-called extremal tests. The notion of extremality allows one to select from the set of all tests those which in a certain sense have no redundancy. An absolute test (without $ \leq $) $ T $ with respect to $ \mathfrak N $ for the initial table is called extremal if none of its proper subsets $ T ^ \prime \subseteq T $ is a test for $ \mathfrak N $. The notion of extremality can be expressed in terms of partitions of the set $ \{ f _ {1} \dots f _ {m} \} $. Let $ R _ {T} $ be the partition of the columns of the table in which two columns belong to the same class if and only if they agree on questions in $ T $. The test $ T $ is extremal if and only if, for any two subsets $ T ^ \prime $ and $ T ^ {\prime\prime} $ of $ T $ such that $ T ^ {\prime\prime} \subseteq T ^ \prime $ and $ T ^ {\prime\prime} \neq T ^ \prime $, there exists a pair $ ( i, j) \in \mathfrak N $ for which $ f _ {i} \equiv f _ {j} $ on $ T ^ {\prime\prime} $ but not on $ T ^ \prime $. That is, if and only if the partition $ R _ {T ^ \prime } $ is a subpartition of the partition $ R _ {T ^ {\prime\prime} } $ with respect to $ \mathfrak N $. For an extremal test $ T $ one has $ l _ {1} ( T) \leq m - 1 $. On the other hand, by discarding elements from any test $ T $ one can obtain an extremal test.
For conditional tests (without $ \leq $), extremality means that every subsequent element $ e $ is chosen such that, for at least one pair $ ( i, j) \in \mathfrak N $, $ f _ {i} $ and $ f _ {j} $ belong to the same component of the partition at the previous stage, but $ f _ {i} ( e) \neq f _ {j} ( e) $, that is, $ f _ {i} $ and $ f _ {j} $ now belong to distinct components of the partition.
In the example, the test $ T = \{ e _ {1} , e _ {2} , e _ {3} \} $ is an absolute extremal test, and $ T _ {2} $ and $ T _ {3} $ are conditional extremal tests. The test $ T _ {2} $ yields a certain "economy" of time in comparison to the absolute test $ T $, in as much as it requires only two elements in each diagnostic situation, as opposed to three for $ T $. Generalizing this example, it is easy to construct tables for which the minimal absolute test has length $ m - 1 $, but the maximal length of a branch in a conditional test is equal to $ \mathop{\rm log} _ {2} m $. This is the greatest advantage that conditional tests have over absolute tests.
In the case where the sets $ E $ and $ G $ are equipped with partial orders $ \leq $, the definition of extremality becomes more complicated. Such a definition exists for tables of automata functions $ \{ f _ {1} \dots f _ {m} \} $, connected with the diagnostics of automata (cf. also Automata, experiments with). Here the elements of $ E $ and $ G $ are words over alphabets $ A $ and $ B $, and the relation $ x \leq y $ means that the word $ x $ is an initial segment of the word $ y $. When a word $ e = a _ {1} \dots a _ {t} $ is fed into the automaton, then so also are entered all the words $ e ^ \prime = a _ {1} \dots a _ {t ^ \prime } $, where $ t ^ \prime \leq t $( all the initial segments of $ e $). Hence redundancy can arise from this element $ e $. More precisely, an element $ e = a _ {1} \dots a _ {t} $ is called irreducible if, for any $ v = 1 \dots t - 2 $, either the transition from the word $ a _ {1} \dots a _ {v} $ to the word $ a _ {1} \dots a _ {v + 1 } $ involves one of the pairs $ ( i, j) \in \mathfrak N $ which belongs to one of the components of the partition $ R ( a _ {1} {} \dots a _ {v} ) $, or one can carry out a special move toward such a partition by way of transition to a new state system $ ( f _ {1} \dots f _ {m} ) $; and for $ v = t - 1 $ the transition definitely involves the partition. It turns out that every word can be made irreducible by discarding particular segments, in such a way that the partition involved is the same as for the original word. The notion of an absolute extremal test is now extended by adding the condition that all the elements of $ T $ be irreducible. The notion of a conditional extremal test has two extra conditions: 1) if the element $ e _ {v} $ is chosen at some stage, then the element $ e _ {v + 1 } $ chosen at the following step must follow $ e _ {v} $: $ e _ {v} \leq e _ {v + 1 } $; and 2) the elements corresponding to extremal vertices of the tree of $ T $ must be irreducible.
The following problems arise in the theory of tests: the construction of effective algorithms for finding various types of tests; the estimation of the number of extremal tests; the classification of tests and tables; and the investigation of the influence of further information about the structure of a table on the complexity of tests and the effectiveness of their construction.
A whole series of diagnostic problems reduces to tabular form.
1) Fault finding in electrical circuits (cf. Reliability and inspection of control systems). Here a circuit $ \Sigma $ which realizes a Boolean function $ f ( x _ {1} \dots x _ {n} ) $ is being tested. The set $ E $ consists of all collections $ ( \alpha _ {1} \dots \alpha _ {n} ) $, $ s = 2 ^ {n} $, $ G = \{ 0, 1 \} $, and $ F $ consists of the Boolean functions $ \{ f _ {1} \dots f _ {m} \} $ which characterize the correct and incorrect states of the circuit.
2) Control of automata. Here the table usually has infinitely-many rows (the set of input words is infinite). However, for the control one needs only those words which are initial segments of irreducible words, and the length of such words is bounded by a constant depending on $ m $ and on the number of states for $ f _ {1} \dots f _ {m} $. The resulting table is finite.
3) Diagnostic problems in medicine. To obtain diagnoses of certain classes of diseases, one sets up a table with rows corresponding to symptoms, and with columns corresponding to the characteristic collection of significant signs for each disease in the class. If the signs are displayed in discrete form (for example, whether temperature is normal, whether blood pressure is normal, etc.), then one obtains a table of the type described above, whereby if the set of signs is sufficiently large, then the columns are pairwise distinct.
4) Recognition of geometric shapes. Suppose that the squares of a discrete table may contain two symbols: 0 or 1. Each of them can have a specific realization, and they are distinguished from one another by their dimensions and positions (Fig. b). One needs to ask questions about the state of a cell in the table (is it shaded or not?) to find out which symbol to write in it. Here $ e _ {1} \dots e _ {s} $ are the numbers of the cells, $ G = \{ 0, 1 \} $, and $ f _ {1} \dots f _ {m} $ are all 0 or 1. The value $ f _ {i} ( e) $ is 1 if the square $ e $ is shaded for $ f _ {i} $, and 0 otherwise.
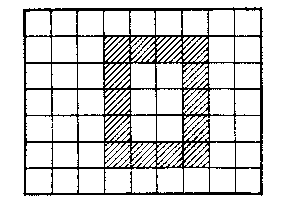
Figure: t092470b
5) Game-theoretic problems. The famous game "battleships" actually consists of recognizing the arrangement of the opponent's "ships" by successive choices of squares, whereby the partner announces the result of each such choice. Here one can build a table with columns characterizing the variants of arranging the "ships" (it is constructed of 0's and 1's, as in the recognition problem). A conditional test would be a way of solving the problem.
6) Minimization of Boolean functions. This reduces to the special test problem in which the table describes the covering of the set $ N _ {f} $( the points at which $ f = 1 $) by so-called maximal faces (corresponding to simple implications of $ f $).
Many classical combinatorial problems can be thought of as test problems, for example, the travelling-salesman problem, the knapsack problem, and also several problems about finding extrema.
Tests allow one to analyze logical connections between marks, and to introduce measures of the importance of marks. For example, one may say that the importance of a mark is defined to be the ratio of the number of all extremal tests. The establishment of measures of importance of marks is useful in the solution of applied problems for the construction of heuristic algorithms. This approach is used successfully in solving diagnostic problems in geology, economics, medicine, etc.
References
| [1] | S.V. Yablonskii, I.A. Chegis, "On tests for electric circuits" Uspekhi Mat. Nauk , 10 : 4 (1955) pp. 182–184 (In Russian) |
| [2] | N.A. Solov'ev, "Tests" , Novosibirsk (1978) (In Russian) |
| [3] | A.N. Dmitriev, Yu.I. Zhuravlev, F.P. Krendelev, "On mathematical principles of classification of objects and events" Diskretn. Anal. , 7 (1966) pp. 3–15 (In Russian) |
Comments
References
| [a1] | B.G. Batchelor, "Pattern recognition" , Plenum (1978) |
| [a2] | K.L. Clark, D.F. Cowell, "Programs, machines, and computation" , McGraw-Hill (1976) |
| [a3] | O. Duda, P.E. Hart, "Pattern classification and scene analysis" , Wiley (1973) |
| [a4] | R.J. Nelson, "Introduction to automata" , Wiley (1968) |
| [a5] | B.A. Trakhtenbrot, Ya.M. Bardzdin', "Finite automata. Behaviour and synthesis" , North-Holland (1973) |
| [a6] | K. Weihrauch, "Computability" , Springer (1987) |
Tests. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Tests&oldid=48958