Classical combinatorial problems
Problems on the selections and arrangements of elements of a finite set, often having as their origin some formulation of light-harted content of brain-teaser type.
One of the classical combinatorial problems featuring in the myths of ancient Orient is the construction of a magic square, that is, an arrangement of the first $ n ^ {2} $ positive integers in an $ n \times n $ square such that the sums of all the rows, columns and diagonals are equal. For example
$$ \begin{array}{ccc} 4 & 9 & 2 \\ 3 & 5 & 7 \\ 8 & 1 & 6 \\ \end{array} $$
is a magic square for $ n = 3 $. A number of methods for constructing such squares are known (see, for example, [1]). The determination of the number of magic squares of order $ n $ for $ n > 4 $ represents a difficult problem which is still unsolved (1978).
A number of combinatorial problems was investigated by L. Euler. One of them, the problem of the 36 officers, which is to arrange this number of officers of 6 different ranks and 6 different regiments in the cells of a $ 6 \times 6 $ square (a squadron) so that each column and each row contains exactly one officer of each rank and exactly one of each regiment. An $ n \times n $ square whose cells contain the elements $ 1 \dots n $ is called a Latin square if the elements of each row and of each column are distinct. Two Latin squares are said to be orthogonal if, on superimposing them, all the $ n ^ {2} $ pairs of elements in the cells are distinct. The problem of the 36 officers is equivalent to that of the existence of a pair of orthogonal Latin squares of order 6. Euler conjectured that there are no orthogonal Latin squares of order $ n = 4 k + 2 $, $ k = 1 , 2 ,\dots $. In 1900, G. Tarry verified this conjecture for $ n = 6 $ and hence proved that the problem of the 36 officers has no solution. In 1959–1960, it was proved that there exists a pair of orthogonal Latin squares for each $ n = 4 k + 2 $, $ k = 2 , 3 ,\dots $( see [2]).
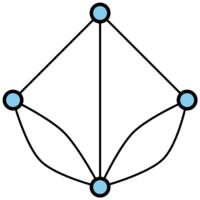
Another problem considered by Euler is the problem of the Königsberg bridges, stated as follows. There are seven bridges joining the banks of a river that runs through a city and two islands situated on the river. It is then asked whether it is possible to go round all the bridges crossing each one just once and return to the starting point. By supposing that vertices correspond to the areas of land and edges to bridges, this problem can be restated in the form of the question whether it is possible to perform a tour on the graph depicted in Fig. a under the condition that each of its edges is used exactly once and that one returns to the starting point (see Graph circuit).
If such a tour is possible on a graph, the graph is said to have an Eulerian cycle. Euler established that such a cycle in a graph exists if and only if the graph is connected and if the number of edges incident to each vertex is even. Since the graph of Fig. a does not satisfy the requirement, the problem of the Königsberg bridges has as solution that the tour is impossible. There is still no tour if one drops the requirement that the starting and finishing points of the tour should be the same. In this case one is solving the problem of the existence of an Eulerian chain in the graph. A graph has an Eulerian chain if and only if it is connected and if the number of vertices incident to an odd number of edges is either 0 or 2. The graph in Fig. a fails to satisfy this condition (see [3]).
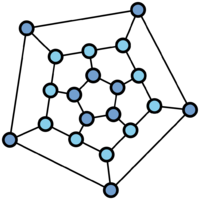
In 1859, W. Hamilton invented a "round-the-world voyage" game. It consists in finding a path passing through all the vertices (cities) of the graph illustrated in Fig. b such that each vertex is visited once and such that one returns to the starting point.
Paths in graphs that posses this property are called Hamiltonian cycles or Hamiltonian circuits. Necessary and sufficient conditions for the existence of a Hamiltonian cycle in a graph are at present (1978) unknown (see [3]).
The problem concerning Hamiltonian cycles in a graph has been given various generalizations. One of these is the travelling salesman problem, which has a number of applications in operations research, in particular in the solution of certain transport problems. It consists of the following: there is a collection of towns, the distances between which are known; it is required to find the shortest path passing through all the towns onces and returning to the origin.
In 1847 T.P. Kirkman posed and solved the problem of the 15 schoolgirls. They had to walk daily in five groups of three. Furthermore, it was required to draw up a schedule for their walks so that each schoolgirl would in the course of seven days finds herself exactly once in the same group as each of the others. This problem is related to that posed by J. Steiner (1853) of constructing a system of triples. A Steiner triple system of order $ v $, denoted by $ \mathop{\rm STS} ( v) $, is a collection of triples from a set of $ v $ elements such that each pair of elements is contained in precisely one triple. The Steiner triple systems have been classified for $ v \leq 15 $. It turns out that for $ v = 3 , 7 , 9 $, the triple systems are unique up to equivalence (permutation of the $ v $ elements, permutation of the triples); for $ v = 13 $ there are two non-equivalent triple systems; for $ v = 15 $ there are 80. For $ v > 15 $ the number of distinct Steiner triple systems is still unknown (1978). For $ v > 3 $ a Steiner triple system is a special case of an incomplete partially-balanced block design.
The classical matching problem consists of the following. There are two identical packs of $ n $ cards. It is required to determine $ D _ {nr} $, $ r = 0 \dots n $, the number of arrangements of the cards in the second pack such that when corresponding cards of each pack are compared the number of matchings is equal to $ r $, $ r = 0 \dots n $. The special case of this problem for $ r = 0 $, known as the derangement problem, was first stated by P. Montmort (1708). Euler considered the problem of finding the number of terms of a determinant having no elements of the principal diagonal; this is equivalent to the determination of $ D _ {n0} $.
The matching problem gave rise to the beginning of the branch of combinatorial analysis related to the study of permutations with restricted positions. A distance $ \rho $ can be introduced on the set $ S _ {n} $ of permutations of degree $ n $ acting on a set $ X $ by setting
$$ \rho ( s , s ^ \prime ) = \ | \{ {x } : {s ( x) \neq s ^ \prime ( x) , x \in X } \} | ,\ \ s , s ^ \prime \in S _ {n} . $$
Then
$$ D _ {nr} = | \{ {s } : { \rho ( s , s ^ \prime ) = n - r , s \in S _ {n} } \} | , $$
and hence
$$ D _ {nr} = \frac{n!}{r!} \sum _ { k= 0 }^ { n- r} ( - 1 ) ^ {k} \frac{1}{k!}\,r = 0 \dots n . $$
In terms of distances between permutations one can formulate yet another classical combinatorial problem, usually called the married couples problem, or problème des ménages. It consists of determining the number $ M _ {n} $ of seatings of $ n $ couples in $ 2 n $ places round a circular table so that no husband sits next to his wife. Then
$$ M _ {n} = 2 \cdot n ! U _ {n} ,\ \ U _ {n} = | \{ {s } : {\rho ( s , e ) = n , \rho ( s , c ) = n , s \in S _ {n} } \} | , $$
where $ e $ is the identity permutation and $ c = ( 1 \dots n ) $. The following formula has been obtained:
$$ U _ {n} = n ! \sum_{k=0}^ { n } ( - 1 ) ^ {k} \frac{2n}{2n-k} \left ( \begin{array}{c} 2n- k \\ k \end{array} \right ) ( n - k ) ! . $$
If
$$ U _ {n} ( s _ {1} , s _ {2} ) = \ | \{ {s } : {\rho ( s , s _ {1} ) = n , \rho ( s , s _ {2} ) = n ,\ s \in S _ {n} } \} | , $$
then $ U _ {n} ( s _ {1} , s _ {2} ) $ depends only on the cycle structure of $ s _ {1} ^ {-1} s _ {2} $ and can be expressed in the form of a formula with the use of Chebyshev polynomials (see [4]).
Closely related to the above problems is that of determining the number $ L _ {kn} $ of Latin rectangles (cf. Latin rectangle) of size $ k \times n $ and the number $ L _ {n} $ of Latin squares. A Latin $ ( k \times n ) $- rectangle can be regarded as an ordered collection of permutations $ s _ {1} \dots s _ {k} $ of degree $ n $ such that $ \rho ( s _ {i} , s _ {j} ) = n $, $ i \neq j $. It can be shown that
$$ L _ {1n} = n ! ,\ \ L _ {2n} = D _ {n} \cdot n ! ,\ D _ {n} = D _ {n0} , $$
$$ L _ {3 n } = n ! \sum_{k=0}^ { [ } n/2] \left ( \begin{array}{c} n \\ k \end{array} \right ) D _ {k} D _ {n-k} U _ {n-2k} ,\ U _ {0} = D _ {0} = 1 . $$
It has been established that for $ k < n ^ {1 / 3 - \epsilon } $, $ \epsilon > 0 $,
$$ L _ {kn} = ( n ! ) _ {k} \cdot e ^ {\left ( \begin{array}{c} k \\ 2 \end{array} \right ) } ( 1 + \delta _ {n} ) , $$
where $ \delta _ {n} \rightarrow 0 $ as $ n \rightarrow \infty $. The number of Latin squares of order $ n $ is known up to and including $ n = 9 $.
The problem of the number of additive partitions of a positive integer $ n $ first appeared in a latter form G. Leibniz to J. Bernoulli in 1669. However, the development of methods for solving an entire class of such problems was effected by Euler, who effectively used for this purpose generating functions in the form of infinite products. In particular, he showed that the number of partitions of $ m + n $ into $ n $ summands is equal to the number of partitions of $ m $ into at most $ n $ summands, which is the same as the number of partitions of $ m $ into summands none of which exceeds $ n $, and is also equal to the number of partitions of
$$ m + \left ( \begin{array}{c} n+ 1 \\ 2 \end{array} \right ) $$
into $ n $ distinct summands.
The classical allocation problem consists in determining the number $ C _ {nm} ( r) $ of ways of placing $ m $ different objects into $ n $ different cells with a given number $ r $ of empty cells. It can be shown that
$$ C _ {nm} ( r) = \ \left ( \begin{array}{c} n \\ r \end{array} \right ) \Delta ^ {n-r} 0 ^ {m} ,\ \ r = 0 \dots n , $$
where
$$ \Delta ^ {k} 0 ^ {m} = \sum_{j=0}^ { k } ( - 1 ) ^ {j} \left ( \begin{array}{c} k \\ j \end{array} \right ) ( k - j ) ^ {m} . $$
The investigations here have been carried out in the setting of probability-theoretic applications including various generalizations and modifications. The most interesting part of these investigations touches upon the achievement of various asymptotic results when $ m $ and $ n $ increase without bound.
References
| [1] | M.M. Postnikov, "Magic squares" , Moscow (1964) (In Russian) |
| [2] | M. Hall, "Combinatorial theory" , Blaisdell (1967) Zbl 0196.02401 |
| [3] | O. Ore, "Theory of graphs" , Amer. Math. Soc. (1962) Zbl 0105.35401 |
| [4] | J. Riordan, "An introduction to combinatorial analysis" , Wiley (1958) Zbl 0078.00805 |
| [5] | F. Harary, "Graph theory" , Addison-Wesley (1969) pp. Chapt. 9 |
| [a1] | H.J. Ryser, "Combinatorial mathematics" , Carus Math. Monogr. , 14 , Math. Assoc. Amer. (1963) |
Classical combinatorial problems. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Classical_combinatorial_problems&oldid=55086