Synthetic differential geometry

Geometers like S. Lie, E. Cartan and their contemporaries explicitly used infinitesimal real numbers, infinitesimal curves, etc. and Lie referred to methods based on infinitesimals as "synthetic" , as opposed to "analytic" (cf. [a1]). In present day mathematics, based on set-theoretic foundations, such infinitesimal reals do not exist, and the synthetic methods cannot be made mathematically rigorous in a direct way.

The phrase "synthetic differential geometry" usually refers to a development initiated by F.W. Lawvere's 1967 lecture (later published as [a2]). This development is based on category-theoretic rather than set-theoretic foundations, and is compatible with infinitesimals. For example, one of the basic axioms (often called the Kock–Lawvere axiom) states that for the subobject $ D= \{ x : x ^ {2} = 0 \} $ of the line $ \mathbf R $ the mapping $ \mathbf R \times \mathbf R \rightarrow \mathbf R ^ {D} $, sending $ ( a, b) $ to the "infinitesimal" straight line $ ax+ b $, is an isomorphism. Thus, the derivative of a function $ f: \mathbf R \rightarrow \mathbf R $ at a point $ t \in \mathbf R $ can be defined in a purely algebraic way as the unique number $ f ^ { \prime } ( t) $ for which $ f( t+ x)= f ^ { \prime } ( t)+ x \cdot f ^ { \prime } ( t) $ for all $ x \in D $; no limits are involved in this definition. Much of "infinitesimal" differential geometry, such as the theory of connections, curvature, etc., can be similarly developed in a purely algebraic fashion, by explicitly using infinitesimals. It is remarkable that in the context of synthetic differential geometry infinitesimal arguments such as those by Cartan literally make sense, and are mathematically rigorous.

The relation with ordinary differential geometry is established via suitable models, as presented in [a3] and [a4]. These models are Grothendieck topoi (cf. Topos), much like the ones in algebraic geometry, but based on rings of smooth functions on manifolds, and quotients of such rings by ordinary ideals.

Following Lawvere, every topos can be viewed as a universe of sets, with an intrinsic logic which is intuitionistic. Thus, it is possible to give foundations of synthetic differential geometry which are based on intuitionistic set theory rather than on category theory (this is done in [a5]).

It should be emphasized that the infinitesimals used in synthetic differential geometry are generally nilpotent, and hence cannot be accounted for in Robinson's non-standard analysis. The compatibility of non-standard analysis with synthetic differential geometry is demonstrated in [a4].

For detailed expositions of various aspects of synthetic differential geometry see [a5], [a7], [a8].

References

[a1]	S. Lie, "Allgemeine Theorie der partiellen Differentialgleichungen erster Ordnung" Math. Ann. , 9 (1876) pp. 245–296 MR1509861 Zbl 09.0261.01 Zbl 07.0225.01
[a2]	F.W. Lawvere, "Categorical dynamics" A. Kock (ed.) , Topos theoretic methods in geometry , Aarhus Univ. (1979) pp. 1–28 MR0552656 Zbl 0403.18005
[a3]	E. Dubuc, "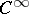-schemes" Amer. J. Math. , 103 (1981) pp. 683–690 MR0623133 Zbl 0483.58003
[a4]	I. Moerdijk, G.E. Reyes, "A smooth version of the Zariski topos" Adv. Math. , 65 (1987) pp. 229–253 MR0904724 Zbl 0648.18006
[a5]	R. Lavendhomme, "Leçons de la géométrie différentielle synthétique naive" , Univ. Louvain (1987)
[a6]	A. Robinson, "Non-standard analysis" , North-Holland (1966) MR0205854 Zbl 0151.00803
[a7]	A. Kock, "Synthetic differential geometry" , Cambridge Univ. Press (1981) MR0649622 MR0596153 Zbl 0487.18006 Zbl 0466.51008
[a8]	I. Moerdijk, G.E. Reyes, "Models for smooth infinitesimal analysis" , Springer (1991) MR1083355 Zbl 0715.18001