Subtangent and subnormal
The directed segments $ QT $
and $ QN $
which are the projections on the $ x $-
axis of the segments of the tangent line $ MT $
and the normal $ MN $
to a certain curve at a point $ M $(
see Fig.).
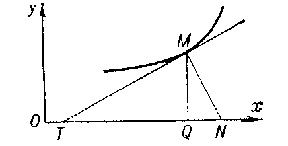
Figure: s091040a
If the curve is the graph of a function $ y = f( x) $, the values of the subtangent and subnormal are equal to
$$ QT = - \frac{f( x) }{f ^ { \prime } ( x) } ,\ \ ON = f( x) f ^ { \prime } ( x), $$
respectively, where $ x $ is the abscissa of the point $ M $. If the curve is given parametrically by
$$ x = \phi ( t),\ y = \psi ( t), $$
then
$$ QT = - \frac{\psi ( t) \phi ^ \prime ( t) }{\psi ^ \prime ( t) } ,\ \ QN = \frac{\psi ( t) \psi ^ \prime ( t) }{\psi ^ \prime ( t) } , $$
where $ t $ is the value of the parameter defining the point $ M $ on the curve.
References
| [a1] | M. Berger, "Geometry" , II , Springer (1989) |
| [a2] | F. Gomes Teixeira, "Traité des courbes" , 1–3 , Chelsea, reprint (1971) |
| [a3] | H. Lamb, "Infinitesimal calculus" , Cambridge (1924) pp. 118 |
Subtangent and subnormal. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Subtangent_and_subnormal&oldid=53941