Selection theorems

A group of theorems in combinatorial theory related to the selection of elements from a set which in some way correspond to a family of subsets of that set. Selection theorems are commonly employed as existence theorems in solving various combinatorial problems. Below some of the most important selection theorems are listed, and examples of their application are given.

1) Let $ S = \{ S _ {1} \dots S _ {n} \} $ be some family of subsets of a given set $ T = \{ t _ {1} \dots t _ {m} \} $. A sample $ R = \{ t _ {i _ {1} } \dots t _ {i _ {n} } \} $ of distinct elements of the set $ T $ is called a system of distinct representatives (cf. System of different representatives) of the family $ S $ if $ t _ {i _ {j} } \in S _ {j} $, $ j = 1 \dots n $; the element $ t _ {i _ {j} } $ is a representative of the set $ S _ {j} $. For example, if $ T = \{ 1, 2, 3, 4, 5 \} $ and $ S $ consists of $ S _ {1} = \{ 2, 4, 5 \} $, $ S _ {2} = \{ 2, 5 \} $, $ S _ {3} = \{ 3, 4 \} $, $ S _ {4} = \{ 1, 3, 4 \} $, then $ R = \{ 5, 2, 3, 4 \} $ is a system of distinct representatives of $ S $, where the element 5 represents the set $ S _ {1} $, the element 2 represents set $ S _ {2} $, etc. If, on the other hand, $ S $ is composed of sets $ S _ {1} = \{ 2, 4, 5 \} $, $ S _ {2} = \{ 2, 5 \} $, $ S _ {3} = \{ 4, 5 \} $, $ S _ {4} = \{ 2, 4 \} $, $ S $ will have no system of distinct representatives, since $ S _ {1} , S _ {2} , S _ {3} , S _ {4} $ together contain only three elements.

The theorem on a system of distinct representatives: A family $ S = \{ S _ {1} \dots S _ {n} \} $ has a system of distinct representatives if and only if the union of any $ k $ sets of $ S $ contains at least $ k $ distinct elements, where $ k = 1 \dots n $.

This theorem was proved by Ph. Hall [3] (see also [1], [2]). It may be used to prove the theorem on common representatives, which is also a selection theorem. Let

$$ \tag{1 } T = A _ {1} \cup \dots \cup A _ {l} , $$

$$ \tag{2 } T = B _ {1} \cup \dots \cup B _ {l} $$

be two partitions of the set $ T $, i.e. none of the components is empty and $ A _ {i} \cap A _ {j} = B _ {i} \cap B _ {j} = \emptyset $ if $ i \neq j $. The set $ R = \{ t _ {i _ {1} } \dots t _ {i _ {l} } \} $ is called a system of common representatives of the partitions (1) and (2) if $ R $ is a system of distinct representatives both for the family $ A = \{ A _ {1} \dots A _ {l} \} $ and the family $ B = \{ B _ {1} \dots B _ {l} \} $. For instance, if $ T = \{ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 \} $ and if

$$ T = A _ {1} \cup A _ {2} \cup A _ {3} \cup A _ {4} , $$

$$ T = B _ {1} \cup B _ {2} \cup B _ {3} \cup B _ {4} $$

are two partitions of $ T $, where $ A _ {1} = \{ 0, 1, 2, 3 \} $, $ A _ {2} = \{ 4, 5, 6 \} $, $ A _ {3} = \{ 7 \} $, $ A _ {4} = \{ 8, 9 \} $, $ B _ {1} = \{ 4, 7, 8 \} $, $ B _ {2} = \{ 0, 5 \} $, $ B _ {3} = \{ 2, 3, 6 \} $, $ B _ {4} = \{ 1, 9 \} $, then $ R = \{ 0, 6, 7, 9 \} $ is a system of common representatives of the families $ A = \{ A _ {1} , A _ {2} , A _ {3} , A _ {4} \} $ and $ B = \{ B _ {1} , B _ {2} , B _ {3} , B _ {4} \} $ since it is a system of distinct representatives for both $ A $ and $ B $; here the element 0 represents the sets $ A _ {1} $ and $ B _ {2} $, the element 6 represents $ A _ {2} $ and $ B _ {3} $, the element 7 represents $ A _ {3} $ and $ B _ {1} $, while the element 9 represents $ A _ {4} $ and $ B _ {4} $.

The theorem on a system of common representatives: The partitions (1) and (2) have a system of common representatives if and only if the union of any $ k $ sets of $ A $ contains at most $ k $ sets from the family $ B $, $ k = 1 \dots l $[1], [2].

2) Let there be given a rectangular matrix. The term line will denote both a row and a column of this matrix.

König's theorem: If the elements of a rectangular matrix are zeros and ones, the minimum number of lines containing all ones is equal to the maximum number of ones which may be selected so that no two of them are located on the same line.

This theorem was formulated and proved by D. König ([4], see also [1], [2]). It is equivalent to the Ph. Hall theorem. It is employed, for example, in order to prove that certain matrices are linear combinations of permutation matrices (a permutation matrix is a rectangular matrix $ P $ of dimension $ m \times n $, consisting of zeros and ones, such that $ P P ^ \prime = I $, where $ P ^ \prime $ is the transposed matrix of $ P $ and $ I $ is the identity matrix of order $ m $; for example, a square permutation matrix of order $ m $ consists of $ m $ ones which are so disposed that no two of them lie on the same line). In other words, if a matrix $ A $ of dimension $ m \times n $, $ m \leq n $, has been given, with non-negative real numbers as its elements and such that the sum of the elements of each row in $ A $ is $ m ^ \prime $ and the sum of the elements of each column is $ n ^ \prime $, then

$$ A = c _ {1} P _ {1} + \dots + c _ {t} P _ {t} , $$

where each $ P _ {i} $ is a permutation matrix, while the coefficients $ c _ {i} $ are non-negative real numbers [1], [2]. In particular, if a square matrix $ A $ of order $ n $, consisting of zeros and ones, is such that the sum of the elements in any column or any row is equal to a positive integer $ k $, then

$$ A = P _ {1} + \dots + P _ {k} , $$

where all $ P _ {i} $ are permutation matrices of order $ n $.

Let $ T $ be a finite set and let $ P _ {r} ( T) $ be the set of all its subsets containing exactly $ r $ elements. Let

$$ \tag{3 } P _ {r} ( T) = A _ {1} \cup \dots \cup A _ {l} $$

be an arbitrary ordered partition of $ P _ {r} ( T) $ into $ l $ components $ A _ {1} \dots A _ {l} $. Let $ q _ {1} \dots q _ {l} $ be integers such that

$$ \tag{4 } 1 \leq r \leq q _ {1} \dots q _ {l} . $$

If there exists a subset, containing $ q _ {i} $ elements of the set $ T $, such that all its subsets containing exactly $ r $ elements are contained in $ A _ {i} $, it is said to be a $ ( q _ {i} , A _ {i} ) $- subset of the set $ T $.

Ramsey's theorem: Let there be given integers $ q _ {1} \dots q _ {l} $ and $ r $ which satisfy condition (4). Then there exists a natural number $ N ( q _ {1} \dots q _ {l} , r ) $ such that for any integer $ n \geq N ( q _ {1} \dots q _ {l} , r ) $ the following assertion is valid: Given a set $ T $ of $ n $ elements and an arbitrary ordered partition (3) of the set $ P _ {r} ( T) $ into $ l $ components $ A _ {1} \dots A _ {l} $, then $ T $ will contain a $ ( q _ {i} , A _ {i} ) $- subset for some $ i = 1 \dots l $.

This theorem was proved by F. Ramsey [5]; see also [1], [2]. An example of an application of this theorem is the following result [6], [1], [2]: For any given integer $ m \geq 3 $ there exists an integer $ N _ {m} $ such that out of $ n \geq N _ {m} $ points in a plane no three of which lie on a straight line, there are $ m $ points which form a convex $ m $- gon.

References

[1]	M. Hall, "Combinatorial theory" , Blaisdell (1967)
[2]	H.J. Ryser, "Combinatorial mathematics" , Carus Math. Monogr. , 14 , Math. Assoc. Amer. (1963)
[3]	Ph. Hall, "On representatives of subsets" J. London Math. Soc. , 1 (1935) pp. 26–30
[4]	D. König, "Theorie der endlichen und unendlichen Graphen" , Chelsea, reprint (1950)
[5]	F.P. Ramsey, "On a problem of formal logic" Proc. London Math. Soc. (2) , 30 (1930) pp. 264–286
[6]	P. Erdös, G. Szekeres, "A combinatorial problem in geometry" Compositio Math. , 2 (1935) pp. 463–470

Comments

The popular name of the Ph. Hall theorem is marriage theorem or Ph. Hall marriage theorem.

An ordered partition of $ P _ {r} ( T) $( as in (3)) can be regarded as a colouring of $ P _ {r} ( T) $( with $ l $ colours).

An important selection theorem is Rado's selection principle, see [a1]–[a3].

Selection problems and theorems arise in many parts of mathematics, not only combinatorics. The general setting is that of a set-valued mapping $ F: T \rightarrow 2 ^ {X} $( where $ 2 ^ {X} $ is the set of all subsets of $ X $) and the problem is to find a selection $ f: T \rightarrow X $ such that $ f ( t) \in F( t) $ for all $ t $. Such a function $ f $ is sometimes called a selector.

Note that the axiom of choice is an assertion about the existence of selections.

Further selection problems occur in topology, game theory, probability, measure theory, analysis, etc. A selection follows.

The Kuratowski–Ryll-Nardzweski selection theorem, [a1], says the following. Let $ X $ be a space with a $ \sigma $- algebra of subsets $ S $( cf. Algebra of sets) and let $ Y $ be a complete separable metric space. Let $ F $ be a measurable set-valued function on $ X $ to the closed non-empty subsets of $ Y $. Here, measurable means that $ \{ {x } : {F( x) \cap U \neq \emptyset } \} $ is in $ S $ for every open $ U \subset Y $. Then there exists a measurable selector $ f : X \rightarrow Y $( i.e. such that $ f ^ { - 1 } ( U) \in S $ for every open $ U \subset Y $).

The von Neumann measurable choice theorem, [a2], says essentially the following. Let $ Y $ be a complete separable metric space and $ F: [ 0, 1] \rightarrow Y $ an analytic set-valued function. Then there is a Lebesgue-measurable selector $ f: [ 0, 1] \rightarrow Y $. Here, the set-valued function $ F $ on $ [ 0, 1] $ is called analytic if its graph $ \{ {( t, u) \in [ 0, 1] \times Y } : {u \in F( t) } \} $ is an analytic subset of $ [ 0, 1] \times Y $( cf. Analytic set).

In topology there is, for example, Michael's continuous selection theorem, [a3], which characterizes paracompactness: A $ T _ {1} $- space $ X $ is paracompact if and only if every lower semi-continuous mapping $ F $ on $ X $ with values in the closed convex non-empty subsets of a Banach space $ Y $ admits a continuous selector.

Cf. [a4], [a5] for some more selection theorems, more details and applications. For some other (variants of) selection theorems cf. also Multi-valued mapping. The phrase "selection theorem" is also used for various results pertaining e.g. to the selection of converging subsequences, cf. e.g. Helly theorem; Blaschke selection theorem; Bolzano–Weierstrass selection principle.

References

[a1]	K. Kuratowski, C. Ryll-Nardzweski, "A general theorem on selectors" Bull. Acad. Pol. Sci., Ser. Math. Astron. Phys. , 13 (1965) pp. 397–403
[a2]	J. von Neumann, "On rings of operators. Reduction theory" Ann. of Math. , 50 (1949) pp. 448–451
[a3]	E. Michael, "Continuous selections I" Ann. of Math. , 63 (1956) pp. 361–382
[a4]	T. Parthasarathy, "Selection theorems and their applications" , Lect. notes in math. , 263 , Springer (1972)
[a5]	W.M. Fleischman (ed.) , Set valued mappings, selections and topological properties of 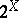(Proc. Conf. SUNY Buffalo, 1969) , Lect. notes in math. , 171 , Springer (1970)
[a6]	L. Mirsky, "Transversal theory" , Acad. Press (1971)
[a7]	H. Lüneburg, "Tools and fundamental constructions of combinatorial mathematics" , B.I. Wissenschaftsverlag Mannheim (1989)
[a8]	R.L. Graham, B.L. Rothschild, J.H. Spencer, "Ramsey theory" , Wiley (Interscience) (1980)