Multi-valued mapping

point-to-set mapping

A mapping $\Gamma : X \rightarrow Y$ associating with each element $x$ of a set $X$ a subset $\Gamma ( x)$ of a set $Y$. If for each $x \in X$ the set $\Gamma ( x)$ consists of one element, then the mapping $\Gamma$ is called single-valued. A multi-valued mapping $\Gamma$ can be treated as a single-valued mapping of $X$ into $2 ^ {Y}$, that is, into the set of all subsets of $Y$.

For two multi-valued mappings $\Gamma _ {i} : X \rightarrow Y$, $i = 1 , 2$, their inclusion is naturally defined: $\Gamma _ {1} \subset \Gamma _ {2}$ if $\Gamma _ {1} ( x) \subset \Gamma _ {2} ( x)$ for all $x \in X$. For any family of multi-valued mappings $\Gamma _ \alpha : X \rightarrow Y$, $\alpha \in A$, the union and intersection are defined: $\Gamma = \cup _ {\alpha \in A } \Gamma _ \alpha$ if $\Gamma ( x) = \cup _ {\alpha \in A } \Gamma _ \alpha ( x)$ for all $x \in X$ and $\Gamma = \cap _ {\alpha \in A } \Gamma _ \alpha$ if $\Gamma ( x) = \cap _ {\alpha \in A } \Gamma _ \alpha ( x)$ for all $x \in X$. For any family of multi-valued mappings $\Gamma _ \alpha : X \rightarrow Y _ \alpha$, $\alpha \in A$, the multi-valued mapping $\Gamma = \prod _ {\alpha \in A } \Gamma _ \alpha : X \rightarrow \prod _ {\alpha \in A } Y _ \alpha$ is called the Cartesian product of the multi-valued mappings $\Gamma _ \alpha$ if $\Gamma ( x) = \prod _ {\alpha \in A } \Gamma _ \alpha ( x)$. A section of a multi-valued mapping $\Gamma$ is a single-valued mapping $f : X \rightarrow Y$ such that $f ( x) \in \Gamma ( x)$ for all $x \in X$. The graph of a multi-valued mapping $\Gamma$ is the set $G ( \Gamma ) = \{ {( x , y ) \in X \times Y } : {y \in \Gamma ( x) } \}$.

A multi-valued mapping $\Gamma$ of a topological space $X$ into a topological space $Y$ is called upper semi-continuous if for every open set $U \subset Y$ the set $\Gamma ^ {+} ( u) = \{ {x \in X } : {\Gamma ( x) \subset U, \Gamma ( x) \neq \emptyset } \}$ is open in $X$, or equivalently: For any $x \in X$ and any neighbourhood $U$ of $\Gamma ( x)$ there is a neighbourhood $O x$ of $x$ such that $\Gamma ( Ox) \subset U$, where $\Gamma ( Ox ) = \cup \{ {\Gamma ( y) } : {y \in Ox } \}$. A multi-valued mapping from a topological space $X$ to a topological space $Y$ is called lower semi-continuous if for any open set $U \subset Y$ the set $\Gamma ^ {-} ( U) = \{ {x \in X } : {\Gamma ( x) \cap U \neq \emptyset } \}$ is open in $X$. If a multi-valued mapping satisfies both properties simultaneously, then it is called a continuous multi-valued mapping.

Let $Y$ be a topological vector space. A multi-valued mapping $\Gamma : X\rightarrow Y$ is called convex-compact valued if $\Gamma ( x)$ is a convex compact set for all $x \in X$. For a finite set of multi-valued mappings $\Gamma _ {i} : X \rightarrow Y$, $i \in I$, the algebraic sum $\Gamma = \sum _ {i \in I } \Gamma _ {i}$ is defined by $\Gamma ( x) = \sum _ {i \in I } \Gamma _ {i} ( x)$. The intersection of any (finite) family of upper semi-continuous (respectively, continuous) multi-valued mappings is upper semi-continuous (respectively, continuous). The Cartesian product of a finite family of upper semi-continuous multi-valued mappings is upper semi-continuous. The algebraic sum of a finite family of upper semi-continuous (convex-compact valued) mappings is upper semi-continuous (convex-compact valued). The intersection and Cartesian product of any family of convex-compact valued mappings is convex-compact valued.

Let $X$ be a paracompact space and $Y$ a locally convex metric linear space (cf. Locally convex space; Linear space; Metric space). Let $\Gamma : X \rightarrow Y$ be a multi-valued mapping which is upper semi-continuous and is such that $\Gamma ( x)$ is closed in $Y$ for every $x \in X$. Then the multi-valued mapping $\Gamma$ admits continuous sections. Let $( X , \mathfrak A )$ and $( Y , \mathfrak B )$ be spaces with given $\sigma$- algebras $\mathfrak A$ and $\mathfrak B$; a multi-valued mapping $\Gamma : ( X , \mathfrak A ) \rightarrow ( Y , \mathfrak B )$ is called measurable if the graph $G ( \Gamma )$ belongs to the smallest $\sigma$- algebra $\mathfrak A \times \mathfrak B$ of $X \times Y$ containing all sets of the form $A \times B$, where $A \in \mathfrak A$ and $B \in \mathfrak B$. If $\Gamma$ is a measurable multi-valued mapping from $( X , \mathfrak A )$ to a complete separable metric space $( Y , \mathfrak B )$, where $\mathfrak B$ is the Borel $\sigma$- algebra of $Y$, then $\Gamma$ has measurable sections $f$.

References

[1]	K. Kuratowski, "Topology" , 1–2 , Acad. Press (1966–1968) (Translated from French)

Comments

A multi-valued mapping is also called a set-valued or many-valued mapping. Sections are also called selections.

Theorems which prove that certain kinds of multi-valued mappings admit selections are called selection theorems. The measurable selection theorem stated in the last sentence of the main article above is known as von Neumann's measurable choice theorem. A number of selection theorems and some applications are discussed in [a4].

References

[a1]	E. Michael, "Continuous selections" Ann. of Math. , 63 (1956) pp. 361–382
[a2]	E.A. Michael, "A survey of continuous selections" W.M. Fleischmann (ed.) , Set valued mappings, selections and topological properties of 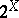(Proc. Conf. SUNY Buffalo, 1969) , Lect. notes in math. , 171 , Springer (1970) pp. 54–58
[a3]	K. Przeslawski, D. Yost, "Continuity properties of selectors and Michael's Theorem" Mich. Math. J. , 36 (1989) pp. 113–134
[a4]	T. Parthasarathy, "Selection theorems and their applications" , Lect. notes in math. , 263 , Springer (1972)