Ruled surface

A ruled surface in differential geometry is a surface formed by a motion of a straight line. The lines that belongs to this surface are called (rectilinear) generators, and every curve that intersects all the generators is called a directrix. If $ \rho = \rho ( v) $ is the position vector of the directrix and $ m = m ( v) $ is the unit vector of the generator passing through $ \rho ( v) $, then the position vector of the ruled surface is

$$ r( u, v) = \rho ( v) + u m ( v) , $$

where $ u $ is the coordinate of a point on the generator. The line element of the ruled surface is

$$ d s ^ {2} = d u ^ {2} + 2 ( m \rho ^ \prime ) du dv + ( \rho ^ {\prime 2 } + 2 ( m ^ \prime \rho ^ \prime ) u + m ^ {\prime 2 } u ^ {2} ) d v ^ {2} . $$

A ruled surface is characterized by the fact that its asymptotic net is semi-geodesic. A ruled surface can always be bent in a unique way so that an arbitrary curve on it becomes asymptotic (Beltrami's theorem). Moreover, if a ruled surface that is not developable is bent into another ruled surface, then either their generators coincide or they can both be bent into a quadric on which the net corresponding to the families of generators is asymptotic (Bonnet's theorem).

The set of points of a ruled surface at which the geodesic curvature of the orthogonal trajectories of the generators vanishes is called the line of striction of the ruled surface (or line of contraction, since through each point of it, a point of striction, in the limit there passes the common perpendicular of two infinitely close generators). The coordinate of a point of striction is $ u = -( \rho ^ \prime m ^ \prime ) / m ^ \prime 2 $; on a cylinder the line of striction is undefined, and on a developable surface it is the edge of regression. The limit $ p $ of the ratio of the shortest distance between two infinitely-close generators of a ruled surface to the angle between them is called the distribution parameter of the ruled surface: $ p = ( m m ^ \prime \rho ) / m ^ \prime 2 $; a developable surface is characterized by the fact that $ p = 0 $ for it. The Gaussian curvature of a ruled surface is

$$ K = - \frac{p ^ {2} ( m ^ \prime ) ^ {2} } \gamma , $$

where

$$ \gamma = \rho ^ \prime 2 + 2 u ( \rho ^ \prime m ^ \prime ) + u ^ {2} m ^ \prime 2 - ( \rho ^ \prime m ) ^ {2} . $$

The only minimal ruled surface is the helicoid. A ruled surface of revolution is a one-sheet hyperboloid, possibly degenerating to a cylinder, a cone or a plane. If all the generators of a ruled surface are parallel to one plane, then the surface is a Catalan surface.

References

[1]	V.F. Kagan, "Foundations of the theory of surfaces in a tensor setting" , 1–2 , Moscow-Leningrad (1947–1948) (In Russian)
[2]	V.I. Shulikovskii, "Classical differential geometry in a tensor setting" , Moscow (1963) (In Russian)
[3]	P.K. Rashevskii, "A course of differential geometry" , Moscow (1956) (In Russian)

References

[a1]	H. Brauner, "Differentialgeometrie" , Vieweg (1981) MR0616082 Zbl 0466.53001
[a2]	J. Hoschek, "Liniengeometrie" , B.I. Wissenschaftverlag Mannheim (1971) MR0353164 Zbl 0227.53007
[a3]	M. Berger, B. Gostiaux, "Differential geometry: manifolds, curves, and surfaces" , Springer (1988) (Translated from French) MR0917479 Zbl 0629.53001
[a4]	G. Darboux, "Leçons sur la théorie générale des surfaces et ses applications géométriques du calcul infinitésimal" , 1–4 , Chelsea, reprint (1972)
[a5]	M.P. Do Carmo, "Differential geometry of curves and surfaces" , Prentice-Hall (1976) pp. 145 Zbl 0326.53001

A ruled surface in algebraic geometry is a smooth projective surface $ F $ over an algebraically closed field $ k $ that is birationally equivalent to a surface $ P ^ {1} \times C $, where $ P ^ {1} $ is the projective line and $ C $ is a smooth projective curve of genus $ g \geq 0 $. An example of a ruled surface is the projectivization $ P _ {C} ( {\mathcal E} ) $ of a sheaf $ {\mathcal E} $ of rank 2 on $ C $ that is locally free in the Zariski topology.

If there is a smooth morphism $ p : F \rightarrow C $ each fibre of which is isomorphic to $ P ^ {1} $, then $ F $ is called a geometrically-ruled surface with base $ C $. When $ C $ is a curve of genus $ 0 $, a geometrically-ruled surface is called a rational ruled surface; when the genus of $ C $ is equal to $ g \geq 1 $, it is called a geometrically-ruled surface of genus $ g $. By the Noether–Enriques theorem, the morphism $ p $ always has a section $ s : C \rightarrow F $( see [1], [2], [5]).

The properties of a ruled surfaces are as follows (see [1], [2], [6]): a) Every geometrically-ruled surface $ F $ with base $ C $ has the form $ P _ {C} ( {\mathcal E} ) $, where $ {\mathcal E} $ is a locally free sheaf of rank 2 on $ C $, and

$$ P _ {C} ( {\mathcal E} ) \cong P _ {C} ( {\mathcal E} ^ \prime ) $$

over $ C $ if and only if there is an invertible sheaf $ {\mathcal L} $ on $ C $ such that $ {\mathcal E} \cong {\mathcal E} ^ \prime \otimes {\mathcal L} $.

b) All rational geometrically-ruled surfaces are exhausted up to an isomorphism by the countable series of surfaces

$$ F _ {n} = P _ {P ^ {1} } ( {\mathcal O} _ {P ^ {1} } \oplus {\mathcal O} _ {P ^ {1} } ( n) ) , $$

where $ n \geq 0 $ is an integer and $ {\mathcal O} _ {P ^ {1} } ( n) $ is an invertible sheaf on $ P ^ {1} $ of degree $ n $; except for the Veronese surface $ V _ {4} \subset P ^ {5} $( cf. Veronese mapping), all surfaces of degree $ n $ in $ P ^ {n+} 1 $ are rational geometrically-ruled surfaces or cones over normal rational curves.

c) If $ F $ is a minimal smooth projective surface over $ k $ that is birationally equivalent to $ P ^ {1} \times C $, where $ C $ is a curve of genus $ g \geq 1 $, then $ F $ is a geometrically-ruled surface with base $ C $, and $ C $ is uniquely determined by $ F $ up to an isomorphism.

d) If $ F $ is a geometrically-ruled surface with base $ C $ and $ p : F \rightarrow C $ is the corresponding morphism, then

$ \mathop{\rm Pic} ( F ) \cong p ^ {*} \mathop{\rm Pic} ( C) \oplus \mathbf Z ^ {S} $, where $ S $ is the class of some section; and

$ q ( F ) = g $, $ P _ {g} ( F ) = 0 $, $ P _ {n} ( F ) = 0 $ for any $ n \geq 2 $, and

$$ K _ {F} ^ {2} = 8 ( 1 - g ) , $$

where $ g $ is the genus of $ C $, $ q ( F ) = \mathop{\rm dim} H ^ {1} ( F , {\mathcal O} _ {F} ) $ is the irregularity, $ P _ {g} ( F ) = \mathop{\rm dim} H ^ {2} ( F , {\mathcal O} _ {F} ) $ is the geometric genus, $ P _ {n} ( F ) = \mathop{\rm dim} H ^ {0} ( F , {\mathcal O} _ {F} ( n K _ {F} ) ) $ is the $ n $- fold genus, and $ K _ {F} $ is the canonical divisor of $ F $.

e) If $ F $ is a geometrically-ruled surface with base $ C $ and $ S $ is the class of some section of the morphism $ p : F \rightarrow C $, then there is an invertible sheaf $ {\mathcal L} $ on $ C $ such that the invertible sheaf $ {\mathcal M} = {\mathcal O} _ {F} ( S) \otimes p ^ {*} {\mathcal L} $ determines an isomorphic imbedding $ \phi _ {\mathcal M} : F \rightarrow P ^ {N} $ for which the fibres of $ p $ are mapped onto straight lines lying on $ F ^ { \prime } = \phi _ {\mathcal M} ( F ) $ and covering $ F ^ { \prime } $, that is, $ F ^ { \prime } $ is a ruled surface in the usual sense.

Ruled surfaces form a distinguished class in the Enriques classification of algebraic surfaces (see [1], [2], [3]). They are characterized by any of the following criteria for being ruled (see [1], [3], [4], [5], [7]):

$ \alpha $) The Kodaira dimension $ \kappa ( F ) = - \infty $.

$ \beta $) The $ n $- fold genus $ P _ {n} ( F ) = 0 $ for $ n = 12 $.

$ \gamma $) For some (equivalently, for any) minimal model $ F ^ { * } $ of $ F $ the condition for termination of adjunction is satisfied, that is, for any divisor $ D \in \mathop{\rm Div} ( F ^ { * } ) $ there is an integer $ n _ {0} $ such that the linear system $ | D + n K _ {F} | $ is empty for all $ n \geq n _ {0} $, where $ K _ {F} $ is the canonical divisor.

$ \delta $) On some (equivalently, on any) minimal model $ F ^ { * } $ there is a curve $ E $ with $ ( E \cdot K _ {F ^ { * } } ) < 0 $.

References

[1]	I.R. (ed.) Shafarevich, "Algebraic surfaces" Proc. Steklov Inst. Math. , 75 (1965) Trudy Mat. Inst. Akad. Nauk SSSR , 75 (1965) MR1392959 MR1060325 Zbl 0154.21001
[2]	A. Beauville, "Surfaces algébriques complexes" Astérisque , 54 (1978) MR0485887 Zbl 0394.14014
[3]	D. Husemoller, "Classification and embeddings of surfaces" R. Hartshorne (ed.) , Algebraic geometry (Arcata, 1974) , Proc. Symp. Pure Math. , 29 , Amer. Math. Soc. (1975) pp. 329–420 MR0506292 Zbl 0326.14009
[4]	E. Bombieri, D. Mumford, "Enriques' classification of surfaces in char 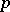. II" W.L. Baily jr. (ed.) T. Shioda (ed.) , Complex Analysis and Algebraic geometry , Cambridge Univ. Press & Iwanami Shoten (1977) pp. 23–42 MR0491719 MR0491720
[5]	F. Enriques, "Lezioni sulla teoria geometrica delle superficie algebriche" , CEDAM (1932)
[6]	R. Hartshorne, "Algebraic geometry" , Springer (1977) MR0463157 Zbl 0367.14001
[7]	K. Kodaira, "On the structure of complex analytic surfaces IV" Amer. J. Math. , 90 : 4 (1968) pp. 1048–1066 MR0239114 Zbl 0193.37702

V.A. Iskovskikh

References

[a1]	W. Edge, "The theory of ruled surfaces" , Cambridge Univ. Press (1931) MR1522836 Zbl 0001.40405 Zbl 57.0842.05
[a2]	A. van de Ven, "Compact complex surfaces" , Springer (1984) Zbl 0718.14023