Plancherel formula

A formula expressing the invariance of the inner product under Fourier transformation (cf. Fourier transform) on the space $ L _ {2} ( X) $:

$$ \int\limits _ { Y } \widehat{f} _ {1} ( y) \overline{ {\widehat{f} _ {2} ( y) }}\; d \mu ( y) = \int\limits _ { X } f _ {1} ( x) \overline{ {f _ {2} ( x) }}\; d \mu ( x). $$

In the classical case, where $ X = Y = \mathbf R ^ {n} $ is $ n $- dimensional Euclidean space and $ \mu ( x) $ and $ \mu ( y) $ denote $ n $- dimensional Lebesgue measure, the Fourier transformation

$$ f( x) \mapsto \widehat{f} ( y) $$

on $ L _ {2} ( \mathbf R ^ {n} ) $ is a continuous extension of the classical Fourier transformation

$$ g( x) \mapsto \widehat{g} ( y) = \frac{1}{( 2 \pi ) ^ {n/2} } \int\limits _ {\mathbf R ^ {n} } g( x) e ^ {i( x, y) } dx, $$

$$ g \in L _ {1} ( \mathbf R ^ {n} ) ,\ x = ( x _ {1} \dots x _ {n} ) ,\ y = ( y _ {1} \dots y _ {n} ), $$

where $ ( x, y) $ is the inner product in $ \mathbf R ^ {n} $, from the set $ L _ {1} ( \mathbf R ^ {n} ) \cap L _ {2} ( \mathbf R ^ {n} ) $ to the space $ L _ {2} ( \mathbf R ^ {n} ) $.

Plancherel's formula applies also when $ X $ is a locally compact commutative topological group, with $ Y $ its character group, $ x \in X $, $ y \in Y $, $ \mu ( x) $ and $ \mu ( y) $ are correspondingly normalized invariant measures (cf. Invariant measure) on $ X $ and $ Y $, and the Fourier transformation $ f( x) \mapsto \widehat{f} ( y) $ on the space $ L _ {2} ( X) $ is a continuous extension of the mapping

$$ g( x) \mapsto \widehat{g} ( y) = \int\limits _ { X } g( x) y( x) d \mu ( x), $$

$$ g( x) \in L _ {1} ( X) ,\ y( x) \in Y, $$

from the set $ L _ {1} ( X) \cap L _ {2} ( X) $ to the space $ L _ {2} ( Y) $.

Plancherel's formula can be extended to non-commutative topological groups. Let, e.g., $ G $ be a compact Hausdorff group, let $ \mu $ be an invariant measure on it, $ \mu ( G) = 1 $, let $ g \mapsto U _ {g} ^ {( \alpha ) } $ be an irreducible finite-dimensional unitary representation of dimension $ n _ \alpha $ of $ G $ in a Hilbert space (cf. Representation of a compact group), $ g \in G $, $ \alpha = 1, 2 \dots $ $ x( g) \in L _ {2} ( G) $, let

$$ T _ {x} ^ {( \alpha ) } = \int\limits _ { G } x( g) U _ {g} ^ {( \alpha )* } d \mu ( g) $$

(* denotes transition to the adjoint operator), and let $ \mathop{\rm Tr} ( T _ {x} ^ {( \alpha ) } T _ {x} ^ {( \alpha )* } ) $ be the trace of the operator $ T _ {x} ^ {( \alpha ) } T _ {x} ^ {( \alpha )* } $. Then the generalized Plancherel formula is:

$$ \tag{* } \int\limits _ { G } | x( g) | ^ {2} d \mu ( g) = \sum _ \alpha n _ \alpha \mathop{\rm Tr} ( T _ {x} ^ {( \alpha ) } T _ {x} ^ {( \alpha )* } ). $$

References

[1]	A.N. Kolmogorov, S.V. Fomin, "Elements of the theory of functions and functional analysis" , 1–2 , Graylock (1957–1961) (Translated from Russian)
[2]	M.A. Naimark, "Normed rings" , Reidel (1984) (Translated from Russian)

Comments

See also the references to Fourier transform. In the case of a locally compact unimodular type-I group there is a Plancherel formula quite analogous to (*), cf. [a3], § 18.8: just replace in (*) $ \sum _ \alpha n _ \alpha $ by an integral $ \int _ {\widehat{G} } d \nu ( \alpha ) $ over the unitary dual $ \widehat{G} $ of $ G $. In general, this formula is only available in abstract form. It is an important area of research to obtain more information about the Plancherel measure $ \nu $, such as its support, its discrete part and its full explicit expression. In the case of a real non-compact semi-simple Lie group this program was successfully completed by Harish-Chandra. More generally, Plancherel formulas can be considered on homogeneous spaces, for instance pseudo-Riemannian ones, cf. [a1], § II.2. Specialization of Plancherel formulas on groups or homogeneous spaces to functions satisfying certain covariance properties with respect to a subgroup may yield Plancherel formulas for integral transforms with special function kernels. The resulting Plancherel measure can often be alternatively interpreted as the spectral measure for an eigen value problem involving ordinary or partial differential operators.

References

[a1]	M. Flensted-Jensen, "Analysis on non-Riemannian symmetric spaces" , Amer. Math. Soc. (1986)
[a2]	H. Reiter, "Classical harmonic analysis and locally compact groups" , Clarendon Press (1968)
[a3]	J. Dixmier, "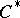 algebras" , North-Holland (1977) (Translated from French)
[a4]	E. Hewitt, K.A. Ross, "Abstract harmonic analysis" , 2 , Springer (1979)