Partial geometry
An incidence structure (cf. Incidence system) $ S = ( P , L , I ) $
in which the incidence relation between points and lines is symmetric and satisfies the following axioms:
1) each point is incident to $ r $ lines, $ r \geq 2 $, and two distinct points are incident to at most one line;
2) each line is incident to $ k $ points, $ k \geq 2 $;
3) through each point not incident to a line $ l $ there are exactly $ t \geq 1 $ lines intersecting $ l $.
If a partial geometry consists of $ v $ points and $ b $ lines, then
$$ v = \frac{k [ ( k - 1 ) ( r - 1 ) + t ] }{t} \ \textrm{ and } \ \ b = \frac{r [ ( k - 1 ) ( r - 1 ) + t ] }{t} , $$
and necessary conditions for the existence of such a partial geometry are that $ ( k - 1 ) ( r - 1 ) k r $ be divisible by $ t ( k + r - t - 1 ) $, $ k ( k - 1 ) ( r - 1 ) $ by $ t $ and $ r ( k - 1 ) ( r - 1 ) $ by $ t $( cf. [2]).
Partial geometries can be divided into four classes:
a) partial geometries with $ t = k $ or (dually) $ t = r $. Geometries of this type are just $ 2 - ( v , k , 1 ) $- schemes or $ 2 - ( v , r , 1 ) $- schemes (cf. Block design);
b) partial geometries with $ t = k - 1 $ or (dually) $ t = r - 1 $. In this case a partial geometry is the same thing as a net of order $ k $ and defect $ k - r + 1 $( or dually);
c) partial geometries with $ t = 1 $, known as generalized quadrangles;
d) partial geometries with $ 1 < t < \min ( k - 1 , r - 1 ) $.
References
| [1] | R.C. Bose, "Strongly regular graphs, partial geometries and partially balanced designs" Pacific J. Math. , 13 : 2 (1963) pp. 389–419 |
| [2] | J.A. Thas, "Combinatorics of partial geometries and generalized quadrangles" M. Aigner (ed.) , Higher Combinatorics , Reidel (1977) pp. 183–199 |
| [3] | J.A. Thas, "Construction of maximal arcs and partial geometries" Geometrica Dedicata , 3 : 1 (1974) pp. 61–64 |
Comments
For nets see also Net (in finite geometry).
At present there are only two infinite series and a few sporadic examples of partial geometries of type d) known. One of these series is related to maximal arcs in projective planes (cf. [3]) and the other to hyperbolic quadrics in projective spaces of characteristic 2 (cf. [a1]).
There is an important connection to strongly regular graphs: The point graph (which has the points of the partial geometry as vertices, with two points being adjacent if and only if they are collinear in the partial geometry) is a strongly-regular graph, cf. [1]. This allows one to apply the many known existence criteria for such graphs to partial geometries. A good survey on strongly-regular graphs and partial geometries, containing non-existence results and descriptions of the known examples, has been given in [a2]. For the special case of generalized quadrangles, there is now a monograph available, see [a3].
References
| [a1] | F. de Clerck, R.H. Dye, J.A. Thas, "An infinite class of partial geometries associated with the hyperbolic quadric in 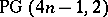 " Europ. J. Comb. , 1 (1980) pp. 323–326 " Europ. J. Comb. , 1 (1980) pp. 323–326 |
| [a2] | A.E. Brouwer, J.H. van Lint, "Strongly regular graphs and partial geometries" D.M. Jackson (ed.) S.A. Vanstone (ed.) , Enumeration and Design , Acad. Press (1984) pp. 85–122 |
| [a3] | S.E. Payne, J.A. Thas, "Finite generalized quadrangles" , Pitman (1985) |
| [a4] | A.E. Brouwer, A.M. Cohen, A. Neumaier, "Distance regular graphs" , Springer (1989) pp. 229 |
| [a5] | L.M. Batten, "Combinatorics of finite geometries" , Cambridge Univ. Press (1986) pp. Chapt. 7 |
| [a6] | J.H. van Lint, "Partial geometries" , Proc. Internat. Congress Mathematicians (Warsawa 1983) , 2 , PWN & North-Holland (1984) pp. 1579–1590 |
Partial geometry. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Partial_geometry&oldid=51405