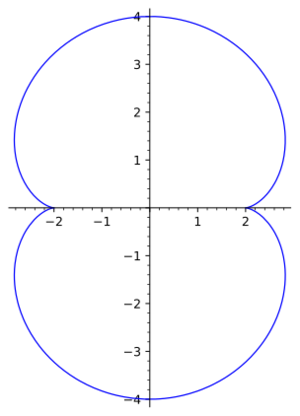
Nephroid
From Encyclopedia of Mathematics
2020 Mathematics Subject Classification: Primary: 52A10 [MSN][ZBL]
An epicycloid with parameter $m=2$; an algebraic plane curve with equation $$ x= 3r \cos\theta-r\cos\left[3\theta\right] \,, $$ $$ y= 3r \sin\theta-r\sin\left[3\theta\right] \ . $$
The nephroid is the catacaustic of the cardioid with respect to a cusp, and of a circle with respect to a point at infinity; the evolute of a nephroid is another nephroid.
The nephroid of Freeth is the strophoid of a circle with respect to its centre and a point on the circumference. It has equation $$ r = a(1 + 2\sin(\theta/2)) \ . $$
References
- J.D. Lawrence, "A catalog of special plane curves" , Dover (1972) ISBN 0-486-60288-5 Zbl 0257.50002
How to Cite This Entry:
Nephroid. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Nephroid&oldid=54470
Nephroid. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Nephroid&oldid=54470