Multivalent function
A notion which is a natural generalization of that of a univalent function. A regular or meromorphic function $ f ( z) $
in a domain $ D $
of the complex $ z $-
plane is called $ p $-
valent in $ D $(
$ p = 1 , 2 ,\dots $)
if in this domain it takes each of its values at most $ p $
times, that is, if the number of roots of the equation $ f ( z) = w $
in $ D $,
for any $ w $,
does not exceed $ p $.
Geometrically this means that above each point of the $ w $-
plane lie at most $ p $
points of the Riemann surface into which $ w = f ( z) $
maps $ D $.
For $ p = 1 $,
$ f ( z) $
is univalent in $ D $.
Alongside this most simple class of $ p $- valent functions, a major role in the theory of multivalent functions is played by functions which are $ p $- valent in a certain generalized sense: "p-valent in the mean" . Let $ f ( z) $ be a regular or meromorphic function in a domain $ D $ of the $ z $- plane, let $ n ( w) $ be the number of roots in $ D $ of the equation $ f ( z) = w $ and let $ p $ be a positive number. The function $ f ( z) $ is called $ p $- valent in the mean over circles in $ D $ if for all $ R > 0 $:
$$ \frac{1}{2 \pi } \int\limits _ { 0 } ^ { {2 } \pi } n ( R e ^ {i \phi } ) \ d \phi \leq p . $$
Geometrically this means that the linear measure of the arc on the Riemann surface to which $ w = f ( z) $ maps $ D $ and projecting to the circle $ | w | = R $ does not exceed $ p $ times the length of this circle. A function $ f ( z) $ is called $ p $- valent in the mean over areas in $ D $ if
$$ \int\limits _ { 0 } ^ { R } \left ( \int\limits _ { 0 } ^ { {2 } \pi } n ( \rho e ^ {i \phi } ) d \phi \right ) \rho d \rho \leq \ p \pi R ^ {2} $$
for all $ R > 0 $. Geometrically this means that the area of a part of the Riemann surface to which $ w = f ( z) $ maps $ D $ and projecting to a disc $ | w | < R $ does not exceed $ p $ times the area of this disc. From these definitions it follows that a function which is $ p $- valent in some domain is also $ p $- valent in the mean over circles in it, and a function which is $ p $- valent in the mean over circles is $ p $- valent in the mean over areas. A function which is $ p $- valent in the mean may turn out to be infinitely-valent.
Multivalent functions, like univalent ones, have been studied in various ways: from the point of view of distortion characteristics of the domain under the mappings by these functions, from estimates on the coefficients of series of representing these functions, etc. They have many extremal properties, similar to the extremal properties of univalent functions. For example, there are the following generalizations to the case of $ p $- valent functions of two classical results in the theory of univalent functions: the area principle and estimates for the second coefficient (see Bieberbach conjecture).
If a function
$$ \tag{1 } F ( \zeta ) = \ \sum _ { m=1} ^ { p } \alpha _ {m} \zeta ^ {m} + \sum _ { n=0} ^ \infty \frac{a _ {n} }{\zeta ^ {n} } ,\ \ \alpha _ {p} \neq 0 ,\ \ | \zeta | > 1 , $$
is $ p $- valent and regular in the domain $ | \zeta | > 1 $, except for a pole at $ \zeta = \infty $, then
$$ \tag{2 } \sum _ { n=1} ^ \infty n | a _ {n} | ^ {2} \leq \ \sum _ { m=1} ^ { p } m | \alpha _ {m} | ^ {2} . $$
If a function
$$ \tag{3 } f ( z) = z ^ {p} + a _ {p+} 1 z ^ {p+} 1 + \dots $$
is regular and $ p $- valent in the disc $ | z | < 1 $, then
$$ \tag{4 } | a _ {p+} 1 | \leq 2 p . $$
Inequalities (2) and (4) are best possible. These two results are related to the earliest fundamental results in the theory of $ p $- valent functions. Inequality (2) has also been proved for functions of the form (1) that are $ p $- valent in the mean over areas in $ | \zeta | > 1 $, and (4) has been proved for functions of the form (3) that are $ p $- valent in the mean over areas in $ | z | < 1 $.
Research into the class of $ p $- valent functions was significantly advanced by the possibility of considering it as a subclass of the functions that are $ p $- valent in the mean. Precise analogues of the basic distortion and covering theorems for univalent functions have also been obtained for $ p $- valent functions (see Distortion theorems; Covering theorems). Namely: For a function $ f ( z) $ of the form (3) that is $ p $- valent in the mean over circles in the disc $ | z | < 1 $, one has the sharp estimates:
$$ \frac{| z | ^ {p} }{( 1 + | z | ) ^ {2p} } \leq \ | f ( z) | \leq \ \frac{| z | ^ {p} }{( 1 - | z | ) ^ {2p} } , $$
$$ | f ^ { \prime } ( z) | < p | z | ^ {p-} 1 \cdot \frac{1 + | z | }{( 1 - | z | ) ^ {2p+} 1 } ,\ | z | < 1 ; $$
the function $ f ( z) $ takes, in $ | z | < 1 $, each value $ w $ with $ | w | < 1 / 4 ^ {p} $ exactly $ p $ times (a direct analogue of the Koebe covering theorem, cf. Koebe theorem). This latter property also holds for functions $ f ( z) $ of the form (3) that are $ p $- valent in the mean over areas in $ | z | < 1 $. For functions that are $ p $- valent in the mean over circles there are a number of best possible results characterizing the growth of their coefficients. Thus, for functions of the form
$$ \tag{5 } f ( z) = \ \sum _ { n=0} ^ \infty a _ {n} z ^ {n} $$
that are $ p $- valent in the mean over circles in $ | z | < 1 $, $ p > 0 $, the limit
$$ \alpha = \ \lim\limits _ {r \rightarrow 1 - 0 } \ ( 1 - r ) ^ {2p} \ \max _ {| z| = r } \ | f ( z) | $$
exists and is, moreover, finite, and
$$ \lim\limits _ {n \rightarrow \infty } \ \frac{| a _ {n} | }{n ^ {2p-} 1 } = \ \frac \alpha {\Gamma ( 2 p ) } $$
for $ p > 1 / 4 $. Whenever an estimate for $ \alpha $ is obtained, a corresponding sharp estimate for the asymptotic growth of the coefficients follows. In particular, if $ f ( z) $ has the form (3), then the latter equality takes the form
$$ \lim\limits _ {n \rightarrow \infty } \ \frac{| a _ {n} | }{n ^ {2p-} 1 } = \ \frac \alpha {( 2 p - 1 ) ! } , $$
where $ \alpha < 1 $, except for the case when $ f ( z) = z ^ {p} ( 1 - z e ^ {i \theta } ) ^ {-} 2p $( $ \theta $ real). Furthermore, for functions of the form (3) that are $ p $- valent in the mean over circles in $ | z | < 1 $, one has the sharp estimate
$$ | a _ {p+} 2 | \leq p ( 2 p + 1 ) , $$
while for the subclass of $ p $- valent functions of this form there is a sharp estimate for the following coefficient:
$$ | a _ {p+} 3 | \leq \ \frac{2}{3} p ( p + 1 ) ( 2 p + 1 ) . $$
The two latter inequalities are, for multivalent functions, the analogues of the estimates $ | a _ {3} | \leq 3 $ and $ | a _ {4} | \leq 4 $, known for univalent functions (see Bieberbach conjecture). Since the extremal functions in the above turn out to be $ p $- valent functions, all of these results are best possible even in the class of $ p $- valent functions.
For functions of the form (5) that are $ p $- valent in the mean over areas in the disc $ | z | < 1 $, the following estimates for their coefficients are known to hold for all $ n \geq 1 $:
$$ \tag{6 } | a _ {n} | < A ( p) \mu _ {p} n ^ {2p-} 1 \ \ ( p > 1 / 4 ) , $$
$$ \tag{7 } | a _ {n} | < A | a _ {0} | n ^ {-} 1/2 \mathop{\rm log} ( n + 1 ) \ ( p = 1 / 4 ) , $$
$$ \tag{8 } | a _ {n} | < A ( p) | a _ {0} | \left [ \frac{ \mathop{\rm log} ( n + 1 ) }{n } \right ] ^ {1/2} \ ( 0 < p < 1 / 4 ) , $$
$$ \tag{9 } | | a _ {n+} 1 | - | a _ {n} | | < A ( p) \mu _ {p} n ^ {2p-} 2 \ ( p \geq 1 ) , $$
as well as the estimate
$$ \tag{10 } \max _ {| z| = r } \ | f ( z) | < A ( p) \mu _ {p} ( 1 - r ) ^ {-} 2p \ \ ( 0 < r < 1 ) ; $$
here $ A ( p) $ depends only on $ p $ and $ \mu _ {p} = \max _ {0 \leq \nu \leq p } | a _ \nu | $. The order of the quantities in (6), (9) and (10) is best possible.
There is also the following analogue for multivalent functions of a theorem known for univalent meromorphic functions: In the class of all functions
$$ F ( \zeta ) = \zeta ^ {p} \left ( 1 + \frac{a _ {1} } \zeta + \dots \right ) $$
that are $ p $- valent and regular in $ | \zeta | > 1 $, except for a pole at $ \zeta = \infty $, and have at a fixed point $ \zeta _ {0} \neq \infty $ of this domain the expansion
$$ F ( \zeta ) = F ( \zeta _ {0} ) + \frac{F ^ { ( p) } ( \zeta _ {0} ) }{p ! } ( \zeta - \zeta _ {0} ) ^ {p} + \dots , $$
the range of values of the functional
$$ w = \mathop{\rm log} \ \frac{F ^ { ( p) } ( \zeta _ {0} ) }{p ! } $$
is the disc
$$ | w | \leq - p \ \mathop{\rm log} \left ( 1 - \frac{1}{| \zeta _ {0} | ^ {2} } \right ) . $$
Apart from the above-mentioned fundamental classes of multivalent functions, a significant place in the investigations is held by special classes of multivalent functions, for example, functions which are typically real of order $ p $, $ p $- valent star-like, $ p $- valent convex, $ p $- valent close-to-convex, $ p $- valent bounded, and others, which are generalizations of, respectively, typically-real, star-like, convex, close-to-convex, bounded univalent, and other functions (cf. Typically-real function; Star-like function; Convex function (of a complex variable)). A function
$$ \tag{11 } f ( z) = \ \sum _ { n=1} ^ \infty a _ {n} z ^ {n} $$
is called typically real of order $ p $ in $ | z | < 1 $ if it is regular, has real coefficients $ a _ {n} $ and if there is a number $ \delta = \delta ( f ) $, $ 0 < \delta < 1 $, such that for each $ r $ in the interval $ 1 - \delta < r < 1 $ the imaginary part $ \mathop{\rm Im} \{ f ( z) \} $ changes its sign on the circle $ | z | = r $ exactly $ 2p $ times. Here $ f ( z) $ may be more than $ p $- valent in $ | z | < 1 $. For its coefficients one has the sharp estimates:
$$ \tag{12 } | a _ {n} | \leq \ \sum _ { k=1} ^ { p } \frac{2 k ( n + p ) ! }{( n ^ {2} - k ^ {2} ) ( p - k ) ! ( p + k ) ! ( n - p - 1 ) ! } | a _ {k} | ,\ $$
$$ n > p. $$
One of the analogues of the Bieberbach conjecture for functions of the form (11) that are regular and $ p $- valent in $ | z | < 1 $ is Goodman's conjecture on the validity of (12) for the coefficients $ a _ {n} $. In particular, Goodman's conjecture holds for $ p $- valent typically-real functions of order $ p $ in $ | z | < 1 $. It has also been proved to hold for a class of $ p $- valent functions which is a generalization of the class of univalent functions that are convex in the direction of the imaginary axis. Another analogue of the Bieberbach conjecture for $ p $- valent functions is the following conjecture of Goodman. Let a function
$$ f ( z) = z ^ {q} + \sum _{n=q+1} ^ \infty a _ {n} z ^ {n} ,\ \ q \geq 1 , $$
be regular and $ p $- valent, $ p = 1 , 2 \dots $ in $ | z | < 1 $, and let it have $ t $ zeros $ \alpha _ {1} \dots \alpha _ {t} $ in $ 0 < | z | < 1 $, $ t \leq p - q $. The conjecture is that $ | a _ {n} | \leq B _ {n} $, $ n> q $, where $ B _ {n} $ is the $ n $- th coefficient in the expansion
$$ \frac{z ^ {q} }{( 1 - z ) ^ {2q} } \left ( \frac{1 + z }{1 - z } \right ) ^ {2 ( p - q - t ) } \frac{1}{( 1 - z ) ^ {2t} } \times $$
$$ \times \prod _ {j=1} ^ { t } \left ( 1 + \frac{z}{| \alpha _ {j} | } \right ) ( 1 + | \alpha _ {j} | z ) \equiv $$
$$ \equiv \ z ^ {q} + \sum _{n=q+1} ^ \infty B _ {n} z ^ {n} ,\ | z | < 1 . $$
For typically-real functions of order $ p $ in $ | z | < 1 $ this inequality has been proved.
The classes of $ p $- valent star-like and $ p $- valent convex functions, $ S ( p) $ and $ C ( p) $ respectively, are defined as follows. A function $ f ( z) $ belongs to $ S ( p) $, $ p = 1 , 2 \dots $ if it is regular in $ | z | < 1 $, if $ f ( 0) = 0 $ and if there is a number $ \rho $, $ 0 < \rho < 1 $, such that
$$ \mathop{\rm Re} \left \{ \frac{z f ^ { \prime } ( z) }{f ( z) } \right \} > 0 , $$
$$ \int\limits _ { 0 } ^ { {2 } \pi } \mathop{\rm Re} \left \{ \frac{z f ^ { \prime } ( z) }{f ( z) } \right \} d \theta = 2 p \pi ,\ \theta = \mathop{\rm arg} z , $$
for $ \rho < | z | < 1 $. A function $ f ( z) $ belongs to $ C ( p) $, $ p = 1 , 2 \dots $ if it is regular in $ | z | < 1 $, if $ f ( 0) = 0 $ and if there is a $ \rho $ such that
$$ 1 + \mathop{\rm Re} \left \{ \frac{z f ^ { \prime\prime } ( z) }{f ^ { \prime } ( z) } \right \} > 0 , $$
$$ \int\limits _ { 0 } ^ { {2 } \pi } \left [ 1 + \mathop{\rm Re} \left \{ \frac{z f ^ { \prime\prime } ( z) }{f ^ { \prime } ( z) } \right \} \right ] d \theta = 2 p \pi ,\ \theta = \mathop{\rm arg} z , $$
for $ \rho < | z | < 1 $. A number of sharp estimates has been obtained for functions of these two classes.
The classes $ S ( p) $ and $ C ( p) $ turn out to be subclasses of a wider class of $ p $- valent functions: the class of $ p $- valent close-to-convex functions. A function
$$ F ( z) = \ \sum _ {n=1} ^ \infty a _ {n} z ^ {n} $$
that is regular in $ | z | < 1 $ is called $ p $- valent close-to-convex if it satisfies one of the following conditions:
A) there is a function $ f ( z) \in S ( p) $ and a number $ \rho $, $ 0 < \rho < 1 $, such that
$$ \tag{13 } \mathop{\rm Re} \left \{ \frac{z F ^ { \prime } ( z) }{f ( z) } \right \} > 0 \ \ ( \rho < | z | < 1 ) ; $$
B) $ F ( z) $ is regular on $ | z | = 1 $ and there is a function $ f ( z) \in S ( p) $, also regular on $ | z | = 1 $, such that (13) is satisfied on $ | z | = 1 $.
For functions $ F ( z) $ of this class sharp upper and lower bounds for $ | F ^ { \prime } ( z) | $ have been found and (12) has been proved: for $ n = p + 1 $ for all functions of this class, and for $ n \geq p + 1 $ for the functions in this class with real coefficients. Sharp estimates generalizing certain results for bounded univalent functions have been obtained for bounded functions that are $ p $- valent in the corresponding generalized sense. Thus, the radius of $ p $- valency has been found in the class of functions regular and bounded in a disc: If $ f ( z) $ is regular and bounded in modulus by one in the disc $ | z | < 1 $ and normalized by the conditions $ f ( 0) = 0 $, $ f ^ { \prime } ( 0) = a _ {1} $, $ 0 < | a _ {1} | < 1 $, then the radius $ \rho $ of the largest disc $ | z | < \rho $ in which it is $ p $- valent is given by the equation
$$ \frac{( p + 1 ) \rho ^ {p} ( 1 - \rho ^ {2} ) }{1 - \rho ^ {2p+} 2 } = \ | a _ {1} | ,\ \ 0 < \rho < 1 . $$
This theorem generalizes, to the case $ p > 1 $, Landau's theorem on the radius of univalency of functions that are regular and bounded in the disc $ | z | < 1 $.
Various sufficient conditions are known for a function that is regular in a domain to be $ p $- valent in it. For example, if $ f ( z) $ is regular in a convex domain $ D $ and if there are a real number $ \theta $ and an integer $ k $, $ 0 \leq k \leq p - 1 $, such that
$$ \mathop{\rm Re} \left \{ e ^ {i \theta } \frac{d ^ {p} }{d z ^ {p} } [ z ^ {k} f ( z) ] \right \} > 0 ,\ \ z \in D , $$
then $ f ( z) $ is $ p $- valent in $ D $.
Multivalent functions have also been studied in multiply-connected domains. In this case many estimates can be expressed in terms of functions mapping the given multiply-connected domain into a canonical Riemann surface, and in terms of the Bergman kernel function. The first basic result related to the question of the existence of conformal mappings of a multiply-connected domain onto a multi-sheeted canonical surface is the following theorem of Grunsky: Let $ D $ be a finitely-connected domain in the $ z $- plane with $ z = \infty $ as an interior point and with boundary components which are not points, and let $ Q _ {p} ( z) $ be a given polynomial of degree $ p \geq 1 $; then for any given $ \theta $, $ 0 \leq \theta < \pi $, there is a unique function $ \Phi _ \theta ( z) $, regular in $ D $ except for a pole at $ z = \infty $, whose principal part at $ z = \infty $( including the free term) coincides with $ Q _ {p} ( z) $ and which associates with each boundary component of $ D $ a rectilinear segment of slope $ \theta $ with the real axis. In other words, the function $ w = \Phi _ \theta ( z) $ maps $ D $ into the whole $ p $- sheeted $ w $- plane with parallel slits of slope $ \theta $. The existence of conformal mappings of a given finitely-connected domain onto other canonical multi-sheeted surfaces has also been proved; extremal properties similar to certain extremal properties of univalent functions have been established for multivalent functions. It has been shown that the most general class of multivalent functions, meromorphic in a finitely-connected domain, for which the area theorem holds has a simple geometric characterization.
The basic methods of research of multivalent functions are the method of boundary integration, the symmetrization method and the method of quadratic differentials (cf. Quadratic differential).
Variational methods in the theory of multivalent functions are less effective than in the theory of univalent functions.
References
| [1] | G.M. Goluzin, "On $p$-valent functions" Mat. Sb. , 8 : 2 (1940) pp. 277–283 (In Russian) (German abstract) |
| [2] | W.K. Hayman, "Multivalent functions" , Cambridge Univ. Press (1958) |
| [3] | J.A. Jenkins, "Univalent functions and conformal mapping" , Springer (1958) |
| [4] | K. Pethe, "Estimation du coefficient 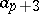 de la fonction $p$-valente dans le cercle unité" Bull. Acad. Polon. Sci. , 20 : 3 (1972) pp. 219–220 (Russian and English abstracts) de la fonction $p$-valente dans le cercle unité" Bull. Acad. Polon. Sci. , 20 : 3 (1972) pp. 219–220 (Russian and English abstracts) |
| [5] | A.E. Livingston, "$p$-valent close-to-convex functions" Trans. Amer. Math. Soc. , 115 : 3 (1965) pp. 161–179 |
| [6] | R.J. Leach, "Coefficient estimates for certain multivalent functions" Pacific J. Math. , 74 : 1 (1978) pp. 133–142 |
| [7a] | J. Krzyz, "On the derivative of bounded $p$-valent functions" Ann. Univ. Mariae Curie-Sklodowska Sect. A , 12 : 2 (1958) pp. 23–28 (Russian and Polish abstracts) |
| [7b] | J. Krzyz, "Distortion theorems for bounded $p$>-valent functions" Ann. Univ. Mariae Curie-Sklodowska Sect. A , 12 : 3 (1958) pp. 29–38 (English and Polish abstracts) |
| [8] | S. Ozaki, Sci. Rep. Tokyo Bunrika Daigaku A , 2 : 40 (1935) pp. 167–188 |
| [9] | Yu.E. Alenitsyn, "Area theorems for functions analytic in a finitely connected domain" Math. USSR Izv. , 7 : 5 (1973) pp. 1129–1151 Izv. Akad. Nauk SSSR Ser. Mat. , 37 : 5 (1973) pp. 1132–1154 |
| [10] | S.K. Singh, Math. Student , 30 : 1–2 (1973) pp. 79–90 |
| [11] | A.W. Goodman, "Open problems on univalent and multivalent functions" Bull. Amer. Math. Soc. , 74 : 6 (1968) pp. 1035–1050 |
Multivalent function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Multivalent_function&oldid=54912