Massive Thirring model
A relativistic quantum field theory in one space and one time dimension [a11]. It is defined in terms of a two-component quantized fermion field $ \Psi _ {k} ( x,t ) $(
$ k = 1,2 $)
obeying the equal-time anti-commutation relations (cf. Commutation and anti-commutation relationships, representation of)
$$ \{ \Psi _ {k} ( x,t ) , \Psi _ {m} ^ * ( y,t ) \} = \delta _ {km } \delta ( x - y ) ; $$
$$ \{ \Psi _ {k} ( x,t ) , \Psi _ {m} ( y,t ) \} = \{ \Psi _ {k} ^ * ( x,t ) , \Psi _ {m} ^ * ( y,t ) \} = 0. $$
Here $ ^ * $ denotes Hermitian conjugation, $ \delta _ {kl } $ is the Kronecker delta and $ \delta ( x - y ) $ is the Dirac delta-function. The Lagrangian of the model is
$$ L = \int\limits dx \left [ i {\overline \Psi \; } \gamma ^ \mu \partial _ \mu \Psi - m _ {0} {\overline \Psi \; } \Psi - { \frac{g}{2} } : [ {\overline \Psi \; } \gamma _ \mu \Psi ] ^ {2} : \right ] , $$
where
$$ \gamma _ {0} = \left ( \begin{array}{cc} 0 & 1 \\ 1 & 0 \\ \end{array} \right ) , \gamma _ {1} = \left ( \begin{array}{cc} 0 & 1 \\ - 1 & 0 \\ \end{array} \right ) , {\overline \Psi \; } = \Psi ^ * \gamma ^ {0} , $$
$ m _ {0} $ is the bare fermion mass and $ g $ is the bare coupling constant. Colons denote normal ordering, which means that $ \Psi $ stands to the right and $ \Psi ^ * $ to the left. Due to ultraviolet divergences, mass renormalization is necessary to obtain finite expressions for physical quantities.
The massive Thirring model is integrable and can be solved by the Bethe Ansatz method [a1], [a2], [a3].
In the region $ 0 < g < \pi $, the spectrum of low-lying excitations is described in terms of an elementary fermion, its anti-particle and their bound states. All dispersion relations are of the relativistic form $ E ^ {2} = m ^ {2} + p ^ {2} $, where $ p $ is the momentum and $ m $ is the mass of the particle considered. If one denotes the (renormalized) fermion mass by $ M $, the bound state masses are given by
$$ M _ {n} = 2 M \sin \left ( { \frac{\pi ( \pi - g ) }{2 ( \pi + g ) } } n \right ) , n = 1 \dots \left [ { \frac{2 \pi }{\pi - \gamma } } \right ] - 1. $$
Here, $ [ x ] $ denotes the largest integer smaller than or equal to $ x $. The fermion-antifermion scattering matrix for a state with definite parity (symmetrized or anti-symmetrized wave function) is given by ([a4], [a5], [a2]):
$$ S _ \pm ( \theta ) = u _ \pm ( \theta ) S ( \theta ) , $$
$$ S ( \theta ) = $$
$$ = { \mathop{\rm exp} } \left ( - \int\limits _ { 0 } ^ \infty { \frac{dx }{x} } { \frac{ \sinh ( 2i \theta x/ \gamma ) \sinh ( x ( \pi - \gamma ) / \gamma ) }{ \sinh ( x ) \cosh ( \pi x/ \gamma ) } } \right ) , $$
$$ \left \{ \begin{array}{l} {u _ {+} ( \theta ) = { \frac{ \sinh ( \pi ( i \pi + \theta ) /2 \gamma ) }{ \sinh ( \pi ( i \pi - \theta ) /2 \gamma ) } } , \ } \\ {u _ {-} ( \theta ) = - { \frac{ \cosh ( \pi ( i \pi + \theta ) /2 \gamma ) }{ \cosh ( \pi ( i \pi - \theta ) /2 \gamma ) } } , \ } \end{array} \right . $$
where
$$ \gamma = \pi { \frac{\pi - g }{\pi + g } } $$
and $ \theta = \beta _ {1} - \beta _ {2} $ is the rapidity difference of the scattering particles. The rapidity variable is related to the momentum by the relation $ p = M \sinh \beta $. The poles in $ S _ \pm ( \theta ) $ correspond to the fermion-antifermion bound states mentioned above. The bound state scattering matrices are obtained from $ S _ \pm ( \theta ) $ by taking the residues at the poles. The multi-particle scattering matrices factorize into products of two-particle ones. Due to the infinite number of (quantum) integrals of motion there is no particle production.
The massive Thirring model is equivalent to the quantum sine-Gordon model in the sector of zero topological charge [a6], [a7]. The fermion in the massive Thirring model corresponds to the soliton in this sine-Gordon model. Correspondingly, the soliton-antisoliton scattering matrix in the sine-Gordon model is given by $ S _ \pm ( \theta ) $. The ultraviolet divergences in the massive Thirring model can be regularized by putting the model on a lattice. One such lattice regularization is given by the XYZ Heisenberg spin chain, [a8].
In the repulsive region $ - \pi < g < 0 $, the massive Thirring model can also be solved by the Bethe Ansatz method. However different ways of regularizing the theory lead to different answers for the spectrum and scattering matrices [a12], [a8], [a9].
Recently (1992), form-factors for the massive Thirring model have been computed in [a10].
References
| [a1] | H. Bergknoff, H. Thacker, "Structure and solution of the massive Thirring model" Phys. Rev. , D19 (1979) pp. 3666 |
| [a2] | V.E. Korepin, "Direct calculation of the $S$-matrix in the massive Thirring model" Theor. Math. Phys. , 41 (1979) pp. 169 |
| [a3] | V.E. Korepin, N.M. Bogoliubov, A.G. Izergin, "Quantum inverse scattering method, correlation functions and algebraic Bethe Ansatz" , Cambridge Univ. Press (1993) |
| [a4] | A.B. Zamolodchikov, "Exact two-particle 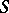 -matrix of quantum solitons of the sine-Gordon model" Soviet Phys. JETP Lett. , 25 (1977) pp. 468 -matrix of quantum solitons of the sine-Gordon model" Soviet Phys. JETP Lett. , 25 (1977) pp. 468 |
| [a5] | M. Karowski, H.-J. Thun, T.T. Truong, P.H. Weisz, "On the uniqueness of a purely elastic 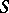 -matrix in -matrix in 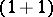 dimensions" Phys. Lett. , 67B (1977) pp. 321 dimensions" Phys. Lett. , 67B (1977) pp. 321 |
| [a6] | S. Coleman, "Quantum sine-Gordon equation as the massive Thirring model" Phys. Rev. , D11 (1975) pp. 2088 |
| [a7] | S. Mandelstam, "Soliton operators for the quantized sine-Gordon equation" Phys. Rev. , D11 (1975) pp. 3026 |
| [a8] | A. Luther, "Eigenvalue spectrum of interacting massive Fermions in one dimension" Phys. Rev. , B14 (1976) pp. 2153 |
| [a9] | V.E. Korepin, "The mass spectrum and the 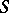 -matrix of the massive Thirring model in the repulsive case" Comm. Math. Phys. , 76 (1980) pp. 165 -matrix of the massive Thirring model in the repulsive case" Comm. Math. Phys. , 76 (1980) pp. 165 |
| [a10] | F.A. Smirnov, "Form factors in completely integrable models of quantum field theory" , World Sci. (1992) |
| [a11] | W. Thirring, "A solvable relativistic field theory" Ann. of Phys. , 3 (1958) pp. 91 |
| [a12] | G.I. Japaridze, A.A. Nersesyan, P.B. Wiegmann, "Exact results in the two-dimensional 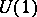 -symmetric Thirring model" Nucl. Phys. , B230 (1984) pp. 511 -symmetric Thirring model" Nucl. Phys. , B230 (1984) pp. 511 |
Massive Thirring model. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Massive_Thirring_model&oldid=55769