Kodaira theorem

Kodaira's vanishing theorem

A theorem on the vanishing of the cohomology groups $ H ^ {i} ( X, {\mathcal O} ( L) ) $, $ i < \mathop{\rm dim} X $, where $ {\mathcal O} ( L) $ is the sheaf of holomorphic sections of the negative vector bundle $ L $ of rank $ 1 $ on a compact complex manifold $ X $. An equivalent statement of Kodaira's vanishing theorem is that

$$ H ^ {i} ( X, {\mathcal O} ( L \otimes K _ {X} ) ) = 0 ,\ \ i > 0 , $$

for any positive vector bundle of rank 1 (here $ K _ {X} $ denotes the canonical line bundle on $ X $). In terms of divisors (cf. Divisor) Kodaira's vanishing theorem is stated as the equation $ H ^ {i} ( X , {\mathcal O} _ {X} ( - D ) ) = 0 $ for $ i < \mathop{\rm dim} X $ and any divisor $ D $ such that for some $ n \geq 1 $, $ n D $ is a hyperplane section in some projective imbedding of $ X $.

The theorem was proved by transcendental methods by K. Kodaira [1] (see also [2]) as a generalization to arbitrary dimension of the classical theorem on the regularity of an adjoint system on an algebraic surface. There exists an example of a normal algebraic surface over a field of positive characteristic for which Kodaira's vanishing theorem is false [4].

Kodaira's theorem also holds for holomorphic vector bundles of arbitrary rank that are negative in the sense of J. Nakano. The following result is also a generalization of Kodaira's theorem:

$$ H ^ {i} ( X , \Omega ^ {p} ( L) ) = 0 \ \ \textrm{ for } \ p + i \geq \mathop{\rm dim} X + r , $$

where $ L $ is a weakly-positive vector bundle of rank $ r $ on the compact complex manifold $ X $, and $ \Omega ^ {p} ( L) = \Omega ^ {p} \otimes {\mathcal O} ( L) $ is the sheaf of holomorphic forms (cf. Holomorphic form) of degree $ p $ with values in $ L $. For weakly-negative vector bundles $ L $, vanishing takes place when $ p + i \leq \mathop{\rm dim} X - r $. Analogues of these theorems have been obtained for weakly-complete manifolds $ X $, that is, manifolds admitting a smooth pluriharmonic function $ \psi $ such that the set $ \{ {x \in X } : {\psi ( x) < c } \} $ is relatively compact in $ X $ for all $ c \in \mathbf R $, and for compact complex spaces $ X $ having $ n = \mathop{\rm dim} X $ algebraically-independent meromorphic functions [5].

References

[1]	K. Kodaira, "On a differential geometric method in the theory of analytic stacks" Proc. Nat. Acad. Sci. USA , 39 (1953) pp. 1268–1273 MR0066693 Zbl 0053.11701
[2]	R.O. Wells jr., "Differential analysis on complex manifolds" , Springer (1980) MR0608414 Zbl 0435.32004
[3]	D. Mumford, "Pathologies III" Amer. J. Math. , 89 : 1 (1967) pp. 94–104 MR0217091 Zbl 0146.42403
[4]	O. Zariski, "Algebraic surfaces" , Springer (1971) MR0469915 Zbl 0219.14020
[5]	A.L. Onishchik, "Pseudoconvexity in the theory of complex spaces" J. Soviet Math. , 14 : 4 (1980) pp. 1363–1407 Itogi Nauk. Algebra Topol. Geom. , 15 (1977) pp. 93–171 Zbl 0449.32020

Comments

Counterexamples to Kodaira's theorem for non-singular varieties over a field of positive characteristic were given by M. Raynaud [a1]. There exists a much stronger version of Kodaira's theorem, due to E. Viehweg and Y. Kawamata [a2].

Recently, many generalizations of Kodaira vanishing have been found, see [a3].

References

[a1]	M. Raynaud, "Contre-example du "vanishing theorem" en caractéristique 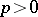" K.G. Ramanathan (ed.) , C.P. Ramanujam, a tribute , Springer (1978) pp. 273–278
[a2]	E. Viehweg, "Vanishing theorems and positivity in algebraic fibre spaces" , Proc. Internat. Congress Mathematicians (Berkeley, 1986) , 1 , Amer. Math. Soc. (1987) pp. 682–688 MR0934270 Zbl 0685.14013
[a3]	J. Kollar, "Vanishing theorems for cohomology groups" S.J. Bloch (ed.) , Algebraic geometry (Bowdoin, 1985) , Proc. Symp. Pure Math. , 46 : 2 , Amer. Math. Soc. (1987) pp. 233–243 MR0927959 Zbl 0658.14012