Pluriharmonic function
A function $ u = u( z) $
of $ n $
complex variables $ z = ( z _ {1} \dots z _ {n} ) $
in a domain $ D $
of the complex space $ \mathbf C ^ {n} $,
$ n \geq 1 $,
that has continuous derivatives with respect to the coordinates $ x _ \nu , y _ \nu $,
$ z _ \nu = x _ \nu + iy _ \nu $,
$ \nu = 1 \dots n $,
in $ D $
up to the second order inclusive and that satisfies the following system of $ n ^ {2} $
equations in $ D $:
$$ \tag{1 } \left . \begin{array}{c} \frac{\partial ^ {2} u }{\partial x _ \mu \partial x _ \nu } + \frac{\partial ^ {2} u }{\partial y _ \mu \partial y _ \nu } = 0, \\ \frac{\partial ^ {2} u }{\partial x _ \mu \partial y _ \nu } - \frac{\partial ^ {2} u }{\partial y _ \mu \partial x _ \nu } = 0, \end{array} \right \} $$
$$ \mu , \nu = 1 \dots n. $$
One uses the formal derivatives
$$ \frac{\partial u }{\partial z _ \nu } = \frac{1}{2} \left ( \frac{\partial u }{ \partial x _ \nu } - i \frac{\partial u }{\partial y _ \nu } \right ) ,\ \ \frac{\partial u }{\partial \overline{z}\; _ \nu } = \frac{1}{2} \left ( \frac{\partial u }{\partial x _ \nu } + i \frac{\partial u }{\partial y _ \nu } \right ) $$
to write (1) in the more compact form:
$$ \tag{2 } \frac{\partial ^ {2} u }{\partial \overline{z}\; _ \mu \partial z _ \nu } = 0,\ \ \mu , \nu = 1 \dots n. $$
The significance of the class of pluriharmonic functions is determined by the fact that the real and imaginary parts $ u = \mathop{\rm Re} f $ and $ v = \mathop{\rm Im} f $ of any holomorphic function $ f = u + iv $ in $ D $ are pluriharmonic functions in $ D $; two such real-valued pluriharmonic functions are called conjugate. Conversely, if one is given a pluriharmonic function $ u $ in a simply-connected neighbourhood $ V $ of a point $ z ^ {0} = x ^ {0} + iy ^ {0} \in \mathbf C ^ {n} $, then there exists a holomorphic function $ f = u + iv $ in $ V $ with real part equal to $ u $. The task of determining this holomorphic function $ f $ amounts to finding the conjugate pluriharmonic function $ v $ from the formula
$$ v( z) = \int\limits _ {z ^ {0} } ^ { z } \ \sum _ {\nu = 1 } ^ { n } \left ( - \frac{\partial u }{\partial y _ \nu } dx _ \nu + \frac{\partial u }{\partial x _ \nu } dy _ \nu \right ) + C,\ \ z \in V, $$
where the integral is independent of the path by virtue of (1).
In general, one may also consider complex-valued pluriharmonic functions, which are defined as solutions to (1) or (2). For $ n > 1 $, the pluriharmonic functions constitute a proper subclass of the class of multiharmonic functions (cf. Multiharmonic function), which in turn is a proper subclass of the class of harmonic functions (cf. Harmonic function); all three classes coincide for $ n= 1 $. On the other hand, the real-valued pluriharmonic functions constitute a proper subclass of the class of plurisubharmonic functions (cf. Plurisubharmonic function) for $ n \geq 1 $, which in turn for $ n > 1 $ is a proper subclass of the class of subharmonic functions (cf. Subharmonic function).
Pluriharmonic functions for $ n > 1 $ have not only the general properties of harmonic functions, but also characteristic ones due, in general, to the fact that (1), or (2), is an overdetermined system in that case. Suppose, for example, that the pluriharmonic function $ u( z) $ in the unit polydisc
$$ U ^ {n} = \{ {z \in \mathbf C ^ {n} } : {| z _ \nu | < 1 ,\ \nu = 1 \dots n } \} $$
is continuous in the closed polydisc $ \overline{ {U }}\; {} ^ {n} $, $ n > 1 $. Then even its boundary values on the skeleton $ T ^ {n} = \{ {\zeta \in \mathbf C ^ {n} } : {| \zeta _ \nu | = 1, \nu = 1 \dots n } \} $, this being a proper part of the entire boundary $ \partial U ^ {n} $, cannot be specified as an arbitrary continuous function $ U ^ {*} ( \zeta ) $, $ \zeta \in T ^ {n} $; they must satisfy certain additional conditions. Therefore, within the class of pluriharmonic functions the Dirichlet problem with data on the skeleton is solvable only for special choices of the boundary data [3].
References
| [1] | B.V. Shabat, "Introduction of complex analysis" , 2 , Moscow (1976) (In Russian) |
| [2] | E.D. Solomentsev, "Harmonic and subharmonic functions and their generalizations" Itogi Nauk. Mat. Anal. Teor. Veroyatnost. Regulirovanie (1964) pp. 83–100 (In Russian) |
| [3] | W. Rudin, "Function theory in polydiscs" , Benjamin (1969) |
Comments
The Dirichlet problem for pluriharmonic functions with data on the unit sphere in $ \mathbf C ^ {n} $ is, of course, also solvable for special data only. The boundary data have to satisfy a certain system of third-order (!) partial differential equations, comparable to the tangential Cauchy–Riemann equations, see [a1], Chapt. 18.
Pluriharmonic functions often serve as a replacement for harmonic functions in the setting of several complex variables. One example is an analogue of classical Hardy spaces (cf. Hardy classes) on the unit disc $ \Delta $. Lumer's Hardy space $ LH ^ {p} $ on $ \Delta $ consists of those holomorphic functions $ f $ such that $ | f | \leq U $ for some plurisubharmonic function $ U $ on $ \Delta $.
References
| [a1] | W. Rudin, "Function theory in the unit ball in 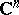 " , Springer (1980) " , Springer (1980) |
Pluriharmonic function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Pluriharmonic_function&oldid=48191