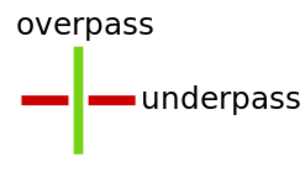Knot and link diagrams

Graphic representations of knots and links, which basically consist of plane projections. Let $ k \subset \mathbf R ^ {3} $ be a link and let $ \pi : \mathbf R ^ {3} \rightarrow \mathbf R ^ {2} \subset \mathbf R ^ {3} $ be the projection $ \pi ( x , y , z ) = \pi ( x , y , 0 ) $. The order of a point $ p \in \pi ( k) $ is defined as the number of elements in the set $ \pi ^ {-1} ( p) \cap k $. A point of order two is called a double point and a point of a order $ > 1 $ a multiple point. One says that a polygonal link $ k $ is situated in regular position if: 1) all its multiple points are double and their number is finite; and 2) no double point is the image of a vertex. Every link may be transformed into regular position by an arbitrarily small rotation of space. If $ k $ is in regular position, then for each double point the branch lying above it (in the direction of the $ z $- axis) is called an overpass and the branch lying below it an underpass. In order to give a diagram of a link in regular position, it is necessary to give its projection $ \pi ( k) \subset \mathbf R ^ {2} $ and cut the image of an underpass at double points (cf. Fig. a).

If the link is oriented, i.e. a manner for traversing each component is given, one indicates this by arrows in the diagram $ D $. If for this traversal of every component of a link the overpasses and underpasses in its projections alternate, the diagram is called alternating. A link having at least one alternating diagram is called an alternating link (cf. Alternating knots and links).

Every domain $ f _ {i} $ into which the projection of a link divides the plane $ \mathbf R ^ {2} $ has a corresponding index $ \nu ( f _ {i} ) $, equal to the sum of the number of circuits accomplished by the projection of each component of the link about an interior point of $ f _ {i} $. By transition to an adjacent domain the index changes by 1, which implies that every domain $ f _ {i} $ may be coloured black or white like a chess board.

In the set of all diagrams in the plane an equivalence relation may be introduced, where two diagrams are called equivalent if and only if the links corresponding to them are isotopic (cf. Isotopy). This makes it possible to reduce the study of knots to plane topology. Thus $ D _ {1} \sim D _ {2} $ if $ D _ {1} $ may be obtained from $ D _ {2} $ by applying a finite number of the elementary operations I–III shown in Fig. band isotopic deformations.

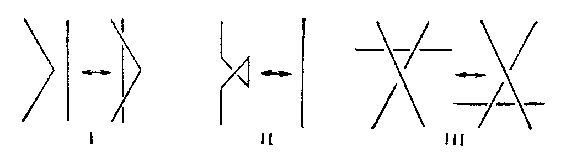
Figure: k055570b

The approach to knot theory established in this way is typical of combinatorial topology. It arose in the first period of development of knot theory (roughly up to the 1940's). In the framework of this approach invariants of knots were defined starting from diagrams and it was then proved that the result did not depend on the choice of a diagram (cf. [1]). In the modern development the definition of invariants is preferably given in terms of algebraic topology, which strips it in first instance from the geometric essence.

The diagram of an oriented link is used in the construction of its Seifert surface. Let $ x $ be any point, not double, of an oriented diagram $ D $ of a link $ k $. The diagram $ D $ is traversed in the direction of the given orientation, starting at $ x $. At the first encounter of a double point a turn is effected and the motion is continued in the direction of the orientation of $ D $ until one returns to $ x $; thus one has described a simple closed contour, called a Seifert circle. The diagram $ D $ is divided into these Seifert circles, $ C _ {j} $, which can only touch each other. For each circle $ C _ {j} $ one denotes by $ D _ {j} $ the disc lying in a plane parallel to $ \mathbf R ^ {2} $ such that its boundary projects onto $ C _ {j} $. For each double point $ \alpha _ {i} $ one considers the rectangle $ H _ {i} $ placed vertically on $ \alpha _ {i} $, twisted by $ 90 \circ $ so that the upper edge lies on the boundary of $ D _ {j _ {1} } $ and the lower on the boundary of $ D _ {j _ {2} } $, if $ C _ {j _ {1} } $ and $ C _ {j _ {2} } $ are the Seifert circles meeting in $ \alpha _ {i} $. If each turn is performed to the appropriate side, then the boundary arising from the surface $ F = \cup _ {j} D _ {j} \cup \cup _ {i} H _ {i} $ is isotopic to the link $ k $. The surface so obtained is orientable. A simpler, but possibly unorientable, surface spanned by the link may be obtained by putting a disc over each black area of the chess board diagram and adding, as above, turns through right angles.

Various methods are known for describing the presentations of the group of a link by its diagram. In order to obtain the Wirtinger presentation one considers the set of connected components $ t _ {1} \dots t _ {n} $ of the diagram of a link (the set of overpasses), numbered in the order of crossing each component of the link in the direction given by the orientation. Let $ \gamma _ {i} $ be a certain symbol associated with $ t _ {i} $. For each double point one has $ \gamma _ {i} = \gamma _ {j} \gamma _ {i+ 1} \gamma _ {j} ^ {- 1} $ or $ \gamma _ {i} = \gamma _ {j} ^ {- 1} \gamma _ {i+ 1} \gamma _ {j} $, depending on whether the diagram of the link in a neighbourhood of this double point has the form shown in Fig. 3a or Fig. 3b. The group given by the presentation with generators $ \gamma _ {1} \dots \gamma _ {n} $ (one for each overpass) and the above-mentioned defining relations (one for each double point) is isomorphic to the group of the link considered. The presentation so obtained is called the upper Wirtinger presentation. Dually one defines the lower Wirtinger presentation.

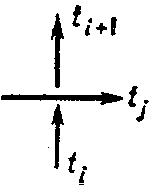
Figure: k055570c

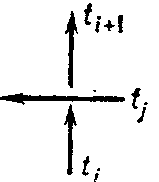
Figure: k055570d

To find the Dehn presentation one considers the domains $ f _ {i} $ into which the projection of the link divides the plane and introduces a symbol $ \overline{f}\; _ {i} $ for each domain $ f _ {i} $. The symbols $ \overline{f}\; _ {1} , \overline{f}\; _ {2} \dots $ are taken as generators, while the relations are obtained from traversal starting at the points $ \alpha _ {i} $: write in succession the symbols corresponding to the domains touching at $ \alpha _ {i} $, where if $ f _ {1} $ and $ f _ {2} $ lie on the left of an overpass, then the degrees of $ \overline{f}\; _ {1} $ and $ \overline{f}\; _ {3} $ are $ - 1 $ while $ f _ {2} $ and $ f _ {4} $ equal $ 1 $. Moreover, put $ \overline{f}\; _ {0} = 1 $, where $ f _ {0} $ is the exterior domain.

The use of knot and link diagrams to transform links into closed braids.

(Cf. Braid theory.) Choose a point $ o \in \Pi $ outside $ D $ such that the rays issuing from $ o $ contain no double points or segments from $ D $. A complete traversal of one of the components $ k _ {i} $ of the link can be effected as long as the corresponding traversal in the projection of $ k $ takes place in one and the same direction around $ o $. Let $ l $ be the first segment directed oppositely and let a point $ c $ be taken such that the triangle $ cab $, where $ a $ and $ b $ are the ends of $ l $, contains $ o $ in its interior and the sides $ ac $ and $ bc $ are in general position relative to $ D ( k) $. It can be shown that there is at most one double point on $ l $. Replace $ l $ in $ D ( k) $ by $ ac \cup bc $, where if $ l $ contains no double point or is an overpass, it is supposed that $ ac $ and $ bc $ are overpasses at all points of their intersection with $ D( k) $. If $ l $ has an underpass, one takes them to be underpasses. Extend this construction for $ k _ {i} $ and apply it in succession to all components; then a new diagram for $ k $ is obtained in which the projection of each component goes around $ o $ all the time on the same side, i.e. $ k $ is represented in the form of a closed braid [2].

Comments

Fig.a1 illustrates the construction of the Seifert surface: after the discs have been inserted, at each "split" double point, one has to insert a twisted band as indicated in Fig.a1.

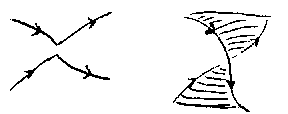
Figure: k055570e

For a detailed proof of Alexander's theorem that every link can be obtained as a closed braid cf. [a1], Chapt. II.

References

[1]	K. Reidemeister, "Knotentheorie" , Chelsea, reprint (1948)
[2]	J.W. Alexander, "A lemma on systems of knotted curves" Proc. Nat. Acad. Sci. USA , 9 (1923) pp. 93–95
[a1]	J.S. Birman, "Braids, links and mapping class groups" , Princeton Univ. Press (1975)
[a2]	L.H. Kauffman, "On knots" , Princeton Univ. Press (1987)
[a3]	R.H. Crowell, R.H. Fox, "Introduction to knot theory" , Ginn (1963)
[a4]	D. Rolfsen, "Knots and links" , Publish or Perish (1976)