Invariant set
of the phase space $ R $
of a dynamical system $ f ( p , t ) $
A set $ M $ which is the union of entire trajectories, that is, a set satisfying the condition
$$ f ( M , t ) = M ,\ t \in \mathbf R , $$
where $ f ( M , t ) $ is the image of $ M $ under the transformation $ p \mapsto f ( p , t ) $ corresponding to a given $ t $.
The invariant set $ M $ may possess a definite topological structure as a set of the metric space $ R $; for example, it can be a topological or smooth manifold, a surface, a closed Jordan curve, or an isolated point. One then says that the invariant set $ M $ is an invariant manifold, an invariant surface, an invariant curve, or an invariant point.
An invariant point is usually called a stationary point of the dynamical system, since for this point the motion reduces to rest: $ f ( p , t) = p $ for all values of $ t $. A closed invariant curve not containing any invariant points of the dynamical system is always formed by the trajectory of a periodic motion, that is, a motion satisfying the condition
$$ f ( p , t + T ) = f ( p , t ) $$
for all $ t \in \mathbf R $ and some $ T > 0 $. For this reason it is called a periodic trajectory. Examples which occur as invariant manifolds are a sphere, a torus and a disc; invariant surfaces — a cone, a Möbius strip and a sphere with handles; invariant sets — the set of all stationary points, the sets $ \Omega _ {p} $ and $ A _ {p} $ of all $ \omega $- and $ \alpha $- limit points of the motion $ f ( p , t ) $, respectively, and also the set $ W $ of all wandering points or the set $ R \setminus W $ of all non-wandering points (cf. Wandering point; Non-wandering point).
An invariant point of the dynamical system in the plane
$$ \tag{1 } \frac{dx}{dt} = f ( x , y ) ,\ \ \frac{dy}{dt} = g ( x , y ) $$
belongs to one of the following four types, according to the nature of the behaviour of the trajectories in a neighbourhood of it: a node, (Fig.a) a focus, (Fig.b) a saddle, (Fig.c) or a centre (Fig.d).
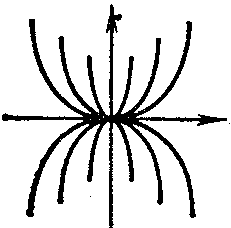
Figure: i052280a
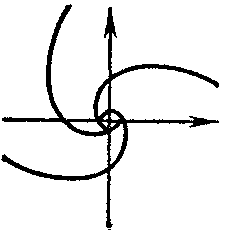
Figure: i052280b
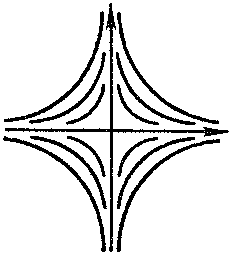
Figure: i052280c
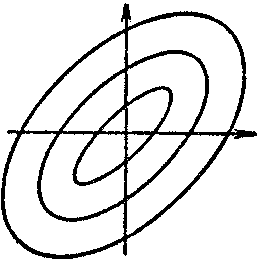
Figure: i052280d
The node and focus are asymptotically stable or unstable, the saddle is unstable, and the centre is stable (cf. Asymptotically-stable solution). The Poincaré index of the node, centre and focus is equal to $ + 1 $; that of the saddle is $ - 1 $.
In the case when the Jacobi matrix
$$ J ( x , y ) = \ \left ( \begin{array}{cc} \frac{\partial f ( x , y ) }{\partial x } & \frac{\partial f ( x , y ) }{\partial y } \\ \frac{\partial g ( x , y ) }{\partial x } & \frac{\partial g ( x , y ) }{\partial y } \\ \end{array} \right ) $$
of the right-hand side of (1) has at the stationary point $ x = x _ {0} , y = y _ {0} $ eigen values $ \lambda _ {1} $, $ \lambda _ {2} $ with non-zero real parts, the invariant point is: a node if $ \lambda _ {1} $ and $ \lambda _ {2} $ are real and of the same sign; a saddle if $ \lambda _ {1} $ and $ \lambda _ {2} $ are real with different signs; or a focus if $ \lambda _ {1} $ and $ \lambda _ {2} $ are complex conjugates.
In all these cases, the type of the singular point of the system (1) is the same as for the linear system obtained from (1) by expanding its right-hand side in a Taylor series at the point $ x = x _ {0} , y = y _ {0} $, that is, it has the same type as the point $ x _ {1} = 0 , y _ {1} = 0 $ of the system
$$ \tag{2 } \frac{d x _ {1} }{dt} = a x _ {1} + b y _ {1} ,\ \ \frac{d y _ {1} }{dt} = c x _ {1} + d y _ {1} , $$
whose matrix $ ( _ {c} ^ {a} {} _ {d} ^ {b} ) $ is equal to $ J ( x _ {0} , y _ {0} ) $. There is a deeper relation between the trajectories of (1) in a neighbourhood of a singular point of one of the above types and the trajectories of (2) than that already mentioned. Namely, whenever the functions $ f $ and $ g $ are analytic in a neighbourhood of the invariant point $ x = x _ {0} = 0 , y = y _ {0} = 0 $ and the matrix $ J ( x _ {0,\ } y _ {0} ) $ has eigen values with non-zero real parts, there exists a continuously-differentiable change of variables in a neighbourhood $ U $ of the point $ x = 0 , y = 0 $,
$$ x _ {1} = x + F _ {1} ( x , y ) ,\ \ y _ {1} = y + F _ {2} ( x , y ) , $$
$$ F _ {i} ( 0 , 0 ) = \frac{\partial F _ {i} ( 0 , 0 ) }{\partial x } = \frac{\partial F _ {i} ( 0 , 0 ) }{\partial y } = 0 ,\ i = 1 , 2 , $$
that reduces the system (1) to the system (2).
If $ \lambda _ {1} $, $ \lambda _ {2} $ are imaginary, then the invariant point $ x _ {0} , y _ {0} $ can either be a focus or a centre. In this case, the question of the classification of the type of the singular point is a separate and difficult problem, namely the centre and focus problem, and requires more refined criteria for distinguishing between the centre and the focus (see [1], [7]). Similar difficulties occur in the determination of the type of the singular point in the case when the matrix $ J ( x _ {0} , y _ {0} ) $ is singular.
References
| [1] | V.V. Nemytskii, V.V. Stepanov, "Qualitative theory of differential equations" , Princeton Univ. Press (1960) (Translated from Russian) MR0121520 Zbl 0089.29502 |
| [2] | G.D. Birkhoff, "Dynamical systems" , Amer. Math. Soc. (1927) MR1555257 Zbl 53.0733.03 Zbl 53.0732.01 |
| [3] | W.W. [V.V. Stepanov] Stepanow, "Lehrbuch der Differentialgleichungen" , Deutsch. Verlag Wissenschaft. (1956) (Translated from Russian) MR0087811 Zbl 0070.30603 |
| [4] | P. Hartman, "Ordinary differential equations" , Birkhäuser (1982) MR0658490 Zbl 0476.34002 |
| [5] | I.G. Malkin, "Theorie der Stabilität einer Bewegung" , R. Oldenbourg , München (1959) (Translated from Russian) MR0104029 Zbl 0124.30003 |
| [6] | A.M. Lyapunov, "Collected works" , 2 , Moscow-Leningrad (1956) (In Russian) MR0121296 MR0106812 MR0086006 |
| [7] | K.S. Sibirskii, "Algebraic invariance of differential equations and matrices" , Kishinev (1976) (In Russian) |
Comments
The reduction of the system (1) to the system (2) in a neighbourhood of a singular point is often called linearization of the equation. If $ \lambda _ {1} $ and $ \lambda _ {2} $ have non-zero real parts (in that case the singular point $ ( x _ {0} , y _ {0} ) $ is said to be of hyperbolic type) such a linearization can always be performed by means of a topological (non-smooth) coordinate transformation (i.e., the transformation and its converse are merely continuous), provided $ f $ and $ g $ in (1) are of class $ C ^ {1} $. This result holds also for autonomous differential equations in $ \mathbf R ^ {n} $ for $ n \geq 2 $. If certain "non-resonance" conditions between the eigen values are fulfilled, then one can also obtain smooth (under additional conditions even $ C ^ \infty $ or analytic) transformations (work of H. Poincaré, C.L. Siegel, S. Sternberg). See [4], pp. 256-271 and the references given in [4] on pp. 271-272. These results are related to the theory of normal forms for differential equations (cf. Normal form) and involve problems on small denominators.
For a description of the Poincaré index see Singular point.
Invariant set. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Invariant_set&oldid=47417