Small denominators

small divisors

Divisors of the form

$$ \tag{1 } i \langle P, \Omega \rangle + \langle Q, \Lambda \rangle \equiv $$

$$ \equiv \ i p _ {1} \omega _ {1} + \dots + i p _ {m} \omega _ {m} + q _ {1} \lambda _ {1} + \dots + q _ {n} \lambda _ {n} , $$

which appear in the coefficients of series obtained when integrating differential equations using Taylor series, Fourier series or Poisson series; here $ P = ( p _ {1} \dots p _ {m} ) $, $ Q = ( q _ {1} \dots q _ {n} ) $ are integer vectors, $ \Omega = ( \omega _ {1} \dots \omega _ {m} ) $ is a real vector, $ \Lambda = ( \lambda _ {1} \dots \lambda _ {n} ) $ is a complex vector, and $ \langle \cdot , \cdot \rangle $ denotes the scalar product. The existence of a solution and its properties, such as analyticity, smoothness, etc., depend essentially on the arithmetic nature of the numbers $ \omega _ {j} $, $ \lambda _ {k} $ and the same properties (analyticity, smoothness, etc.) of the differential equations. Conditions are given below which guarantee analyticity of solutions corresponding to analytic problems. These conditions are different for linear and non-linear problems.

1. Linear problems.

a) Taylor series. The solution $ \xi $ of the equation

$$ \sum _ {k = 1 } ^ { n } \frac{\partial \xi }{\partial x _ {k} } \lambda _ {k} x _ {k} = \ \phi ( X) \equiv \ \sum _ {\begin{array}{c} \langle Q, \Lambda \rangle \neq 0 \\ q _ {k} \geq 0 \end{array} } \phi _ {Q} x _ {1} ^ {q _ {1} } \dots x _ {n} ^ {q _ {n} } , $$

where $ X = ( x _ {1} \dots x _ {n} ) $ and $ \phi $ is analytic at $ X = 0 $( where $ \phi ( 0) = 0 $) and is expressed as the given Taylor series, is given by the Taylor series

$$ \xi = \sum \frac{\phi _ {Q} }{\langle Q, \Lambda \rangle } x _ {1} ^ {q _ {1} } \dots x _ {n} ^ {q _ {n} } . $$

This series converges in a neighbourhood of zero if there are $ \epsilon , \nu > 0 $ such that

$$ \tag{2 } | \langle Q, \Lambda \rangle | \geq \ \epsilon e ^ {- \nu | Q | } ,\ \ | Q | = | q _ {1} | + \dots + | q _ {n} |,\ \ $$

for all integer-valued $ Q \geq 0 $, $ \langle Q, \Lambda \rangle \neq 0 $. This condition is optimal in the class of all analytic functions $ \phi $; it is necessary for the convergence of the series $ \xi $.

b) Fourier series. The solution $ \eta $ of the equation

$$ \tag{3 } \sum _ {j = 1 } ^ { m } \frac{\partial \eta }{\partial y _ {j} } \omega _ {j} = \ \psi ( Y) \equiv \ \sum _ {\langle P, \Omega \rangle \neq 0 } \psi _ {P} \mathop{\rm exp} i \langle P, Y \rangle, $$

where $ Y = ( y _ {1} \dots y _ {m} ) $ and the right-hand side is expressed as a Fourier series, is given by the Fourier series

$$ \eta = \sum \frac{\psi _ {P} }{i \langle P, \Omega \rangle } \mathop{\rm exp} i \langle P, Y \rangle, $$

which converges in a strip $ | \mathop{\rm Im} Y | < \epsilon _ {0} $ if $ \psi $ is analytic and if

$$ \tag{4 } \lim\limits _ {| P| \rightarrow \infty } \ \frac{ \mathop{\rm ln} | \langle P, \Omega \rangle | }{| P | } \geq 0, $$

where the limit is taken over all integer-valued $ P $, $ \langle P, \Omega \rangle \neq 0 $. This condition is optimal in the class of all analytic functions $ \psi $ of the form (3).

Equation (3) arises in the reduction of a system of ordinary differential equations on a torus (see [1]; there (2) is erroneously given instead of (4)). The situation is similar when integrating with respect to $ t $ a conditionally-periodic function $ \psi ( \Omega t) $. Similar linear problems occur at each approximation in the iterated solution of non-linear problems (in perturbation theory).

If (2) or (4) are not satisfied, then the non-formal solution of the corresponding problem need not be analytic, smooth or need not exist at all (depending on the arithmetic properties of $ \Lambda $ and $ \Omega $), although formal solutions, the series $ \xi $ and $ \eta $, always exist (see [1]).

2. Non-linear problems.

In these problems small divisors (1) do not appear singly but in products.

a) Taylor series. Consider a system near a fixed point $ X = 0 $,

$$ \tag{5 } \dot{x} _ {j} = \ \lambda _ {j} x _ {j} + x _ {j} \phi _ {j} ( X),\ \ j = 1 \dots n, $$

where $ \phi _ {j} $ is a convergent Taylor series without free term. Let $ \langle Q, \Lambda \rangle \neq 0 $ for integer-valued $ Q \geq 0 $, $ Q \not\equiv 0 $. Then there is a formally invertible change of coordinates

$$ x _ {j} = \ u _ {j} + u _ {j} \xi _ {j} ( U),\ \ j = 1 \dots n, $$

where $ \xi _ {j} $ is also a Taylor series without free term, which transforms (5) to the normal form

$$ \tag{5'} \dot{u} _ {j} = \lambda _ {j} u _ {j} ,\ j= 1 \dots n. $$

The series $ \xi _ {j} $ converges in a neighbourhood of zero if

$$ \tag{6 } \sum _ {l = 1 } ^ \infty \frac{ \mathop{\rm ln} \beta _ {l} }{2 ^ {l} } > - \infty , $$

where $ \beta _ {l} = \min | \langle Q, \Lambda \rangle | $ for $ | Q | < 2 ^ {l} $, $ \langle Q, \Lambda \rangle \neq 0 $, $ Q \geq 0 $( see ).

Non-linear problems of this type were first solved by C.L. Siegel (1942; see , [3]) under the stricter condition:

$$ \tag{7 } | \langle Q, \Lambda \rangle | \geq \ \epsilon | Q | ^ {- \nu } . $$

Under this condition $ \mathop{\rm ln} \beta _ {l} \geq \mathop{\rm ln} \epsilon - l \nu \mathop{\rm ln} 2 $ and (6) converges. Condition (2) is equivalent to boundedness of the terms of (6); it is necessary for the convergence of $ \xi _ {j} $ for arbitrary analytic $ \phi _ {j} $. (In [8] necessity of condition (6) for $ n= 2 $ is claimed; for $ n > 2 $ it is unknown what happens in the "gap" between the conditions (2) and (6) (for more complicated resonance situations, see ).) If (2) is not satisfied, then between the solutions of (5) and its normal form (5'}) there need not be an analytic, a smooth or even a topological correspondence.

b) Poisson series. Let an analytic system

$$ \tag{8 } \left . \begin{array}{c} \dot{x} _ {j} = \ \lambda _ {j} x _ {j} + x _ {j} \sum \phi _ {jPQ} X ^ {Q} \mathop{\rm exp} i \langle P, Y \rangle, \\ \dot{y} _ {k} = \ \omega _ {k} + \sum \psi _ {kPQ} X ^ {Q} \ \mathop{\rm exp} i \langle P, Y \rangle, \\ X ^ {Q} = \ x _ {1} ^ {q _ {1} } \dots x _ {n} ^ {q _ {n} } ,\ \ j = 1 \dots n; \ \ k = 1 \dots m, \\ \end{array} \right \} $$

the right-hand sides of which are expanded as a Poisson series near the invariant torus $ X = 0 $( that is, a Taylor series with respect to $ X $ and a Fourier series with respect to $ Y $), have a formal integral manifold

$$ \tag{9 } x _ {j} = \ \eta _ {j} ( x _ {r + 1 } \dots x _ {n} , Y),\ \ j = 1 \dots r, $$

where $ \eta _ {j} $ is also a Poisson series. The question arises as to when this manifold is analytic (that is, when is $ \eta _ {j} $ absolutely convergent for sufficiently small $ | X | $ and $ | \mathop{\rm Im} Y | $). Here, among the $ x _ {j} $ there may be small parameters; for them $ \lambda _ {j} = 0 $. Such problems were first solved by A.N. Kolmogorov [4] for the Hamiltonian system (8) with $ m $ degrees of freedom and one small parameter $ x _ {n} $( that is, $ m + 1 = n $ and $ \Lambda = 0 $): Under the condition

$$ \tag{10 } | \langle P, \Omega \rangle | \geq \ \epsilon | P | ^ {- \nu } $$

the analyticity of the manifold (9), consisting of invariant tori, was proved for $ r = m $. At the same place it was suggested for the first time that "Newton's method" , which is fundamental in research into non-linear problems, be used for the proof of the convergence of the Poisson series $ \eta _ {j} $. Condition (10) and its analogue

$$ | i \langle P, \Omega \rangle + \langle Q, \Lambda \rangle | \geq \ \epsilon (| P | + | Q |) ^ {- \nu } $$

were then used in problems of the same type (see [5]–[7]). The conditions (2) and (4) are also necessary here for the convergence of (9) (for more complicated degenerate situations, see [7]). If these conditions are not satisfied, there need not be an analytic (or even continuous) invariant manifold of the form (9).

The most strict of the restrictions (2), (6), (7), condition (7), is, for $ \nu > n - 1 $, satisfied for almost-all (relative to Lebesgue measure) vectors $ \Lambda $. Properties of the type of (2), (6), (7) for vectors $ \Lambda $ are studied in the theory of Diophantine approximations. The two-dimensional case has been rather well studied. Let $ q _ {t} $ be the denominator of the $ l $- th convergent of the continued fraction of $ \lambda = \lambda _ {2} / \lambda _ {1} < 0 $. Then (6) is equivalent to convergence of the series

$$ \sum _ {l = 1 } ^ \infty \frac{ \mathop{\rm ln} q _ {l + 1 } }{q _ {l} } , $$

and (2) is equivalent to boundedness of its terms (see also [9], [10]).

Small divisors (1) with variable $ \Omega $ and $ \Lambda $ have been discussed (see [6]).

Small divisors were first encountered in celestial mechanics, and the fundamental linear problems were solved in 1884 by H. Bruns. In general, in the solar system there are many "points of commensurability" between frequencies, a consequence of which are the small divisors (1). For example, the small divisor $ 2 \omega _ {1} - 5 \omega _ {2} = 0.007 \dots $, where $ \omega _ {1} $ and $ \omega _ {2} $ are the frequencies of the motions of Jupiter and Saturn, respectively, leads to the appearance of large reciprocal perturbations in the motions of these planets. Another example: the gaps in the asteroid belt and in Saturn's rings correspond to resonance with the frequencies of the perturbing body (Jupiter and Mimas, respectively).

References

[1]	A.N. Kolmogorov, "On dynamical systems with integral invariant on a torus" Dokl. Akad. Nauk SSSR , 93 : 5 (1953) pp. 763–766 (In Russian)
[2a]	A.D. Bryuno, "Analytical form of differential equations" Trans. Moscow Math. Soc. , 25 (1971) pp. 131–288 Trudy Moskov. Mat. Obshch. , 25 (1971) pp. 119–262
[2b]	A.D. Bryuno, "Analytical form of differential equations" Trans. Moscow Math. Soc. , 26 (1972) pp. 199–239 Trudy Moskov. Mat. Obshch. , 26 (1972) pp. 199–239
[3]	C.L. Siegel, "Vorlesungen über Himmelsmechanik" , Springer (1956)
[4]	A.N. Kolmogorov, "On conservation of conditionally periodic motions for a small change in the Hamilton functions" Dokl. Akad. Nauk SSSR , 98 : 4 (1954) pp. 527–530 (In Russian)
[5]	J.K. Moser, "Lectures on Hamiltonian systems" , Amer. Math. Soc. (1968)
[6]	V.I. Arnol'd, "Small denominators and the problem of stability of motion in classical and celestial mechanics" Russian Math. Surveys , 18 : 6 (1963) pp. 86–191 Uspekhi Mat. Nauk , 18 : 6 (1963) pp. 91–192
[7]	A.D. Bryuno, "Local methods in nonlinear differential equations" , Springer (1989) (Translated from Russian)
[8]	J.Z. Yoccoz, "Linearisation des germs de diffeomorphismes holomorphes de 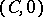" C.R. Acad. Sci. Paris , 306 (1988) pp. 55–58
[9]	A.D. [A.D. Bryuno] Bruno, "On small divisors" Banach Center Publications , 23 (1989) pp. 355–359
[10]	A.D. [A.D. Bryuno] Bruno, "A comparison of conditions on small divisors" Preprint IHES , 36 (1990)
[a1]	V.I. Arnol'd, "Mathematical methods of classical mechanics" , Springer (1978) (Translated from Russian)
[a2]	V.I. Arnol'd, V. Avez, "Ergodic problems of classical mechanics" , Benjamin (1968) (Translated from Russian)