Infinitesimal calculus

A term which formerly included various branches of mathematical analysis connected with the concept of an infinitely-small function. Even though the method of "infinitely smalls" had been successfully employed in various forms by the scientists of Ancient Greece and of Europe in the Middle Ages to solve problems in geometry and in natural science, exact definitions of the fundamental concepts of the theory of infinitely-small functions were laid only in the 19th century. In order to grasp the importance of this method, it must be pointed out that it was not the infinitesimal calculus itself which was of practical importance, but only the cases in which its use resulted in finite quantities. Three kinds of such problems were particularly important in the history of mathematics.

1) The simplest problems, solved by the mathematicians of Ancient Greece by the method of exhaustion (cf. Exhaustion, method of), in which infinitesimal quantities are used merely to prove that two given magnitudes (or two ratios between given magnitudes) are equal.

2) More sophisticated problems involving the method of exhaustion, in which the required finite magnitude is obtained as the limit of a sum

$$ \Delta _ {1} ^ {( n)} + \dots + \Delta _ {n} ^ {( n)} \ ( n \rightarrow \infty ) $$

of an infinitely-large number of infinitely-small quantities. These problems ultimately gave rise to integral calculus.

3) Problems in which the finite magnitude is obtained as the limit of ratios of infinitely-small magnitudes; they gave rise to differential calculus.

The invention of the method of exhaustion is attributed to Eudoxus of Cnidos (4th century B.C.). However this may be, the method is used throughout Book 12 of Euclid's Elements as the principal deductive tool. Euclid's chain of reasoning may be written in modern form as follows: If all the ratios

$$ { \frac{a _ 1}{b _ 1} } = \dots = \ { \frac{a _ n}{b _ n} } = \dots = k $$

are equal to each other and to a constant value $ k $, and if, as $ n \rightarrow \infty $, both differences $ a - a _ {n} $, $ b - b _ {n} $ become infinitely small, then

$$ { \frac{a}{b} } = k . $$

For instance, Euclid compares the areas of two discs by inscribing a square in each disc and proves that the area of this square is more than one-half of the area of the disc; therefore the remaining four segments together amount to less than half the area of the disc (cf. Fig. a); he then inscribes a regular octagon in the disc and notes that the area of the remainder is smaller than one-quarter of the area of the disc; he then inscribes a regular $ 16 $- gon and notes that the residual 16 segments together account for less than one-eighth of the area of the disc, etc. Thus, the area of the disc is gradually "exhausted" as the number of sides of the inscribed polygons increases. Since the ratio between the areas of the respective polygons inscribed in the two discs is equal to the ratio of the squares of the radii of the discs, Euclid concludes, by indirect proof, that the areas of the discs themselves are in the same ratio.

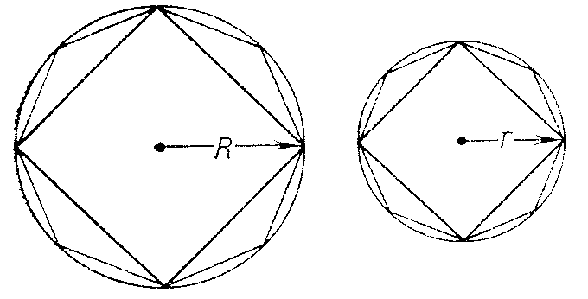
Figure: i050950a

A more extensive and freer use of infinitesimals was made by Archimedes (287–212 B.C.). In his work On conoids, spheroids and spirals Archimedes systematically computes areas and volumes by a method based on an idea which is exactly similar to the modern concept of the integral.

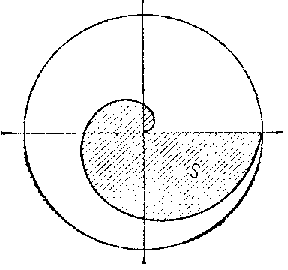
Figure: i050950b

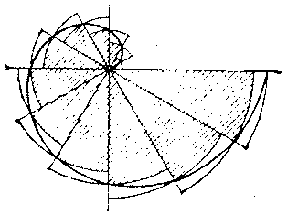
Figure: i050950c

For instance, Archimedes determines the area of the first coil of the spiral (Fig. b) which is now known as the Archimedean spiral, and the equation of which in polar coordinates is

$$ r = a \phi . $$

Into the figure $ S $ a figure consisting of $ n - 1 $ sectors of a disc with an angle of $ 2 \pi / n $ at the apex is inscribed (the shaded portion of Fig. crepresents these sectors for the case $ n = 12 $) while a figure consisting of $ n $ similar sectors of a disc is circumscribed around $ S $( the non-shaded areas in Fig. c). In both cases the formula for the area of an inscribed or a circumscribed sector has the form

$$ \frac{4 \pi ^ {3} a ^ {2} k ^ {2} }{n ^ {3} } $$

for appropriate $ k $. It is clear from the construction that the area of $ S $ is included between the bounds

$$ \tag{1 } S _ {n} ^ \prime < S < S _ {n} ^ {\prime\prime} , $$

where

$$ S _ {n} ^ \prime = \ \Delta _ {1} ^ {( n)} + \dots + \Delta _ {n - 1 } ^ {( n)} , $$

$$ S _ {n} ^ {\prime\prime} = \Delta _ {1} ^ {( n)} + \dots + \Delta _ {n} ^ {( n)} . $$

Since

$$ S _ {n} ^ \prime = \ 4 \pi ^ {3} a ^ {2} \frac{[ 1 ^ {2} + \dots + ( n - 1) ^ {2} ] }{n ^ {3} } = $$

$$ = \ 2 \pi ^ {3} a ^ {2} \frac{( n - 1) ( 2n - 1) }{3n ^ {2} } , $$

$$ S _ {n} ^ {\prime\prime} = 4 \pi ^ {3} a ^ {2} \frac{[ 1 ^ {2} + \dots + n ^ {2} ] }{n ^ {3} } = $$

$$ = \ 2 \pi ^ {3} a ^ {2} \frac{( n + 1) ( 2n + 1) }{3n ^ {2} } , $$

it follows that, for any $ n $,

$$ S _ {n} ^ \prime < { \frac{4}{3} } \pi ^ {3} a ^ {2} < S _ {n} ^ {\prime\prime} . $$

Archimedes expressed this last relation in geometrical form: For any $ n $,

$$ \tag{2 } S _ {n} ^ \prime < { \frac{K}{3} } < S _ {n} ^ {\prime\prime} , $$

where $ K $ is the area of the disc represented in Fig. b. On comparing (1) and (2), and in view of the fact that

$$ S _ {n} ^ {\prime\prime} - S _ {n} ^ \prime = \Delta _ {n} ^ {( n)} $$

becomes infinitely small as $ n \rightarrow \infty $, Archimedes concluded that

$$ S = { \frac{K}{3} } . $$

The end of the above reasoning shows how Eudoxus' exhaustion method was developed and improved by Archimedes, while its beginning shows that Archimedes was also familiar with the examples in the second group above, the meaning of which corresponds to the integral calculus.

The integral calculus yields the following value for the area in question:

$$ S = \int\limits _ { 0 } ^ { {2 } \pi } \frac{r ^ {2} }{2} d \phi = \ \int\limits _ { 0 } ^ { {2 } \pi } \frac{( a \phi ) ^ {2} }{2} d \phi = \ { \frac{4}{3} } \pi ^ {3} a ^ {2} . $$

By definition, the integral in this formula is the limit of sums of the form

$$ S _ {n} = \ \sum _ {k = 1 } ^ { n } \frac{r _ {k} ^ {2} }{2} ( \phi _ {k} - \phi _ {k - 1 } ), $$

where

$$ 0 = \phi _ {0} < \phi _ {1} < \dots < \phi _ {n} = 2 \pi , $$

$$ r _ {k} = av _ {k} ^ {2} ,\ \phi _ {k - 1 } \leq v _ {k} \leq \phi _ {k} . $$

In the particular case when

$$ \tag{3 } \phi _ {k} = \frac{2 \pi k }{n} , $$

$ v _ {k} = \phi _ {k- 1 } $ yields the Archimedean sum $ S _ {n} ^ \prime $, while $ v _ {k} = \phi _ {k} $ yields the Archimedean sum $ S _ {n} ^ {\prime\prime} $. It should be noted, in particular, that if the division points $ \phi _ {k} $ are chosen as in (3), the Archimedean sums $ S _ {n} ^ \prime $ and $ S _ {n} ^ {\prime\prime} $ are identical with the Darboux sums (cf. Darboux sum), for which inequality (1) is valid in the general case as well. It is seen that Archimedes employed several ways of perfect logical reasoning typical of the integral calculus (exact estimates from above and from below with the aid of Darboux sums), which were only merged into a general theory in the second half of the 19th century. Archimedes employed similar methods to solve other problems on the computation of areas and volumes.

It is seen that, towards the end of its development, ancient Greek mathematics also tackled problems belonging to the second group of problems indicated above. At the same time one must note the fundamental difference between the ways of thinking about the mathematical means of Antiquity and those of modern mathematicians. As an example, in solving the problem stated above, Archimedes does not compute

$$ S = \lim\limits _ {n \rightarrow \infty } S _ {n} = { \frac{K}{3} } , $$

but arbitrarily takes the value $ K/3 $ and gives an indirect proof of the equality $ S = K/3 $ by establishing that, in view of (1) and (2), and because the difference $ S _ {n} ^ {\prime\prime} - S _ {n} ^ \prime $ is infinitely small, the inequality $ S \neq K/3 $ would lead to a contradiction (his ideas were often motivated by "mechanical considerations" ). Greek mathematicians not only failed to develop any general rules for computing limits, but never even formulated the concept of the limit itself, on which their methods were based (even the general term "method of exhaustion" for these methods is a modern term). A fortiori, ancient science never produced anything resembling the modern algorithm of integral calculus, from which, as a result, in calculating a new integral by modern methods, one does not define it as a limit of sums, but uses much simpler and handier rules for the integration of functions belonging to different classes. The works of Archimedes (in particular, his Message to Eratosthenes) indicate that — prior to Archimedes' logically precise method for estimating areas and volumes with the aid of sums of a very large number of terms that are decreasing without limit (i.e. infinitesimals in the modern sense of the word) — there also existed a more primitive, but more illustrative method, attributable to Democritus (4th century B.C.). It is pointed out by Archimedes, in particular, that Democritus determined the volume of the pyramid prior to Eudoxus (even though he failed to give a rigorous proof of his results).

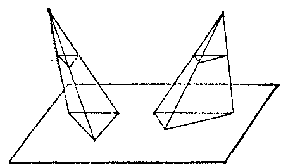
Figure: i050950d

In deriving the volume of a pyramid, the main difficulty encountered by Euclid and by Eudoxus was to prove that two pyramids with equal heights and equal base areas have equal volumes. Euclid overcame this difficulty in his Elements by using the method of exhaustion.

As reported by Archimedes, the "atomistic" method for proving the above theorem used by Democritus (Fig. d) may be described as follows. Similarity considerations indicate that the cross-sectional areas of the pyramids are equal at equal heights; the volume of the pyramids are simply considered as the "sums" of these areas; hence, the equalities of the corresponding terms of the two sums prove that the sums themselves are equal as well. Archimedes quotes many examples of the use of this method in solving more complicated problems. Archimedes considered the method not as strict but as highly valuable heuristically (i.e. for arriving at new results, which must subsequently be more rigorously demonstrated); from our own point of view, this view was undoubtedly correct, since Democritus' method was merely an unfounded attempt to replace the process of passing to a limit

$$ S = \lim\limits _ {n \rightarrow \infty } ( \Delta _ {1} ^ {( n)} + \dots + \Delta _ {n} ^ {(n)} ) $$

by the invalid metaphysical hypothesis to the effect that volumes can be added.

The message addressed by Archimedes to Eratosthenes, briefly named Ephodikon (handbook), was extensively quoted and commented upon by Hellenistic authors, but never reached European mathematicians during the creation of modern mathematics. Unaware of the unusually simple atomistic reasoning of Democritus, these mathematicians had to have recourse, at best, to the confused indications of other sources (the text of Ephodikon was only rediscovered in 1906). Nevertheless, the method was brilliantly developed by J. Kepler (1517–1630) and by B. Cavalieri (1598–1647) in the 17th century. In his Stereometria doliorum (volume measurement of wine barrels) (1615) Kepler determined the volume of 92 bodies of revolution. Had he pedantically followed Archimedes' reasoning in each such determination, the size of his work would have been enormous. Kepler's method can be explained by means of a simple example. His determination of the area of a disc is based on the following reasoning. The disc is subdivided into sectors with common apex at the centre (Fig. e); the narrower each sector, the closer it resembles a triangle, the base of which may be considered to be the cord of the sector; its area is therefore equal to the product of the length of the cord and one-half of the radius; if these areas are summed, the area of the disc is equal to the length of its circumference, multiplied by half its radius.

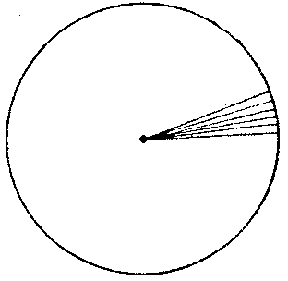
Figure: i050950e

The volume of a sphere and other bodies of revolution are equally simple; however, this very simplicity is open to doubt (as admitted by Kepler himself) and is in fact responsible for a number of errors. In order to eliminate such doubts, Kepler justifies his reasoning concerning the area of a disc as follows: The constituent sectors may be made so small that their bases become single points, and the number of sectors becomes infinite; each one of these infinitely-small sectors will then have become perfectly equal to the corresponding triangle. Clearly, this proves nothing at all, since if the base becomes a single point, there are no more sectors, and the triangle simply becomes a radius. The special feature of this reasoning consists in the fact that Kepler tends, consciously or subconsciously, to adopt the statical decomposition of the disc into an infinitely-large number of actual infinitely-small sectors (radii), rather than the potential infinity of a continuously-increasing number of continuously-decreasing terms; in this form the unboundedness of the process ceases to be. It would be incorrect to say that Kepler had firmly come down on the side of the actual infinity; he was in fact greatly influenced by Archimedes, with whose principal works he was thoroughly familiar, but his views on the question are eclectic. His views give a transition to the views of Cavalieri.

Figure: i050950f

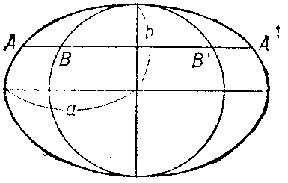
Figure: i050950g

The treatise of Cavalieri: Geometria indivisibilibus (continuorum nova quadam ratione promota) (geometry, exposed in a new manner with the aid of indivisibles of the continuous) appeared in 1635. Cavalieri set himself the same task as did Archimedes — to calculate the surface areas and volumes of figures of arbitrary shape. Cavalieri considers a plane figure as a set of parallel rectilinear segments extending from one extremal tangent to the other (Fig. f), and a solid figure as the set of its planar sections. These segments and planar sections are the "indivisibles" after which Cavalieri's method is named (cf. Indivisibles, method of). The measurement of surfaces and volumes is realized by comparing the indivisibles of two figures. For instance, Cavalieri computes the surface area of an ellipse with the aid of the following reasoning (Fig. g). Draw a circle around the small axis of the ellipse ( $ 2b $) and draw the (indivisible) cords parallel to the large axis ( $ 2a $). It can be easily shown, on the strength of the definition of the ellipse, that the ratio between each indivisible element of the ellipse to the corresponding element of the circle is as $ a $ to $ b $, i.e. $ AA ^ \prime : B B ^ \prime = a : b $. Accordingly, the ratio between the union of all the indivisibles of the ellipse (i.e. the surface area of the ellipse) and the union of the indivisibles of the circle (the area $ \pi b ^ {2} $) is equal to $ a : b $; the surface area of the ellipse is accordingly $ \pi a b $. Cavalieri applied the same methods to the comparison of volumes; Cavalieri's proof that two pyramids having the same base areas and the same heights are equal terminates at the point where Archimedes' proof only begins. The general applicability and the simplicity of Cavalieri's methods yielded results which could not be obtained by Archimedes. However, the fact that a method is simple is no guarantee of its correctness, and for this reason Cavalieri conducted each one of his computations by several independent paths.

While Cavalieri's work is much inferior to that of Archimedes as regards the rigour of proofs of his results, it is much superior to that of Archimedes and ancient mathematicians in general, not only as regards the number of special problems in determining surface areas and volumes solved, but also as regards his understanding of the future potential of the science of infinitesimals. As well as solving individual problems, Cavalieri obtained a number of general formulas of integral calculus, albeit only in a loose, geometrical form.

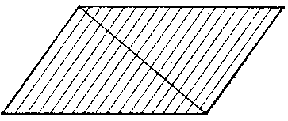
Figure: i050950h

For instance, Cavalieri's postulate to the effect that the sum of the squares of the indivisibles constituting the parallelogram in Fig. his equal to three times the sum of the squares of the indivisibles comprised in each of the two triangles which constitute this parallelogram, is in fact identical with the formula

$$ \int\limits _ { 0 } ^ { a } x ^ {2} dx = \frac{1}{3} \int\limits _ { 0 } ^ { a } a ^ {2} \ dx = \frac{a ^ {3} }{3} . $$

Cavalieri adopted a similar method to express the equality

$$ \int\limits _ { 0 } ^ { a } x ^ {n} dx = \frac{a ^ {n+ 1} }{n+ 1 } $$

for values of $ n $ of up to 9 inclusive.

Mathematicians of the 17th century also studied the third group of problems specified above. Following the creation of analytic geometry by R. Descartes (1596–1650), a problem which naturally arose was the determination of the angular coefficient of the tangent to a curve $ y = f( x) $, i.e. the determination of the derivative. At about the same time the development of mechanics necessitated the calculation of the instantaneous rate of arbitrary motion of a point, i.e. again the problem of determining the derivative. Since the theory of limits and even a clear understanding of limit transition were lacking at that time, it was attempted to compute the derivative

$$ f ^ { \prime } ( x) = \lim\limits _ {\Delta x \rightarrow \infty } \frac{\Delta y }{\Delta x } $$

as the ratio

$$ f ^ { \prime } ( x) = \frac{dy}{dx} $$

of the actually infinitesimal increments $ dy $ and $ dx $.

The modern concept of infinitesimals as variable magnitudes tending to zero, and of the derivative as the limit of the ratio of infinitely-small increments, was proposed by I. Newton (1642–1727), though not fully rigorously, but became properly established after A.L. Cauchy (1789–1857). The modern concept of a differential as the principal part of the increment must be credited to J.L. Lagrange (1736–1813), and was finally fixed by Cauchy; the latter also gave a rigorous definition of an integral as a limit of sums.

A typical feature of modern differential and integral calculus is the fact that, after its fundamental ideas have been rigorously established by means of limit transition, it yields solutions of a wide variety of problems by means of purely algebraic algorithms (in the sense that the algorithm itself no longer contains the explicit operation of limit transition). As a result, modern differential and integral calculus represent a successful synthesis of mathematical rigour with simplicity and clarity.

References

[1]	I.L. Heiberg (ed.) , Archimedes: Opera Omnia , Wissenschaft. Buchgesellschaft , Darmstadt (1972)
[2]	M. Casper (ed.) , J. Keppler: Gesammelte Werke , C.H. Beck (1937)
[3]	B. Cavalieri, "Geometria indivisibilibus (continuorum nova quadam ratione promota)" , Bologna (1635)

Comments

Concerning Euclid's Elements see $ Elements $ of Euclid.

References

[a1]	G. Becker, "Das mathematische Denken der Antike" , Göttingen (1966)
[a2]	C.B. Boyer, "The history of the calculus and its conceptual development" , Dover (1959)
[a3]	C.H. Edwards, "The historical development of the calculus" , Springer (1979)
[a4]	E.S. Stamatis (ed.) , Euclides: Elementa , Leipzig (1969)
[a5]	T.L. Heath, "The thirteen books of Euclid's elements" , Dover, reprint (1956) ((Translated from the Greek))
[a6]	L. Euler, "Einleitung in die Analysis des Unendlichen" , Springer, reprint (1983) (Translated from Latin)
[a7]	W.R. Knorr, "The evolution of the Euclidean elements" , Reidel (1975)
[a8]	A. Robinson, "Nonstandard analysis" , North-Holland (1966)
[a9]	I. Schneider, "Archimedes" , Wissenschaft. Buchgesellschaft , Darmstadt (1979)