Hopf manifold

A complex Hopf manifold is a quotient of $\mathbf C ^ {n} \setminus \{ 0 \}$ by the infinite cyclic group of holomorphic transformations generated by $z \mapsto \lambda z$, $\lambda \in \mathbf C \setminus \{ 0 \}$, $| \lambda | \neq 1$. It is usually denoted by $\mathbf C H _ \lambda ^ {n}$. As a differentiable manifold, any $\mathbf C H _ \lambda ^ {n}$ is diffeomorphic to $S ^ {2n - 1 } \times S ^ {1}$. Consequently, when $n \geq 2$ the first Betti number $b _ {1} ( \mathbf C H _ \lambda ^ {n} ) = 1$; hence, such $\mathbf C H _ \lambda ^ {n}$ provide examples of compact complex manifolds (cf. Complex manifold) not admitting any Kähler metric (note that, for $n = 1$, $\mathbf C H _ \lambda ^ {1}$ is a $1$- dimensional complex torus). However, these manifolds do carry a particularly interesting class of Hermitian metrics (cf. Hermitian metric), namely locally conformal Kähler metrics (a Hermitian metric is locally conformal Kähler if its fundamental $2$- form $\Omega$ satisfies the integrability condition $d \Omega = \omega \wedge \Omega$ with a closed $1$- form $\omega$, called the Lee form). An example of such a metric is the projection of the following metric on $\mathbf C ^ {n} \setminus \{ 0 \}$: $g _ {0} = | z | ^ {- 2 } \delta _ {jk } dz ^ {j} \otimes d {\overline{z}\; } ^ {k}$, whose Lee form is $\omega _ {0} = | z | ^ {- 2 } \sum ( z ^ {j} d {\overline{z}\; } ^ {j} + {\overline{z}\; } ^ {j} dz ^ {j} )$. It is parallel with respect to the Levi-Civita connection of $g _ {0}$. This originated the study of the more general class of generalized Hopf manifolds: locally conformal Kähler manifolds with parallel Lee form. Their geometry is closely related to Sasakian and Kählerian geometries. Generically, a compact generalized Hopf manifold arises as the total space of a flat, principal $S ^ {1}$ bundle over a compact Sasakian orbifold and, on the other hand, fibres into $1$- dimensional complex tori over a Kähler orbifold.

I. Vaisman conjectured that a compact locally conformal Kähler manifold that is not globally conformal Kähler must have an odd Betti number. To date (1996), this has only been proved for generalized Hopf manifolds (see [a5]).

It is rather difficult to characterize the Hopf manifolds among the locally conformal Kähler manifolds. However, in complex dimension $2$ several such characterizations are available; for instance, the only compact complex surface with $b _ {1} = 1$ and admitting conformally flat Hermitian metrics is $\mathbf C H _ \lambda ^ {2}$( cf. [a4]; see also [a1]).

By analogy, "real Hopf manifoldreal Hopf manifolds" were defined as (compact) quotients of $\mathbf R ^ {n} \setminus \{ 0 \}$ by an appropriate group of conformal transformations (see [a6] and [a2]). Similarly, "quaternion Hopf manifoldquaternion Hopf manifolds" are defined as quotients of $\mathbf H ^ {n} \setminus \{ 0 \}$( see [a3]).

References

[a1]	C.P. Boyer, "Conformal duality and compact complex surfaces" Math. Ann. , 274 (1986) pp. 517–526
[a2]	P. Gauduchon, "Structures de Weyl–Einstein, espaces de twisteurs et variétés de type 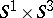" J. Reine Angew. Math. , 455 (1995) pp. 1–50
[a3]	L. Ornea, P. Piccinni, "Locally conformal Kähler structures in quaternionic geometry" Trans. Amer. Math. Soc. , 349 (1997) pp. 641–655
[a4]	M. Pontecorvo, "Uniformization of conformally flat Hermitian surfaces" Diff. Geom. Appl. , 3 (1992) pp. 295–305
[a5]	I. Vaisman, "Generalized Hopf manifolds" Geom. Dedicata , 13 (1982) pp. 231–255
[a6]	I. Vaisman, C. Reischer, "Local similarity manifolds" Ann. Mat. Pura Appl. , 35 (1983) pp. 279–292
[a7]	S. Dragomir, L. Ornea, "Locally conformal Kähler geometry" , Birkhäuser (1997)