Functional system
A set of functions with some collection of operations that can be applied to these functions and that lead to other functions of this set. Functional systems are one of the basic objects of mathematical cybernetics and discrete mathematics, and reflect the following principal features of real and abstract control systems (cf. Control system): the functioning (in a functional system this is given by the functions), a rule for constructing more complex control systems from given ones, and a description of the functioning of complex systems in terms of the functioning of their components (the last two features are reflected in the operations of a functional system). Examples of functional systems are many-valued logic, automaton algebras, algebras of computable functions (cf. Computable function), and others. A functional system has a certain specific character, consisting in considering problems and approaches arising in the investigation of functional systems from the points of view of mathematical cybernetics, mathematical logic and algebra. Thus, from the point of view of mathematical cybernetics, functional systems are regarded as models describing the functioning of complex cybernetic systems; from the point of view of mathematical logic, as models of logics, that is, as systems of propositions with logical operations on them; and from the point of view of algebra, as universal algebras.
An important feature of functional systems that distinguishes them from the general class of universal algebras is their substantial connection with real cybernetic models of control systems. This connection, on the one hand, determines a number of essential requirements that are imposed on functional systems, and on the other hand gives rise to a class of important problems having both theoretical and practical importance. The problems of functional systems are extensive, and have much in common with the problems of many-valued logic. Among the most important problems for functional systems are those of completeness, of the complexity of expressing some functions in terms of others, of identical transformations, of synthesis and analysis, and others.
The study of functional systems is carried out by means of the investigation of concrete models of functional systems, among which one of the first to be studied was two-valued and three-valued, and then also $ k $- valued, logic. As well as these, automaton algebras were intensively studied, such as functional systems of functions with delays, of finitely-determined functions and determined functions (cf. Finitely-determined function), of countably-valued logics, of computable functions, of inhomogeneous functions, and others.
As well as collecting models of functional systems and studying their properties, general concepts of functional systems have been elaborated, and functional systems have been analyzed from the point of view of solving the problems mentioned above for them. One can also consider universal algebras as generalized real functional systems, but in this case one loses the main virtues of real functional systems, above all those such as the constructive nature of the sets and operations, and a number of others.
The following approach to understanding functional systems is of sufficient generality. The essence of the approach consists in considering pairs of the form $ \langle \mathfrak M , \Omega \rangle $, where $ \mathfrak M $ is a set of functions of a $ k $- valued or countably-valued logic or a set of sequential functions, or also a set of some generalizations of such functions (for example, partial or inhomogeneous functions, etc.), and where $ \Omega $ is a set of operations (like on automata) which must have the same properties as were imposed on the operations in the examples of functional systems mentioned: this is both the local nature of the information about the functions that can be used in applying the operations to the functions, and the computable character of the operations, with a definite sense of computability by simplest, i.e. automaton, means, and the constructive nature of the way the functions themselves are given, etc. The actual concept of a functional system as associated with real functional systems splits into the concepts of a truth-value functional system and a sequential functional system. In the first case, the set $ \mathfrak M $ in $ \langle \mathfrak M , \Omega \rangle $ consists of functions of many-valued logic, and in the second, of sequential functions, that is, functions operating on words. All real functional systems turn out to be either truth-valued or sequential functional systems.
An important role in the study of functional systems is played by the closure operator $ I _ \Omega $ that is associated with a functional system $ \langle \mathfrak M , \Omega \rangle $ if one regards it as a partial universal algebra. This operator, and also the operators in $ \Omega $, are called automaton operators. It has been established that the classes of automaton and algebraic closure operators coincide. This implies, in particular, that all real functional systems are also truth-value or sequential functional systems from the formal point of view.
References
| [1] | S.V. Yablonskii, "Functional constructions in 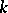 -valued logic" Trudy Mat. Inst. Steklov. , 51 (1958) pp. 5–142 (In Russian) -valued logic" Trudy Mat. Inst. Steklov. , 51 (1958) pp. 5–142 (In Russian) |
| [2] | S.V. Yablonskii, Nauchn. Sov. Akad. Nauk SSSR Kibernet. Informat. Mat. , 5 (42) (1970) pp. 5–15 |
| [3] | S.V. Yablonskii, "On certain results in the theory of functional systems" , Proc. Internat. Congress Mathematicians (Helsinki, 1978) , Acad. Sci. Fennicae (1980) pp. 963–971 (In Russian) |
| [4] | E.L. Post, "Two-valued iterative systems of mathematical logic" , Princeton Univ. Press (1941) |
| [5] | V.B. Kudryavtsev, "Functional systems" , Moscow (1982) (In Russian) |
Comments
Systems theory, as a branch of applied mathematics, also deals with functional systems. See, for instance, [a1]; [a2] provides a coherent mathematical presentation of the theory of automata and the theory of formal languages.
References
| [a1] | J.C. Willems, "From time series to linear system - part I. Finite dimensional linear time invariant systems" Automatica , 22 : 5 (1986) pp. 561–580 |
| [a2] | S. Eilenberg, "Automata, languages and machines" , 1–2 , Acad. Press (1974) |
Functional system. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Functional_system&oldid=47017