Many-valued logic
A branch of mathematical logic studying mathematical models of propositional calculus. These models reflect the two fundamental features of the latter: the plurality of truth values of propositions, and the possibility of constructing new, more complicated, propositions from given ones using logical operations, which also allow the truth values of the compound propositions to be established with respect to the truth values of initial propositions. Examples of many-valued propositions are statements with a modal outcome ( "yes" , "no" , "may be" ) and statements of a probabilistic nature; examples of logical operations are logical connectives of the type "and" , "or" , "if … then" . In general, models of many-valued logic are generalizations of the algebra of logic. It is important to note that in the algebra of logic, propositions take only two truth values ( "yes" , "no" ); thus, in general, they may not reflect the full variety of logical structures encountered in practice. In a fairly broad interpretation of many-valued logic, logical calculi (cf. Logical calculus) are also sometimes included.
Historically, the first models of many-valued logics were the two-valued logic of G. Boole (mid 19th century), also called the algebra of logic, the three-valued logic of J. Łucasiewicz (1920) and the $ m $- valued logic of E. Post (1921). The investigation of these models was an important stage in the development of the theory of many-valued logics.
Basic models of many-valued logics.
Many-valued logics have a specific distinguishing feature, which is the discussion of the problems and methods arising in the investigation of many-valued logics from the point of view of mathematical logic, mathematical cybernetics and algebra. Thus, from the point of view of mathematical cybernetics, models of many-valued logics are considered as languages describing the functioning of complex control systems the components of which may be in a certain number of different states, and from the point of view of algebra, models of many-valued logics are algebraic systems (cf. Algebraic system) having both applied and theoretical interest.
The construction of models of many-valued logics is done by analogy with the construction of a two-valued logic. Thus the individual propositions of the logic, separated into classes with the same truth value, lead to the idea of a set $ E $, a constant of the model, which in fact identifies all individual propositions, replacing them by their corresponding truth values; variable propositions become variable quantities $ x _ {1} , x _ {2} \dots $ which take values in $ E $; the logical connectives become elements of a set $ M $ of elementary functions (operations) the arguments of which take values from $ E $. Compound propositions, constructed from individual and variable propositions and also the logical connectives, become elements of the set $ \langle M \rangle $ of formulas over $ M $. The truth value from $ E $ of a compound proposition is a function of the corresponding truth values of the propositions figuring in the given compound proposition. In the model this function is associated with a formula corresponding to the given compound proposition; the formula is also said to realise the function. Functions mapping a tuple of elements of $ E $ into $ E $ are called functions of $ m $- valued logic, where $ m $ denotes the cardinality of the set $ E $. The set of all functions of $ m $- valued logic is denoted by $ P _ {m} $. The set of formulas $ \langle M \rangle $ leads to a set $ [ M ] $ of functions realizing the formulas from $ \langle M \rangle $ called superpositions (or compositions) over $ M $. The set $ [ M ] $ is called the closure of the set $ M $. The specification of the concrete model of a many-valued logic $ M _ {F} $ is to be regarded as equivalent to indicating the sets $ E $, $ M $, $ \langle M \rangle $, and $ [ M ] $; the model is then said to be generated by $ M $; if $ M $ is finite, the model is called finitely generated. This model is called a formula model, and also an $ m $- valued logic.
The distinctive approach of mathematical cybernetics to many-valued logics is to regard models of many-valued logics as control systems. The elementary functions here are the elements producing the operations, and formulas are interpreted as schemes constructed from the elements which also process input information into output. Control systems of this kind, known in cybernetics as diagrams of functional elements (without branching), are widely utilized in theoretical and practical questions of cybernetics.
At the same time there are a number of problems of logic and cybernetics connected with the study of relationships between the sets $ M $ and $ [ M ] $ in which the role of $ \langle M\rangle $ is somewhat in the background, regarded just as a means of defining the second set from the first. This situation leads to another model of a many-valued logic as an algebra whose elements are functions taking values and arguments from $ E $. It is common to use as operations in this algebra a special set of operations equivalent in meaning to the relationship of $ M $ and $ [ M ] $ to the set of formulas constructed from functions on $ M $; that is, compound functions are obtained from single functions whose arguments are other functions. These algebras are called the algebras of $ m $- valued logic. They may be arrived at concretely, for example, by the introduction of the following one-place operations: $ \zeta , \tau , \Delta , \nabla $, and a binary operation $ \star $. If one assumes that, taking into account fictitious variables, each function $ f $ from $ P _ {E} $ depends on $ x _ {1} \dots x _ {n} $, where $ n $ is determined by $ f $, then these operations can be given as:
$$ ( \zeta f ) ( x _ {1} \dots x _ {n} ) = \ f ( x _ {2} \dots x _ {n} , x _ {1} ) , $$
$$ ( \tau f ) ( x _ {1} \dots x _ {n} ) = f ( x _ {2} , x _ {1} , x _ {3} \dots x _ {n} ) , $$
$$ ( \Delta f ) ( x _ {1} \dots x _ {n-1} ) = f ( x _ {1} , x _ {1} , x _ {2} \dots x _ {n-1} ) $$
if $ n > 1 $, and $ \zeta f = \tau f = \Delta f = f $ if $ n = 1 $;
$$ ( \nabla f ) ( x _ {1} \dots x _ {n} , x _ {n+1} ) = f ( x _ {2} , x _ {3} \dots x _ {n+1} ) $$
and for $ f ( x _ {1} \dots x _ {n} ) $ and $ g ( x _ {1} \dots x _ {m} ) $,
$$ ( f \star g ) ( x _ {1} \dots x _ {n+m- 1} ) = $$
$$ = \ f ( g ( x _ {1} \dots x _ {m} ) , x _ {m+1} \dots x _ {m+n- 1} ) . $$
The algebras $ M _ {E} = \langle M , \zeta , \tau , \Delta , \nabla , \star \rangle $ are sometimes called Post algebras.
Problems in many-valued logic.
Among the problems characteristic of formula models of many-valued logics is the problem of "description" , that is, the question of giving all formulas of $ \langle M _ {1} \rangle $ which realise functions from $ M _ {2} $, for a given set $ M _ {2} \subseteq [ M _ {1} ] $. A particular case of this problem is the important question in mathematical logic of giving all formulas which realise a given constant; for example, in propositional calculus, this is equivalent to the construction of all identically-true propositions.
A question at the interface between mathematical logic and algebra, related to the problem of description, is the problem of identical transformations. Here for a given $ M $ it is required to select the simplest, in some sense, subset of pairs of equal (i.e. realizing the same function) formulas from $ \langle M \rangle $( identities) which by substitution of one formula for the other allows one to obtain from any formula all formulas equal to it (a complete system of identities).
A similar place is occupied by the so-called completeness problem, which is to give all subsets $ M _ {1} $ of a given closed (i.e. equal to its closure) set $ M $ for which $ [ M _ {1} ] = M $; that is, the completeness property (or the functional completeness property) of $ M _ {1} $ in $ M $ holds. Close to this problem is the basis problem, which is to give each complete subset $ M _ {1} $ in $ M $ no proper subset of which is complete in $ M $; complete independent systems of functions are also called bases. There are two approaches to the solution of the completeness problem — the algorithmic and the algebraic. In the first case there is the question of the existence of an algorithm which establishes the completeness or incompleteness of a system of functions described in some language; in the second, one passes to the study of the properties of the lattice of subalgebras of a given algebra of $ m $- valued logic and solves the completeness question using these properties. An important idea in the algebraic approach is that of a criterial system of subalgebras. A system $ N $ of subalgebras of an algebra $ M = \langle M , \zeta , \tau , \Delta , \nabla , \star \rangle $ is called criterial if the following property holds: A set $ M ^ { \prime } \subseteq M $ is complete if and only if it is not a subset of any subalgebra in $ N $. For example, the set of all proper subalgebras of the algebra $ M $ is criterial. In general, the latter criterial system is too large. Each criterial system contains all maximal subalgebras of the algebra $ M $( all pre-complete classes), and this enables one to move to the consideration of more economical criterial systems which do not contain subalgebras of maximal subalgebras. Thus, in completeness problems one may confine oneself to the use of criterial systems of the form $ N = \Sigma _ {1} \cup \Sigma _ {2} $, where $ \Sigma _ {1} $ is the set of all maximal subalgebras and $ \Sigma _ {2} $ consists of some of those subalgebras that are not subalgebras of any maximal subalgebra. If $ \Sigma _ {2} $ is empty, then the completeness problem reduces to the description of all maximal subalgebras of the algebra $ N $.
A global problem in many-valued logics is the description of the lattice of closed classes of a given model of a many-valued logic.
The characteristic question in the theory of complexity of control systems arises naturally in relation to the formulas and functions from a many-valued logic. Typical for this approach is the following problem on the complexity of realization. By some means a numerical measure (the complexity of a formula) is introduced on the set of all elementary formulas; it is then extended to the set of all formulas, for example, by summing the measures of all elementary formulas entering in a given formula. For a given function it is required to give the (simplest) formula which realizes the function with least complexity, and also to clarify how this complexity depends on the properties of the function considered. Various generalizations of the problem have been studied.
There is a wide circle of questions connected with the realization of functions by formulas with preassigned properties. Here one has the problem on the realization of functions of the algebra of logic by disjunctive normal forms (cf. Disjunctive normal form) and the related minimization problem; also there is the problem of the realization of functions by formulas which have bounded depth (that is, by formulas in which the chain of formulas substituted in each other has bounded length, this bound being connected with realizability and speed of calculation), the decomposition problem, that is, the realization of functions of variables using formulas constructed from elementary formulas which realize functions of fewer variables, and a number of other problems.
The solution of all the problems above depends essentially on the cardinalities of the sets $ E $ and $ M $ generating the given model of the many-valued logic.
The most important examples of many-valued logics.
The most important examples of many-valued logics are the finite-valued logics (that is, $ m $- valued logics for which $ m $ is finite). For these it is common to assume that $ E = E _ {m} = \{ 0 \dots m - 1 \} $, and the $ m $- valued logic $ M _ {E} $ is denoted by $ M _ {m} $. The case $ m = 2 $ has been investigated most deeply; here the functions are also called Boolean functions (cf. Boolean function). The most important result is the complete description, by Post (see [1]), of the lattice of closed classes. Their set turns out to be countable, and each class and the lattice of classes, ordered by inclusion, can be effectively constructed. These classes are called Post classes. Each closed class has a finite basis of cardinality not exceeding 4. These results lead to solutions of the problems on description, completeness and bases, and also of the problem on identical transformations. With respect to complete finite systems, for "almost-all" functions the behaviour of the measure of complexity of the simplest formulas realizing these functions has been given and corresponding algorithms for the synthesis of the formulas have been constructed (see [2]). The problem of the construction of optimal formulas with respect to complexity, realizing functions reliably and sufficiently quickly, and also the question of the complexity of realization for a large number of special classes of functions and individual functions have been studied.
One of the intensively researched problems for two-valued logics is the minimization problem. Here a special language for the specification of the functions of a two-valued logic — the language of disjunctive normal forms — has been studied. The idea of the complexity of a disjunctive normal form, the number of letters in it, has been introduced, and the problems connected with the finding, construction and metric properties of the disjunctive normal form that is "simplest" in the sense of this measure and that realizes a given function have been investigated (see [3]). The decomposition problem of Boolean functions is the clarification of conditions under which a given function of $ n $ variables may be realized by a formula constructed from functions of fewer variables, where all functions substituted into each other during the construction of the formula do not depend on common variables. Such formulas are called non-iterative. It has been shown that there is no finite system of functions such that each function can be realized by a non-iterative formula over this system, and even that "almost-all" functions do not have a realization by non-iterative formulas. On the whole, two-valued logics, because of special properties, are the main objects in which the general formulation of problems is discussed.
For arbitrary finite-valued logics, which for $ m > 2 $ are essentially different from two-valued logics, there are effective solutions of the problems on description for finite systems. It has been shown that for $ m \geq 3 $ there are $ m $- valued logics with a finite basis and which, at the same time, do not have a finite complete system of identities (see [4]), whereas in two-valued logics each closed class has a finite complete system of identities (see [5]). For finite-valued logics with a finite basis there is an effective solution of the completeness problem. It is obtained in the following way. One says that a function $ f ( x _ {1} \dots x _ {n} ) $ preserves a set $ K = \{ g _ {1} ( x _ {1} \dots x _ {n} ) \dots g _ {s} ( x _ {1} \dots x _ {n} ) \} $ if for any set $ g _ {i _ {1} } \dots g _ {i _ {k} } $, where $ g _ {i _ {j} } \in K $, one has $ f ( g _ {i _ {1} } \dots g _ {i _ {k} } ) \in K $. A set $ K $ is called regular if the choice function $ g _ {j} ( x _ {1} \dots x _ {n} ) = x _ {j} $ is contained in $ K $ for all $ j $, $ 1 \leq j \leq n $, and if each function from $ K $ preserves $ K $. If $ M = [ K ] $, then in $ M $ one selects all systems $ K ^ \prime $ with the following properties: the functions in them depend only on $ x _ {1} \dots x _ {n} $; the addition to them of all choice functions makes these systems regular; they do not contain $ K $ as a subset. This procedure of selection of all regular sets $ K _ {1} \dots K _ {t} $, $ t \leq 2 ^ {m ^ {n} } $, is effective. The system $ \{ U ( K _ {1} ) \dots U ( K _ {t} ) \} $, where $ U ( K _ {i} ) $( the preservation class of $ K _ {i} $) consists of all functions from $ M $ which preserve $ K _ {i} $, $ 1 \leq i \leq t $, is criterial. Inclusion of an arbitrary finite set $ K \subseteq M $ in each of the classes $ U ( K _ {i} ) $ can also be verified effectively. Each pre-complete class is a preservation class and the set of all pre-complete classes in this case forms a criterial system. It has been shown that for $ m \geq 3 $ there is a continuum of closed classes in $ P _ {m} $, and that there exist closed classes with bases of given finite or infinite cardinality, and also classes which do not have bases; here the families of classes without a basis, or with a countable basis, have the cardinality of the continuum. Examples of classes without a basis or having a countable basis are $ [ \{ f _ {0} \dots f _ {n} ,\dots \} ] $ or $ [ \{ g _ {1} \dots g _ {n} ,\dots \} ] $, where $ f _ {n} \equiv 0 $ for $ n = 0 $ and for $ n > 0 $, $ f _ {n} ( x _ {1} \dots x _ {n} ) $ is equal to $ 0 $ on all collections except $ ( 2 \dots 2 ) $, at which it is equal to $ 1 $; $ g _ {n} ( x _ {1} \dots x _ {n} ) $ is equal to $ 0 $ on all collections except the collections of the form $ ( 2 \dots 2 , 1 , 2 \dots 2 ) $ at which it is equal to 1 (see [6]).
The completeness problem in the $ m $- valued logic $ P _ {m} $ is of particular interest. In $ P _ {m} $ there are finite complete systems; this allows one to select a finite complete subsystem for each complete system and to reduce the problem to the study of finite complete systems. There also exist complete systems consisting of one function; such functions are called Sheffer functions. An example is the Wenn function $ \max ( x _ {1} , x _ {2} ) + 1 $( $ \mathop{\rm mod} m $). Because of finite generation, the completeness problem in $ P _ {m} $ can be solved effectively.
In $ P _ {m} $ all pre-complete classes, which are preservation classes for special predicates, have been effectively constructed. Giving these predicates forms the content of the completeness theorem in finite-valued logics (see [7]). One says that a function $ f ( x _ {1} \dots x _ {n} ) $ preserves a predicate $ R : ( E _ {m} ) ^ {h} \rightarrow \{ 0 , 1 \} $ if the formula
$$ R ( z _ {11} \dots z _ {1h} ) \& \dots \& R ( z _ {n1} \dots z _ {nh} ) \rightarrow $$
$$ \rightarrow \ R ( f ( z _ {11} \dots z _ {n1} ) \dots f ( z _ {1h} \dots z _ {nh} ) ) $$
is identically equal to 1 for all values of the variables $ z _ {ij} $, $ 1 \leq i \leq n $, $ 1 \leq j \leq h $. The class $ U ( R) $ of all functions preserving a predicate $ R $ is called the preservation class of the predicate $ R $. It has been shown that for each pre-complete class $ N $ it is possible to choose a predicate $ R $, depending on at most $ m + 2 $ variables, and for $ m \geq 3 $ on at most $ m $ variables, such that $ N = U ( R) $. These predicates may be partitioned into six families: $ H , S , E , L , Z , U $. The families $ H $, $ S $ and $ E $ consist of all two-place predicates or order relations on $ E _ {m} $ having one maximal and one minimal element in the first case; giving permutations on $ E _ {m} $ which decompose into cycles of identical prime number length (without invariant elements) in the second case; and giving non-identity and non-universal equivalence relations on $ E _ {m} $ in the third case. The family $ L $ is not empty for $ m = p ^ {k} $, $ p $ a prime, and consists of all four-place predicates $ R _ {G} ( y _ {1} , y _ {2} , y _ {3} , y _ {4} ) $ for which $ R _ {G} ( y _ {1} , y _ {2} , y _ {3} , y _ {4} ) = 1 $ is equivalent to $ y _ {1} + y _ {2} = y _ {3} + y _ {4} $, where $ G $ is an Abelian group in which each non-zero element has order $ p $. The predicate $ R ( y _ {1} \dots y _ {h} ) $, $ 1 \leq h \leq m $, is reflexive if the fact that not all the numbers $ a _ {1} \dots a _ {h} $ are distinct implies that $ R ( a _ {1} \dots a _ {h} ) = 1 $. It is symmetric if for any permutation $ s $ of $ 1 \dots h $ one has $ R ( y _ {1} \dots y _ {h} ) = R ( y _ {s(} 1) \dots y _ {s(} h)) $; the set of elements $ c \in E _ {m} $ for which $ R ( a _ {1} \dots a _ {h-1} , c ) = 1 $ for any $ a _ {1} \dots a _ {h-1} $ is called the centre of the symmetric predicate $ R $. A predicate $ R $ is central if it is reflexive, symmetric and has a centre $ c $ such that $ \emptyset \subset c \subset E _ {m} $. The family $ Z $ consists of all $ h $- place central predicates such that $ 1 \leq h \leq m $. For an $ a $ from $ E _ {h ^ {k} } $ one puts $ a = \sum_{l=0}^ {k-1} [ a ] _ {l} \cdot h ^ {l} $, where $ [ a ] _ {l} \in E _ {k} $. The family $ U $ consists of all predicates $ R ( y _ {1} \dots y _ {h} ) $, $ 3 \leq h \leq m $, $ h ^ {k} \leq m $, $ k \geq 1 $, such that for some surjection $ \phi : E _ {m} \rightarrow E _ {h ^ {k} } $ the equality $ R ( a _ {1} \dots a _ {h} ) = 1 $ is equivalent to the collections $ ( [ \phi ( a _ {1} ) ] _ {l} \dots [ \phi ( a _ {n} ) ] _ {l} ) $ being the same for $ l = 0 \dots k - 1 $. It has been established that predicates from different families give different pre-complete classes, and conditions have been given under which predicates from the same family give the same classes. It has been shown that the number of pre-complete classes is asymptotically equal to $ \delta ( m) \cdot m \cdot 2 ^ {a(} m) $, $ a ( m) = ( {} _ {[ ( m - 1 ) / 2 ] } ^ { m- 1 } ) $, where $ \delta ( m) = 1 $ if $ m $ is even and $ \delta ( m) = 2 $ if $ m $ is odd (that is, this number grows fairly rapidly), which is an indication of the small practical effectiveness of criterial systems (see [8]). Various modifications of the completeness problem have been discussed, leading to the investigation of systems with certain a priori known properties; for example, systems containing the set $ P _ {m} ^ {1} $ of all one-place functions, or the set $ S _ {m} $ of all permutations. In the first case for $ m > 2 $, and in the second for $ m > 4 $, the system is complete if and only if it contains an essential function, that is, a function depending on more than one variable and taking all $ m $ values (see [9], [10]). Related to this is the problem of giving all subsets $ T $ of $ P _ {m} ^ {1} $ and $ S _ {m} $, each of which, together with any essential function, forms a complete system. It has been shown that the subset $ T \subseteq P _ {m} ^ {1} $ of all one-place functions not taking at least one value is such a subset, while the subset $ T \subseteq P _ {m} ^ {1} $ of all one-place functions not taking at least two values is, in general, already not one of these. For $ m > 4 $ they are precisely the subsets $ T $ which are: $ 4 $- transitive for $ m = 2 ^ {k} $; $ 3 $- transitive for $ m = p ^ {k} $, $ p $ prime, $ p \neq 2 $; and $ 2 $- transitive for the remaining $ m $. These conditions, with a natural generalization of transitivity, hold for arbitrary systems of functions which take all $ m $ values (see [11]).
For systems consisting of one function, the completeness criterion is the $ 2 $- transitivity condition. For $ m > 2 $ an arbitrary set of functions is complete if and only if it is $ m $- transitive and if the degree of transitivity cannot be reduced.
From finite complete systems, by identification, it is possible to transfer to a simpler class of complete systems, called simple bases. By a simple basis is meant a finite complete system which loses the completeness property after identification of any pair of essential variables in any function of the system. There are only a finite number $ q $ of simple bases and $ \mathop{\rm log} q \sim m ^ {m ^ {m-1} - ( m - 1 ) ! } $[12]. The number of variables in functions from simple bases does not exceed $ m ^ {m-1} $, and there are functions in a simple basis which essentially depend on $ m ^ {m-1} $ variables. Representations of the many-valued logic $ P _ {k} $ in $ P _ {m} $, that is, homomorphisms of $ P _ {k} $ to $ P _ {m} $, have been given [13]; some analogues of the minimization theory have also been constructed for arbitrary finite-valued logics.
The first example of finite-valued logics were the $ 3 $- valued logic of Łucasiewicz generated by the functions $ 1 - x $, $ \min ( 1 , 1 - x _ {1} - x _ {2} ) $, where $ x _ {1} , x _ {2} $ take the values $ 0 , 1 / 2 , 1 $, and the $ m $- valued logic of Post generated by the functions $ x _ {1} + 1 $( $ \mathop{\rm mod} m $), $ \max ( x _ {1} , x _ {2} ) $, where $ x _ {1} , x _ {2} $ take the values $ 0 \dots m - 1 $. Bordering on the subject of finite-valued logics is the topic of algebras of many-valued functions to which, to a significant extent, the problems and methods of research of finite-valued logics have been transferred.
Examples of other many-valued logics are countable-valued and continuum-valued logics (that is, $ m $- valued logics whose cardinality $ m $ is, respectively, countable or that of the continuum). These models play an important role in mathematical logic, model theory and mathematical analysis. For countable-valued logics it has been established that the set of pre-complete (and thus the set of all) closed classes has a cardinality higher than that of the continuum, and the solution of the completeness problem for systems containing the set $ P _ {\aleph _ {0} } ^ {1} $ of all one-place functions has been found [14]. In contrast to finite-valued logics $ P _ {m} $ for $ m > 2 $, where there is only one pre-complete class containing all one-place functions, in $ P _ {\aleph _ {0} } $ there are two such pre-complete classes, and a given system of functions is complete if and only if it is not contained in these classes. If one generalizes the notion of an essential function to be a function which forms a complete system together with $ P _ {\aleph _ {0} } ^ {1} $, then, just as in finite-valued logics, there is the problem of describing all subsets of $ P _ {\aleph _ {0} } ^ {1} $ that contain the set $ S _ {\aleph _ {0} } $ of permutations from $ P _ {\aleph _ {0} } $ and that together with any essential function form a complete system. It has been shown that the intersection of all such closed subsets itself has the property mentioned. This intersection, which is different from $ S _ {\aleph _ {0} } $, has been effectively described in set-theoretical terms.
In countable-valued and continuum-valued logics a special role is played by various subclasses. Such are, in the first case, limit logics, and, in the second case, many-valued logics of continuous functions. Limit logics are countable closed classes of functions of the many-valued logic $ P _ {\aleph _ {0} } $ which contain homomorphic inverse images of all finite-valued logics. There is a continuum of distinct, and even finitely-generated, pairwise non-isomorphic limit logics. It has been established that the completeness problem for limit logics, in general, is not equivalent to finding all pre-complete classes. The cardinality of the set of pre-complete classes in limit logics may be any natural number and also may be countable or of the cardinality of the continuum (see [15]). For many-valued logics of continuous functions the completeness of all two-place functions has been proved, and an analogue of the theorem on the completeness of systems consisting of all one-place and many-place functions has been obtained. It has also been established that every continuous function can be represented as the sum of specially chosen continuous one-place functions. It has been shown that $ k $- times differentiable functions of $ n $ variables, in general, cannot be represented using superpositions of functions of the same smoothness but depending on fewer variables (see [16]).
It is also possible to attribute to many-valued logics algebras of functions in which the collection of operations is somewhat different from those described above. Such are algebras of non-homogeneous finite-valued functions (their arguments take a finite number of values from their domains), recursive and partial recursive functions, algebras of automata mappings, and a number of others.
References
| [1] | S.V. Yablonskii, G.P. Gavrilov, V.B. Kudryavtsev, "Functions of the algebra of logic and Post classes" , Moscow (1964) (In Russian) |
| [2] | O.B. Lupanov, "On an approach to synthesis of control systems—the local coding principle" Probl. Kibernetiki , 14 (1965) pp. 31–110 (In Russian) |
| [3] | Yu.I. Zhuravlev, "Set-theoretical methods in the algebra of logic" Probl. Kibernetiki , 8 (1962) pp. 5–44 (In Russian) |
| [4] | R.K. Lyndon, "Identities in two-valued calculi" Kibernet. Sb. , 1 (1960) pp. 234–245 (In Russian) MR0044470 Zbl 0044.00201 |
| [5] | V.L. Murskii, "The existence in the three-valued logic of a closed class with finite basis, not having a finite complete system of identities" Soviet Math. Dokl. , 6 : 4 (1965) pp. 1020–1024 Dokl. Akad. Nauk SSSR , 163 : 4 (1965) pp. 815–818 MR186539 |
| [6] | Yu.I. Yanov, A.A. Muchnik, "On the existence of 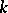 -valued closed classes without finite basis" Dokl. Akad. Nauk SSSR , 127 : 1 (1959) pp. 44–46 (In Russian) -valued closed classes without finite basis" Dokl. Akad. Nauk SSSR , 127 : 1 (1959) pp. 44–46 (In Russian) |
| [7] | I. Rosenberg, "Ueber die funktionale Vollständigkeit in den mehrwertigen Logiken" , Chechoslovak. Akad. (1970) Zbl 0199.30201 |
| [8] | E.Yu. Zakharova, V.B. Kudryavtsev, S.V. Yablonskii, "Precomplete classes in 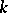 -valued logics" Soviet Math. Dokl. , 10 : 3 (1969) pp. 618–622 Dokl. Akad. Nauk SSSR , 186 : 3 (1969) pp. 509–512 -valued logics" Soviet Math. Dokl. , 10 : 3 (1969) pp. 618–622 Dokl. Akad. Nauk SSSR , 186 : 3 (1969) pp. 509–512 |
| [9] | S.V. Yablonskii, "Functional constructions in 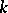 -valued logic" Trudy Mat. Inst. Steklov. , 51 (1958) pp. 5–142 (In Russian) -valued logic" Trudy Mat. Inst. Steklov. , 51 (1958) pp. 5–142 (In Russian) |
| [10] | A. Salomaa, "Some completeness criteria for sets of functions over a finite domain II" Turun Yliopiston Julkaisuja , AI : 63 (1963) MR0153576 Zbl 0143.24802 Zbl 0113.00305 |
| [11] | V.B. Kudryavtsev, "The properties of 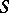 -systems of functions of -systems of functions of 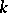 -valued logic" Elektron. Informationverarb. und Kybernetik (EIK) , 9 : 1–2 (1973) pp. 81–105 (In Russian) (English and German abstracts) -valued logic" Elektron. Informationverarb. und Kybernetik (EIK) , 9 : 1–2 (1973) pp. 81–105 (In Russian) (English and German abstracts) |
| [12] | V.B. Alekseev, "On the number of simple bases in 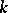 -valued logic" Diskretn. Anal. : 19 (1971) pp. 3–10 (In Russian) -valued logic" Diskretn. Anal. : 19 (1971) pp. 3–10 (In Russian) |
| [13] | A.I. Mal'tsev, "Iterative algebras and Post varieties" Algebra i Logika , 5 : 2 (1966) pp. 5–24 (In Russian) |
| [14] | G.P. Gavrilov, "On functional completeness in countable-valued logic" Probl. Kibernetiki , 15 (1965) pp. 5–64 (In Russian) |
| [15] | Ya. Demetrovich, "On certain homomorphisms and relations for limit logics" Probl. Kibernetiki , 30 (1975) pp. 5–42 (In Russian) |
| [16] | A.G. Vitushkin, "On the possibility of representing a function by a superposition of functions of fewer variables" , Proc. International Congress Mathematicians Moscow, 1966 , Moscow (1968) pp. 322–328 (In Russian) |
| [a1] | A. Urquhart, "Many-valued logic" D. Gabbay (ed.) F. Guenther (ed.) , Handbook of philosophical logic , III , Reidel (1986) pp. 71–116 MR1884631 MR0938721 MR0313021 Zbl 0875.03054 |
| [a2] | N. Rescher, "Many-valued logic" , McGraw-Hill (1969) MR0174475 Zbl 0248.02023 |
Many-valued logic. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Many-valued_logic&oldid=55121