Extension of an operator
A linear operator whose graph contains the graph of the given linear operator. When the operator $ B $
is an extension of a given operator $ A $,
one writes $ A \subset B $.
The usual problems in the theory of extensions are as follows: extend an operator maximally while preserving a specific property, or study extensions of an operator having various additional properties.
For example, let $ A $ be a given isometric operator on a Hilbert space $ H $ with domain of definition $ D ( A) \subset H $ and range of values $ R ( A) \subset H $; then the isometric extensions of $ A $ are in one-to-one correspondence with the isometric mappings from $ H _ {+} = D ( A) ^ \perp $ to $ H _ {-} = R ( A) ^ \perp $. In particular, $ A $ has unitary extensions if the dimensions of $ H _ {+} $ and $ H _ {-} $ coincide.
Extensions of symmetric operators.
The most studied (and most important in applications) is the theory of self-adjoint extensions of symmetric operators on a Hilbert space. An operator $ T $ is symmetric if and only if $ T \subset T ^ {*} $, where $ T ^ {*} $ is the operator adjoint to $ T $. Thus, the domain of definition of any symmetric extension of $ T $ is contained in $ D ( T ^ {*} ) $, and these extensions are restrictions of $ T ^ {*} $. This reduces the description of the symmetric extensions of $ T $ to determining their domains of definition. A subspace $ L \subset D ( T ^ {*} ) $ is the domain of definition of some symmetric extension of $ T $ if and only if $ ( T ^ {*} x, y) = ( x, T ^ {*} y) $ for all $ x, y \in L $. It turns out that
$$ D ( T ^ {*} ) = \ D ( T) \dot{+} N _ {+} \dot{+} N _ {-} , $$
where $ N _ \pm = \mathop{\rm Ker} ( T ^ {*} \mps \mathop{\rm id} ) $ are deficiency subspaces (defect subspaces) (their dimensions $ n _ \pm = \mathop{\rm dim} N _ \pm $ are called deficiency numbers (defect numbers)), and the symmetric extensions of $ T $ are in one-to-one correspondence with the isometric mappings from $ N _ {+} $ to $ N _ {-} $: To any such mapping $ V $ corresponds an extension of $ T $ with domain of definition $ D ( T) \dot{+} \Gamma _ {V} $, where $ \Gamma _ {V} $ is the graph of $ V $. Self-adjoint extensions correspond to unitary operators $ V $, and hence exist if and only if the defect numbers are equal.
The domains of definition of extensions of symmetric operators can be conveniently described with the help of so-called (abstract) boundary conditions. Any linear functional on $ D ( T ^ {*} ) $, continuous relative to the norm $ \langle x \rangle = ( \| x \| ^ {2} + \| T ^ {*} x \| ^ {2} ) ^ {1/2} $, and equal to zero on $ D ( T) $, is called a boundary value for the symmetric operator $ T $; an equation $ f ( x) = 0 $, where $ f $ is a boundary value, is called a boundary condition. Boundary values are determined by their values on $ N _ {+} \dot{+} N _ {-} $. If the defect numbers of a symmetric operator $ T $ are finite, then each of its symmetric extensions $ \widetilde{T} $ is determined by a family of boundary conditions, that is, $ D ( \widetilde{T} ) = \cap _ {i = 1 } ^ {k} \mathop{\rm Ker} f _ {i} $, where $ f _ {i} $ are boundary values. The families of boundary values determining self-adjoint extensions of $ T $ with defect numbers $ n _ {+} = n _ {-} = n $ can be described as follows. Let $ \phi _ {1} \dots \phi _ {n} $ and $ \psi _ {1} \dots \psi _ {n} $ be orthonormal bases of $ N _ {+} $ and $ N _ {-} $, respectively, and let, for $ 1 \leq i \leq n $,
$$ f _ {i} ( x) = \ ( T ^ {*} x, \phi _ {i} ) - ( x, T ^ {*} \phi _ {i} ), $$
$$ g _ {i} ( x) = ( T ^ {*} x, \psi _ {i} ) - ( x, T ^ {*} \psi _ {i} ). $$
Then any self-adjoint extension $ \widetilde{T} $ of $ T $ is determined by the boundary conditions
$$ D ( \widetilde{T} ) = \ \cap _ {i = 1 } ^ { k } \mathop{\rm Ker} \left ( f _ {i} - \sum _ {j = 1 } ^ { n } \theta _ {ij} g _ {j} \right ) , $$
where $ ( \theta _ {ij} ) _ {i,j=} 1 ^ {n} $ is a unitary $ ( n \times n) $- matrix.
In some cases one can successfully prove the existence of self-adjoint extensions (and find some of them) without solving the difficult problem of determining the defect subspaces and defect numbers. For example, if $ T $ commutes with an (anti-unitary) involution of the space $ H $, then it has a self-adjoint extension. This is often used in the theory of differential operators, where the involution is taken to be complex conjugation in the space $ L _ {2} $. Equality of defect numbers also occurs in the case when $ T $ has points of regular type on the real axis ( $ \lambda $ is called a point of regular type if $ \| Tx - \lambda x \| \geq c \| x \| $ for some $ c > 0 $ and for all $ x \in D ( T) $).
Extensions of semi-bounded operators.
An operator $ T $ is called semi-bounded from below by $ a \in \mathbf R $ if its numerical range $ \{ {( Tx, x) } : {\| x \| = 1, x \in D ( T) } \} $ lies in the interval $ ( a, \infty ) $; an operator is called positive if it is semi-bounded from below by zero. If $ T $ is semi-bounded from below by $ a $, then every $ \lambda < a $ is a point of regular type, the defect numbers are equal and self-adjoint extensions exist. One such an extension can be constructed as follows. The sesquilinear form $ q _ {T} ( x, y) = ( Tx, y) $ defined on $ D ( T) \times D ( T) $ admits a closure $ \overline{q}\; _ {T} $. But, being a closed symmetric bilinear form, to $ \overline{q}\; _ {T} $ corresponds a unique self-adjoint operator $ \widehat{T} $ such that $ q _ {\widehat{T} } \subset \overline{q}\; _ {T} $. The operator $ \widehat{T} $ is called the Friedrichs extension of the operator $ T $ and is semi-bounded. The greatest lower bound of its spectrum is equal to the greatest lower bound of the numerical range of $ T $. This is the unique self-adjoint extension whose domain of definition is contained in the domain of definition of $ \overline{q}\; _ {T} $. Using the Friedrichs extension it is possible to describe other semi-bounded extensions of $ T $( if the defect numbers of $ T $ are finite, then all its self-adjoint extensions are semi-bounded). For this it is sufficient to find all positive extensions of positive operators (the general case reduces to this by adding a multiple of the identity operator). Let $ T $ be a positive operator and let $ L = \mathop{\rm Ker} T ^ {*} $. Then the positive self-adjoint extensions of $ T $ correspond uniquely to positive bounded operators $ B $ on $ L $; for every such operator $ B $, the subspace $ D ( T) \dot{+} ( \widehat{T} {} ^ {-} 1 + B) L $ is the domain of definition of the corresponding extension (see ).
The construction of the Friedrichs extension can be generalized to the case of sectorial operators, i.e. operators whose numerical range is contained in some angle $ \{ {z \in \mathbf C } : {| \mathop{\rm arg} ( z - z _ {0} ) | \leq \theta < \pi /2 } \} $. There is an extension, which is a maximal sectorial operator, whose numerical range lies in the same angle and which, like the Friedrichs extension, is minimal. The case of operators from a Banach space into its dual space has also been studied (see [5]).
Dissipative extensions.
In some problems it is necessary to construct symmetric extensions of symmetric operators. A typical result is as follows. An operator $ A $ is called dissipative if its numerical range lies in the left half-plane, and maximal dissipative if it is dissipative and does not have dissipative extensions. Every symmetric operator has an extension of the form $ iA $, where $ A $ is a maximal dissipative operator; all such extensions can be described by means of contractive mappings of $ N _ {+} $ into $ N _ {-} $( see [8]).
Extensions of differential operators.
The theory of extensions of operators has important applications in the study of differential operators. Let
$$ l ( y) = \ \sum _ {i = 0 } ^ { n } (- 1) ^ {n - i } ( p _ {i} ( x) y ^ {( n - i) } ) ^ {( n - i) } $$
be a formal self-adjoint differential expression on the interval $ ( a, b) $, let $ D \subset L _ {2} ( a, b) $ be the subspace consisting of all functions with absolutely-continuous quasi-derivatives of orders $ 0 \dots 2n - 1 $, and $ 2n $- th quasi-derivative in $ L _ {2} ( a, b) $, and let $ D _ {0} $ be the subspace of $ D $ consisting of the functions whose supports do not contain the end points of the intervals. Let $ T $ be the operator given by $ Ty = l ( y) $ for $ y \in D $, and let $ T _ {0} ^ { \prime } $ be its restriction to $ D _ {0} $. Then $ T _ {0} ^ { \prime } $ is symmetric, $ T _ {0} ^ { \prime* } = T $; let $ T _ {0} = T _ {0} ^ { \prime } $ be its closure. In the regular case (that is, when the interval $ ( a, b) $ is finite and the function $ 1/p _ {0} $ is summable), the domain of definition of $ T _ {0} $ is formed by all functions in $ D $ whose first $ 2n - 1 $ quasi-derivatives vanish at the end points of the interval. In the singular case, $ D ( T _ {0} ) $ is harder to describe (see [2]). The defect numbers of $ T _ {0} $ coincide and are equal to $ 2n $ in the regular case and are at most $ 2n $ in the singular case. Thus, $ T _ {0} $ always has self-adjoint extensions; their spectra, spectral decompositions and resolvents are the basic objects of study in the theory of differential operators, because the choice of this or that self-adjoint extension is in fact the precise formulation of a certain spectral problem. This is particularly clear in the regular case, when the (abstract) boundary conditions, giving the domain of definition of a self-adjoint extension of $ T _ {0} $, are written in the form of ordinary boundary conditions:
$$ \sum _ {k = 1 } ^ { 2n } \alpha _ {jk} y ^ {[ k - 1] } ( a) + \sum _ {k = 1 } ^ { 2n } \beta _ {jk} y ^ {[ k - 1] } ( b) = 0,\ \ j = 1 \dots 2n, $$
for some $ \alpha _ {ik} $, $ \beta _ {ik} $( this follows from the above description of (abstract) boundary conditions since, in the regular case, the boundary values are determined by $ \phi _ {j} ( y) = y ^ {[} j] ( a) $, $ \psi _ {j} ( y) = y ^ {[} j] ( b) $).
For $ p _ {0} ( x) > 0 $, $ T _ {0} $ is semi-bounded from below, and its Friedrichs extension corresponds to the boundary conditions $ y ^ {[} j] ( a) = y ^ {[} j] ( b) = 0 $, $ 0 \leq j \leq 2n - 1 $.
In the general case, the self-adjoint extensions of $ T _ {0} $ can be characterized as follows. Let
$$ [ y, z] = \ \sum _ {k = 1 } ^ { n } ( y ^ {[ k - 1] } \overline{z}\; {} ^ {[ 2n - k] } - y ^ {[ 2n - k] } \overline{z}\; {} ^ {[ k - 1] } ) $$
for all functions $ y $ and $ z $ from $ D $. Then the limits
$$ \lim\limits _ {x \rightarrow a } \ [ y, z] _ {x} = \ [ y, z] _ {a} ,\ \ \lim\limits _ {x \rightarrow b } \ [ y, z] ( x) = \ [ y, z] _ {b} $$
exist and satisfy
$$ [ y, z] _ {b} - [ y, z] _ {a} = \ ( Ty, z) - ( y, Tz) $$
(Lagrange's formula). Thus, to describe the self-adjoint extensions of $ T _ {0} $ it is sufficient to choose bases $ \phi _ {1} \dots \phi _ {n} $ and $ \psi _ {1} \dots \psi _ {n} $ of the defect subspaces $ N _ {+} $ and $ N _ {-} $( it is convenient to assume that $ \psi _ {i} = \overline \phi \; _ {i} $) and to put every unitary matrix $ ( \theta _ {ij} ) _ {i,j=} 1 ^ {n} $ into correspondence with the self-adjoint extension $ T _ \theta $ whose domain of definition consists of all functions $ y \in D $ that satisfy the boundary conditions
$$ [ y, \xi _ {j} ] _ {b} - [ y, \xi _ {j} ] _ {a} = 0,\ \ 1 \leq j \leq n, $$
where
$$ \xi _ {j} = \phi _ {j} - \sum _ {i = 1 } ^ { n } \theta _ {ij} \overline \phi \; _ {i} . $$
Extensions corresponding to boundary value problems.
Extensions of semi-bounded operators play a central role in the theory of elliptic boundary value problems. For example, let $ l ( y) $ be an elliptic differential expression of the second order in a region $ G $ of the $ n $- dimensional space, and let $ A _ {0} $ and $ A = A _ {0} ^ {*} $ be the minimal and maximal operators determined by this expression. Then $ A _ {0} $ is positive definite, its defect numbers are infinite and the defect subspace $ L _ {0} = \mathop{\rm Ker} A $( called the space of $ l $- harmonic functions on $ G $) has a natural realization as a function space on the boundary $ \partial G $ of $ G $. Thus, various extensions of $ A _ {0} $ correspond to various boundary conditions and thus determine various boundary value problems. In particular, the Friedrichs extension $ \widehat{A} _ {0} $ is defined on all functions in the Sobolev space $ W _ {2} ^ {2} ( G) $ that vanish on $ \partial G $, and the equation $ \widehat{A} _ {0} u = f $ corresponds to the Dirichlet problem:
$$ l ( u) = f,\ \ \left . u \right | _ {\partial G } = 0. $$
The theory of partial differential equations gives rise to a number of general questions about extensions of symmetric operators, such as the question of uniqueness of a self-adjoint extension (so-called essential self-adjointness), whether operators that commute (in some sense) have commuting extensions, whether there exist intermediate extensions with given properties (for example, with conditions on the spectrum), etc. (see [7]–[9]).
Extensions into an enlarged Hilbert space.
Every symmetric operator acting on a Hilbert space $ H $ can be extended to a self-adjoint operator acting on some space $ H _ {1} \supset H $( see [10]), and so every symmetric operator has a generalized spectral function. This is related to various results on extensions from a space and on dilatations (see [11]). Thus, any contraction of a Hilbert space (that is, any operator of norm $ \leq 1 $) can be extended to a co-isometric operator (that is, the adjoint of an isometric operator), and every contraction whose powers strongly converge to zero can be extended to a backwards one-sided shift (that is, the adjoint of a one-sided shift). Results about extensions into an enlarged space can be generalized to commutative families, semi-groups, etc.
References
| [1] | N. Dunford, J.T. Schwartz, "Linear operators. Spectral theory" , 2 , Interscience (1963) |
| [2] | M.A. Naimark, "Lineare Differentialoperatoren" , Akademie Verlag (1960) (Translated from Russian) |
| [3] | T. Kato, "Perturbation theory for linear operators" , Springer (1966) pp. Chapt. X Sect. 3 |
| [4a] | M.G. Krein, "Theory of selfadjoint extensions of semibounded Hermitian transformations and its applications I" Mat. Sb. , 20 (1947) pp. 431–498 (In Russian) |
| [4b] | M.G. Krein, "Theory of selfadjoint extensions of semibounded Hermitian transformations and its applications II" Mat. Sb. , 21 (1947) pp. 365–404 (In Russian) |
| [5] | M.Sh. Birman, "On the theory of selfadjoint extensions of positive definite operators" Mat. Sb. , 38 (1956) pp. 431–450 (In Russian) |
| [6] | R.S. Phillips, "Dissipative operators and hyperbolic systems of partial differential equations" Trans. Amer. Math. Soc. , 90 : 2 (1959) pp. 193–254 |
| [7] | K. Moren, "Methods of Hilbert spaces" , PWN (1967) (Translated from Polish) |
| [8] | Yu.M. [Yu.M. Berezanskii] Berezanskiy, "Expansion in eigenfunctions of selfadjoint operators" , Amer. Math. Soc. (1968) (Translated from Russian) |
| [9] | S.G. Mikhlin, "The problem of the minimum of a quadratic functional" , Holden-Day (1965) (Translated from Russian) |
| [10] | M.A. Naimark, "Spectral functions of a symmetric operator" Izv. Akad. Nauk SSSR Ser. Mat. , 4 (1940) pp. 277–318 (In Russian) |
| [11] | B. Szökefalvi-Nagy, Ch. Foiaş, "Harmonic analysis of operators on Hilbert spaces" , North-Holland (1970) (Translated from French) |
| [12] | L. Brown, R. Douglas, P. Fillmore, "Unitary equivalence modulo the compact operators and extensions of 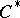 -algebras" , Proc. Conf. Operator Theory , Lect. notes in math. , 345 , Springer (1973) pp. 58–128 -algebras" , Proc. Conf. Operator Theory , Lect. notes in math. , 345 , Springer (1973) pp. 58–128 |
| [13] | W. Arveson, "Notes on extensions of 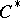 -algebras" Duke Math. J. , 44 : 2 (1977) pp. 329–355 -algebras" Duke Math. J. , 44 : 2 (1977) pp. 329–355 |
| [14] | M. Reed, B. Simon, "Methods of contemporary mathematical physics" , II: Fourier analysis, self-adjointness , Acad. Press (1975) |
Comments
The notation $ \dot{+} $ is another occasionally used notation for the (internal) direct sum $ \oplus $, i.e. $ V = A \dot{+} B $ signifies that $ V = A + B $ and $ A \cap B = \{ 0 \} $.
When dealing with a differential expression
$$ \tag{a1 } l ( y) = \sum _ { i= } 0 ^ { n } ( - 1 ) ^ {n-} i ( p _ {i} ( x) y ^ {(} n- i) ) ^ {(} n- i) $$
it may happen that $ l ( y) $ makes sense even though not all derivatives $ y ^ {(} i) $, $ i = 1 \dots 2 n $, exist; this is connected with possible non-differentiability of the coefficients $ p _ {0} \dots p _ {n} $. One therefore defines the quasi-derivatives $ y ^ {[} 1] \dots y ^ {[} 2n] $ of $ y $ corresponding to the expression (a1) above by the formulas
$$ y ^ {[} k] = \frac{d ^ {k} y }{d x ^ {k} } = \ y ^ {(} k) \ \textrm{ for } k = 1 \dots n - 1 , $$
$$ y ^ {[} n] = p _ {0} y ^ {(} n) , $$
$$ y ^ {[} n+ k] = p _ {k} y ^ {(} n- k) - \frac{d}{dx} ( y ^ {[} n+ k- 1] ) ,\ k = 1 \dots n . $$
In addition one sets $ y ^ {[} 0] = y $. Thus, $ l ( y) = y ^ {[} 2n] $.
There exists another class of problems which go by the name of extension problems. These are matrix extension problems and operator extension problems, in which the matrices (operators) are incompletely given and it is required to "fill-in" the missing "entries" in such a way that the resulting matrix (operator) has certain specified properties. For instance, in one finite version of the Carathéodory–Toeplitz problem one has given a band around the diagonal of an $ ( n \times n) $- matrix $ A $: $ a _ {ij} = a _ {i-} j $, $ | i - j | \leq r < n - 1 $, such that $ a _ {j} = \overline{a}\; _ {-} j $( and some other necessary conditions), and it is required to find the remaining $ a _ {r+} 1 \dots a _ {n-} 1 $ such that the resulting matrix has non-negative definite real part. There is a corresponding infinite version which is important in signal analysis.
Such problems relate to the interpolation of operators.
Extension of an operator. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Extension_of_an_operator&oldid=46883