Euclidean space over a field

Let $F$ be a (commutative) field of characteristic not two. A Euclidean space is a vector space $X$ over $F$ equipped with a symmetric bilinear form $\sigma : X \times X \rightarrow F$ satisfying $\sigma ( x , x ) \neq 0$ for all $x \in X$, $x \neq 0$. The elements of $X$ are called points, and a set of points $p + F . v $ ($p , v \in X$, $v \neq 0$) is called a line. Let $Q ( x ) = \sigma ( x , x )$. Two pairs $( a , b )$, $( c , d )$ of points $a$, $b$, $c$, $d$ are said to be congruent if and only if $Q ( a - b ) = Q ( c - d )$.

Characterization of Euclidean planes.

A fundamental problem is to characterize classes of Euclidean spaces by means of geometric structures, i.e. structures of abstract points and lines equipped with suitable relations on the objects (e.g., of order, congruence, parallelity, continuity). The classical case $F = \mathbf{R}$, $X = \mathbf{R} ^ { 2 }$, $\sigma ( x , y ) = x _ { 1 } y _ { 1 } + x _ { 2 } y _ { 2 }$, as well as some generalizations, were treated by D. Hilbert in [a3] (see also [a1] and [a6]). There are many results concerning the fundamental problem (see [a4]). An example of such a result is Schröder's theorem [a5], which can be described in a fairly elementary way: Let $P$ be a set (no stipulation about the elements of $P$ is made, except that they will be called points). Let $P _ { 2 }$ be the set of all two-element sets $\{ a , b \}$ with $a , b \in P$. Suppose that $\equiv$ is some equivalence relation on $P _ { 2 }$. This structure will be written as $( P , \equiv )$. (Intuitively, $P$ is the real plane and $\{ a , b \} \equiv \{ c , d \}$ means that the segments $a b$ and 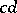are of equal length.) For two distinct points $a$, $b$, the set $l _ { ab }$ of all points $x$ with $\{ a , x \} \equiv \{ b , x \}$ is called a line. Two lines are called parallel if they have no point in common or coincide. Let $L$ be the set of all lines of $( P , \equiv )$. Such a structure is called a Euclidean plane if:

1) The structure $( P , L )$ of points and lines of $( P , \equiv )$ is an affine plane (i.e., for two distinct points there is exactly one line containing them; for a point $p$ and a line $l$ there is exactly one line $g \ni p$ parallel to $l$; and there exist three distinct points not on a common line).

2) Let $a$, $b$, $c$, $d$ be distinct points such that no three of them are collinear (i.e., are on a common line). If the line through $a$ and $b$ is parallel to the line through $c$ and $d$ and the line through $b$ and $c$ is parallel to the line through $a$ and $d$, then $\{ a , b \} \equiv \{ c , d \}$.

3) Let $m$ and $a$ be distinct points. Then there is exactly one point $b$ on the line through $a$ and $m$ such that $m \neq b \neq a$ and $\{ m , a \} \equiv \{ m , b \}$.

An example of a Euclidean plane can be constructed as follows. Let $P$ be the set of nine (distinct) elements $a_1$, $a _2$, $a_3$, $b_{1}$, $b _ { 2 }$, $b _ { 3 }$, $c_1$, $c_2$, $c_{3}$. Two such points are called related if, and only if, the letter of the points or their index are the same. Let $\{ p , q \} \equiv \{ r , s \}$, for points $p$, $q$, $r$, $s$ with $p \neq q$ and $r \neq s$, precisely if the pairs $p$, $q$ and $r$, $s$ of points are both related or both not related.

If $( X , \sigma )$ is a Euclidean space of dimension two over $F$, then $( X , \equiv )$ is a Euclidean plane. Schröder's theorem states that, up to isomorphism, these are the only Euclidean planes.

Historical remarks.

A landmark in the development of the notion of a Euclidean space is the book [a7] by M. Pasch (first published in 1882). In it, Pasch concentrated himself, in an in geometry at that time unusual rigorous manner, on understanding the basic notions of geometry and the relations between them. This was the time for clarifying the notions in mathematics: the notion of a real number was clarified by R. Dedekind in [a8] (first published in 1872).

Pasch was aware of the gap left in the geometry of Euclid: Euclid had tacitly assumed that a line divides the plane in two parts, a fact that is not a consequence of the axioms (see also Euclidean geometry). It led Pasch to the discovery of his famous axioms of order (see Pasch axiom). Note that already C.F. Gauss [a9] noted that the word "between" was not properly defined in mathematics. Pasch now realized that a theory of between-ness was important in the systematic approach to geometry.

Nevertheless, Pasch was thinking of a single geometry, "the" geometry. Of course, there was the problem of the axiom of parallelity (cf. also Fifth postulate; Lobachevskii geometry): Is it true or not in reality? Pasch finished his considerations on the basis of so-called absolute geometry. So, he left his theory open for development in the direction of either Euclidean or non–Euclidean geometry. But, again, it was "the" geometry he was concerned with. In his understanding, geometry was part of natural science.

When D. Hilbert published his book [a3] in 1899, the discipline was no longer part of natural science, but had become a part of pure mathematics. Categorical structures like the real Euclidean plane were, and still are, fundamental. (A structure is called categoric if it is uniquely defined up to isomorphism, i.e. up to the notations of the objects and relations involved.) However, the so-called polymorphic structures became more and more important in geometry. The theory of space geometry gained very much by Hilbert's systematic transition from categorical to polymorphic structures.

Distance spaces.

Of special interest are the Euclidean spaces $( X , \sigma )$ over $\mathbf{R}$ with $\sigma ( x , x ) > 0$ for all $x \in X$ with $x \neq 0$, the so-called pre-Hilbert spaces (cf. also Pre-Hilbert space). Of course, in this case $\sqrt { \sigma ( x , x ) }$ is denoted by $\| x \|$ and $\sigma ( x , y )$ by $x y$. Such Euclidean spaces are the so-called real Euclidean spaces. To be able to present the fundamental geometric objects of these, very important, spaces, the notion of a real distance space is introduced. This is a set $S \neq \emptyset$ together with a mapping $d : S \times S \rightarrow \mathbf R$. Note that for a pre-Hilbert space, $S = X$ and $d ( x , y ) = \| x - y \|$.

Let $( S , d )$ be a real distance space. Its points are the elements of $S$. The real number $d ( x , y )$ is called the distance between $x$ and $y$ (in this order). If $m \in S$ and $\rho \in \mathbf{R}$, the set $S ( m , \rho )$ of all points $x$ with $d ( x , m ) = \rho$ is called the hypersphere with centre at $m$ and radius $\rho$. If $a \neq b$ are points, then the set $g ( a , b )$ of all $x \in S$ such that $S ( a , d ( a , x ) )$ and $S ( b , d ( b , x ) )$ intersect precisely in $x$, is said to be a line. The segment $[ a , b ]$, for points $a \neq b$, is defined by

\begin{equation*} \{ x \in g ( a , b ) : d ( a , x ) \leq d ( a , b ) \geq d ( b , x ) \}. \end{equation*}

A subset $T$ of $S$ is called a linear subspace, respectively a convex set, if $a \neq b$ implies $g ( a , b ) \subseteq T$, respectively $[ a , b ] \subseteq T$, whenever $a , b \in T$. Intersections of hyperspheres $S ( m , \rho )$ with linear subspaces $T \ni m$ are called spherical subspaces of $S$. A mapping $f : S \rightarrow S$ is an isometry of $S$ if $d ( x , y ) = d ( f ( x ) , f ( y ) )$ for all $x$, $y$. Motions are bijective isometries. The set of motions of $S$ is a group, $G$, with respect to the composition product. The image of $S ( m , \rho )$ (respectively, of $g ( a , b )$ and $[ a , b ]$) is $S ( f ( m ) , \rho )$ (respectively, $g ( f ( a ) , f ( b ) )$, $[ f ( a ) , f ( b ) ]$) for $f \in G$. If $p$ and $q$ are distinct points, then the union of the segments $[ p , x ] \ni q$ is called the half-line with starting point $p$. Let $h_{1}$, $h _ { 2 }$ be distinct half-lines with the same starting point, and let $D$ be the intersection of all linear subspaces $T$ of $S$ containing $h _ { 1 } \cup h _ { 2 }$. If $D$ is not a line, then the angle-space $W ^ { + } ( h _ { 1 } , h _ { 2 } , p )$ is the union of all $[ x , y ] \backslash \{ x , y \}$, $x \neq y$, where $x \neq p$ is on $h_{1}$ and $y \neq p$ on $h _ { 2 }$. The set $\{ W ^ { + } \cup h _ { 1 } \cup h _ { 2 } \}$ is the angle-space $W ^ { - } ( h _ { 1 } , h _ { 2 } , p )$. The ordered quadruple $( h _ { 1 } , h _ { 2 } , p , W )$ is called an angle if $W$ is one of the angle-spaces $W ^ { + }$, $W^{-}$. Two angles $( h _ { 1 } , h _ { 2 } , p , W )$ and $( h _ { 1 } ^ { \prime } , h _ { 2 } ^ { \prime } , p ^ { \prime } , W ^ { \prime } )$ are said to be equal if there exists a motion mapping $h_{1}$, $h _ { 2 }$, $p$, $W$ to $h _ { 1 } ^ { \prime }$, $h _ { 2 } ^ { \prime }$, $p ^ { \prime }$, $W ^ { \prime }$, respectively. If $\Gamma$ is the set of all angles $( h _ { 1 } , h _ { 2 } , p , W )$ with $W = W ^ { + }$, then a mapping $\mu$ of $\Gamma$ into the set of all non-negative real numbers is called an angle-measure if:

a) $\Phi _ { 1 } , \Phi _ { 2 } \in \Gamma$ and $\Phi _ { 1 } = \Phi _ { 2 }$ imply $\mu ( \Phi _ { 1 } ) = \mu ( \Phi _ { 2 } )$;

b) if $\Phi = ( h _ { 1 } , h _ { 2 } , p , W ^ { + } )$ is in $\Gamma$ and $h _ { 3 } \subset W ^ { + } \cup \{ p \}$ is a half-line with starting point $p$, then $\mu ( \Phi ) = \mu ( \Phi _ { 1 } ) + \mu ( \Phi _ { 2 } )$ whenever $\Phi _ { 1 } = ( h _ { 1 } , h _ { 3 } , p , W _ { 1 } ^ { + } )$ and $\Phi _ { 2 } = ( h _ { 3 } , h _ { 2 } , p , W _ { 2 } ^ { + } )$ are angles in $\Gamma$ with corresponding angle-spaces $W _ { 1 } ^ { + }$ and $W _ { 2 } ^ { + }$.

For a real Euclidean space with $d ( x , y ) = \| x - y \|$ one obtains the classical notions. For $d ( x , y ) \geq 0$ and $\cosh d ( x , y ) = \sqrt { 1 + x ^ { 2 } } \sqrt { 1 + y ^ { 2 } } - x y$ one obtains the objects of hyperbolic geometry [a2].

References

[a1]	W. Benz, "Grundlagen der Geometrie" Dokumente Geschichte der Math. , 6 (1990) pp. 231–267
[a2]	W. Benz, "Reelle Abstandsräume und hyperbolische Geometrie" Results in Math. , 34 (1998) pp. 56–68
[a3]	D. Hilbert, "Grundlagen der Geometrie" , Teubner (1972)
[a4]	H. Karzel, H.-J. Kroll, "Geschichte der Geometrie seit Hilbert" , Wiss. Buchgesell. Darmstadt (1988)
[a5]	M. Schröder, "Geometrie euklidischer Ebenen" , Schöningh Paderborn (1985)
[a6]	M.M. Toepell, "Uber die Entstehung von David Hilberts Grundlagen der Geometrie" , Vandenhoeck&Ruprecht (1986)
[a7]	M. Pasch, "Vorlesungen über neuere Geometrie" , Teubner (1882)
[a8]	R. Dedekind, "Stetigkeit und irrationale Zahlen" , Braunschweig (1872)
[a9]	C.F. Gauss, "Werke" , VIII , Teubner (1900) pp. 222