Conformal invariants

Let $( M , g )$ be any Riemannian manifold, consisting of a smooth manifold $M$ and a non-degenerate symmetric form $g$ on the tangent bundle of $M$, not necessarily positive-definite. By definition, for any strictly positive smooth function $\lambda : M \rightarrow \mathbf{R} ^ { + }$ the Riemannian manifold $( M , \lambda g )$ is conformally equivalent to $( M , g )$ (cf. also Conformal mapping), and a tensor $T ( g )$ (cf. also Tensor analysis) constructed from $g$ and its covariant derivatives is a conformal invariant if and only if for some fixed weight $k$ the tensor $\lambda ^ { k } T ( \lambda g )$ is independent of $\lambda$. The tensor $g$ is itself a trivial conformal invariant of weight $k = - 1$, and the dimension of $M$ and signature of $g$ can be regarded as trivial conformal invariants, of weight $k = 0$. However, there are many non-trivial conformal invariants of Riemannian manifolds of dimension $n > 2$, and non-trivial scalar conformal invariants have been the subject of much recent work, sketched below. One can also extend the definition to include conformal invariants that are not tensors; these will not be considered below.

An $n$-dimensional Riemannian manifold $( M , g )$ is flat in a neighbourhood $N \subset M$ of a point $P \in M$ if there are coordinate functions $x ^ { 1 } , \ldots , x ^ { p }$, $y ^ { 1 } , \dots , y ^ { q }$ such that

\begin{equation*} g = \{ d x ^ { 1 } \bigotimes d x ^ { 1 } + \ldots + d x ^ { p } \bigotimes d x ^ { p } \} + \end{equation*}

\begin{equation*} - \{ d y ^ { 1 } \bigotimes d y ^ { 1 } + \ldots + d y ^ { q } \bigotimes d y ^ { q } \} \end{equation*}

on $N$, where $p + q = n$ and $p - q$ is the signature of $g$. A manifold is (locally) conformally flat if it is locally conformally equivalent to a flat manifold; the modifier "locally" is a tacit part of the definition, normally omitted. Clearly, conformally flat manifolds have no non-trivial conformal invariants.

For any smooth manifold $M$, let $C ^ { \infty } ( M )$ be the ring of smooth real-valued functions $M \rightarrow \mathbf{R}$ (regarded as an algebra over $\mathbf{R}$), let $\cal E$ be the usual $C ^ { \infty } ( M )$-module of $1$-forms over $M$, and for any $r \geq 0$, let $\otimes ^ { r } \mathcal{E}$ denote the $r$-fold tensor product $\cal E \otimes \ldots \otimes E$ over $C ^ { \infty } ( M )$. In particular, the non-degenerate symmetric form $g$ of a Riemannian manifold will be regarded as a symmetric element of $\otimes ^ { 2 } \mathcal{E}$, as above. The conformal invariance condition $\lambda ^ { k } T ( \lambda g ) = T ( g )$ is entirely local, so that one may as well assume that $M$ is itself an open set in ${\bf R} ^ { n }$. One finds that the signature is of little interest in the construction of conformal invariants, since strategically placed $\pm$ signs turn constructions for the strictly Riemannian case $( p , q ) = ( n , 0 )$ into corresponding constructions for the general case. Hence the existence of conformal invariants depends only on the dimension $n$.

In the next few paragraphs the discussion of conformal invariants is organized by dimension $n$; at the end the discussion centres exclusively on recent work concerning scalar conformal invariants for the cases $n \geq 4$.

Dimension one.

Any $1$-dimensional Riemannian manifold $( M , g )$ is trivially conformally flat, so that there are no non-trivial conformal invariants in dimension $n = 1$.

Dimension two.

If $( M , g )$ is a Riemannian manifold of dimension $n = 2$, let

\begin{equation*} g = E d x \bigotimes d x + \end{equation*}

\begin{equation*} + F ( d x \bigotimes d y + d y \bigotimes d x ) + G d y \bigotimes d y \end{equation*}

in some neighbourhood of any point $P \in M$. The question of conformal flatness of $( M , g )$ breaks into two cases, as follows.

i) If $E G - F ^ { 2 } < 0$ the usual method of factoring $E s ^ { 2 } + 2 F s t + G t ^ { 2 } \in C ^ { \infty } ( M ) [ s , t ]$ into a product of two linear homogeneous factors leads to a product $\theta \otimes \varphi \in \otimes ^ { 2 } \mathcal{E}$ of linearly independent $1$-forms, whose symmetric part is $g = ( \theta \otimes \varphi + \varphi \otimes \theta ) / 2$. Since $n = 2$, there are smooth functions $\lambda$, $\mu$, $\rho$, $\sigma$ in a neighbourhood of $P$ such that $\theta = \lambda d \rho$ and $\varphi = \mu d \sigma$, so that $g = \lambda \mu ( d \rho \otimes d \sigma + d \sigma \otimes d \rho ) / 2$. By setting $\rho = u + v$ and $\sigma = u - v$, one then has $g = \lambda \mu ( d u \otimes d u - d v \otimes d v )$ in a neighbourhood of $P$; hence $( M , g )$ is conformally flat.

ii) The case $E G - F ^ { 2 } > 0$ is the classical problem of finding isothermal coordinates for a Riemann surface, first solved by C.F. Gauss in a more restricted setting. More recent treatments of the same problem are given in [a9], [a10], [a4]; these results are easily adapted to the smooth case to show that any (smooth) Riemannian surface $( M , g )$ with a positive-definite (or negative-definite) metric $g$ is conformally flat. It follows from i) and ii) that there are no non-trivial conformal invariants in dimension $n = 2$.

Dimension at least three.

Some classical conformal invariants in dimensions $n \geq 3$ are as follows (their constructions will be sketched later):

In 1899, E. Cotton [a7] assigned a tensor $C ( g ) \in \otimes ^ { 3 } \mathcal{E}$ to any Riemannian manifold $( M , g )$ of any dimension $n \geq 3$; it is conformally invariant of weight $k = 0$ only in the special case $n = 3$, and J.A. Schouten [a12] showed that in this case $( M , g )$ is conformally flat if and only if $C ( g ) = 0$.

In 1918, H. Weyl [a14] constructed a tensor $W ( g ) \in \otimes ^ { 4 } \mathcal{E}$ for any Riemannian manifold $( M , g )$ of dimension $n \geq 3$, conformally invariant of weight $k = - 1$ for all dimensions $n \geq 3$ although it vanishes identically for $n = 3$. Schouten [a12] showed that a Riemannian manifold $( M , g )$ of dimension $n \geq 4$ is conformally flat if and only if $W ( g ) = 0$, and $W ( g )$ is now known as the Weyl curvature tensor (cf. also Weyl tensor).

The remaining classical tensor $B ( g ) \in \otimes ^ { 2 } \mathcal{E}$ was constructed by R. Bach [a1] in 1921; although $B ( g )$ exists in any dimension $n \geq 3$, it is conformally invariant, of weight $k = 1$, only for Riemannian manifolds $( M , g )$ of dimension $n = 4$, and in this dimension $B ( g ) = 0$ if and only if $( M , g )$ is conformally equivalent to an Einstein manifold (see below).

Algebraic background.

The primarily algebraic background needed to describe these three classical conformal invariants is also needed to sketch the more recent construction of the scalar conformal invariants, mentioned earlier. Let $\mathcal{R}$ be any commutative ring with unit that is also an algebra over the real numbers; the ring $\mathcal{R}$ will later be $C ^ { \infty } ( M )$ for a smooth manifold $M$. Let $\cal E$ be an $\mathcal{R}$-module, let $\cal E_{*} = \operatorname { Hom } _ { R } ( E , R )$, let $\mathcal{E}_{ * *} = \operatorname { Hom } _ { \mathcal{R} } ( \mathcal{E}_ * , \mathcal{R} )$, and assume that the natural homomorphism from $\cal E$ to its double dual $\mathcal{E}_{ * *}$ is an isomorphism ${\cal E} \overset{\approx}{\to} {\cal E} _ {* * }$; the $\mathcal{R}$-module $\cal E$ will later be the $C ^ { \infty } ( M )$-module of $1$-forms on $M$, and $\mathcal{E} _ { * }$ will be the $C ^ { \infty } ( M )$-module of smooth vector fields on $M$. As before, for any $r \geq 0$ let $\otimes ^ { r } \mathcal{E}$ denote the $r$-fold tensor product over $\mathcal{R}$, later the $C ^ { \infty } ( M )$-module of contravariant tensors of degree $r$ over $M$.

If $\tau _ { 2 } : \otimes ^ { 2 } \mathcal{E} \rightarrow \otimes ^ { 2 } \mathcal{E}$ is the $\mathcal{R}$-module isomorphism that interchanges the two factors $\cal E$, an element $g \in \otimes ^ { 2 } \mathcal{E}$ is symmetric if $\tau _ { 2 } g = g$. Let $\mathsf{S} ^ { 2 } \mathcal{E} \subset \otimes ^ { 2 } \mathcal{E}$ be the submodule of symmetric elements; it consists of $\mathcal{R}$-linear combinations of products of the form $\theta \otimes \theta \in \mathsf{S} ^ { 2 } \mathcal{E}$. One can regard any $g \in \mathsf{S} ^ { 2 } \cal E$ as a homomorphism $g : \otimes ^ { 2 } \cal E * \rightarrow R$, so that there is an induced homomorphism 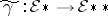such that $\langle \tilde { \gamma } ( X ) , Y \rangle = g ( X \otimes Y ) \in \mathcal{R}$ for any $X \otimes Y \in \otimes ^ { 2 } \cal E_{*}$. The isomorphism ${\cal E} \overset{\approx}{\to} {\cal E} _ {* * }$ permits one to regard $\tilde{\gamma}$ as a homomorphism $\gamma : \mathcal{E}_{*} \rightarrow \mathcal{E}$, and $g$ is non-degenerate if $\gamma$ is an isomorphism. In this case the inverse $\gamma ^ { - 1 } : \cal E \rightarrow E *$ provides a unique element $g ^ { - 1 } \in \mathsf{S} ^ { 2 } \cal E _{*}$ that can be regarded as a homomorphism $g ^ { - 1 } : \otimes ^ { 2 } \mathcal{E} \rightarrow \mathcal{R}$ with values $g ^ { - 1 } ( \theta \otimes \varphi ) = \langle \theta , \gamma ^ { - 1 } ( \varphi ) \rangle \in \mathcal R $ for any $\theta \otimes \varphi \in \otimes ^ { 2 } \mathcal{E}$. One easily verifies that $g ^ { - 1 }$ is itself non-degenerate.

For any $r \geq 0$, let $\{ p , q \}$ be an unordered pair of distinct elements in $\{ 1 , \dots , r , r + 1 , r + 2 \}$ and let $g \in \mathsf{S} ^ { 2 } \cal E$ be non-degenerate. Then one can evaluate $g ^ { - 1 }$ on the tensor product $\mathcal{E} \otimes \mathcal{E}$ of the $p$th and $q$th factors of $\otimes ^ { r + 2 } \mathcal{E}$ to obtain a well-defined $\mathcal{R}$-linear contraction $g ^ { - 1 } \{ p , q \} : \otimes ^ { r + 2 } \mathcal{E} \rightarrow \otimes ^ { r } \mathcal{E}$. The symmetry of $g ^ { - 1 }$ guarantees that $g ^ { - 1 } \{ p , q \}$ does not require an ordering of $\{ p , q \}$. Similarly, if $\{ p , q , r , s \}$ is any unordered subset of $\{ 1 , \ldots , r , r + 1 , \ldots , r + 4 \}$, there is a well-defined $\mathcal{R}$-linear contraction $g ^ { - 1 } \{ p , q ; r , s \} : \otimes ^ { r + 4 } \mathcal{E} \rightarrow \otimes ^ { r } \mathcal{E}$, where $g ^ { - 1 } \{ p , q , r , s \} = g ^ { - 1 } \{ p , q \} g ^ { - 1 } \{ r , s \} = g ^ { - 1 } \{ r , s \} g ^ { - 1 } \{ p , q \}$.

An element $\Theta \in \otimes ^ { 2 } \mathcal{E}$ is alternating if $\tau _ { 2 } \Theta = - \Theta$, and there is a submodule $\mathsf{A} ^ { 2 } \mathcal{E} \subset \otimes ^ { 2 } \mathcal{E}$ that consists of all such alternating elements. If $\mathcal{R}$ is the ring $C ^ { \infty } ( M )$ for a Riemannian manifold $( M , g )$, and if $\cal E$ is the $\mathcal{R}$-module of $1$-forms on $M$, then the classical Riemannian curvature tensor of $( M , g )$ (cf. also Curvature tensor; Riemann tensor) is a symmetric element $R ( g ) \in \mathsf{A} ^ { 2 } \mathcal{E} \otimes \mathsf{A} ^ { 2 } \mathcal{E}$, for the submodule $\mathsf{A} ^ { 2 } \mathcal{E} \otimes \mathsf{A} ^ { 2 } \mathcal{E} \subset \otimes ^ { 4 } \mathcal{E}$; a construction is sketched below. The corresponding Ricci curvature is the contraction $\operatorname { Ric } ( g ) = g ^ { - 1 } \{ 2,3 \} R ( g ) = g ^ { - 1 } \{ 1,4 \} R ( g ) \in \mathsf{S} ^ { 2 } \mathcal{E}$, and the corresponding scalar curvature is the contraction $S ( g ) = g ^ { - 1 } \{ 1,2 \} \operatorname { Ric } ( g ) = g ^ { - 1 } \{ 1,4 ; 2,3 \} R ( g ) \in C ^ { \infty } ( M )$. In case $M$ is of dimension $n \geq 3$, there is a nameless tensor

\begin{equation*} A ( g ) = \frac { 1 } { n - 2 } \left( \operatorname { Ric } ( g ) - \frac { 1 } { 2 } \frac { S ( g ) } { n - 1 } g \right) \in \mathsf{S} ^ { 2 } \cal E \end{equation*}

that is used to construct all three classical conformal invariants.

The construction of the Weyl curvature tensor $W ( g ) \in \mathsf{A} ^ { 2 } \mathcal{E} \otimes \mathsf{A} ^ { 2 } \mathcal{E}$ uses a $C ^ { \infty } ( M )$-module homomorphism from the submodule $\mathsf{S} ^ { 2 } \mathcal{E} \otimes \mathsf{S} ^ { 2 } \mathcal{E} \subset \bigotimes ^ { 4 } \mathcal{E}$ to the submodule of symmetric elements in $\mathsf{A} ^ { 2 } \mathcal{E} \otimes \mathsf{A} ^ { 2 } \mathcal{E} \subset \otimes ^ { 4 } \mathcal{E}$. If $0 < p \leq 4$, let $\tau _ { p } : \otimes ^ { 4 } \mathcal{E} \rightarrow \otimes ^ { 4 } \mathcal{E}$ be the isomorphism that permutes the $p$th factor $\cal E$ in $\otimes ^ { 4 } \mathcal{E}$ to the left of the first $p - 1$ factors $\cal E$ in $\otimes ^ { 4 } \mathcal{E}$, so that $\tau _ { p }$ is cyclic in the usual sense that $\tau ^ { p_p } = 1$, and $\tau ^ { - 1 } p$ simply places the first factor into the $p$th slot; in particular, $\tau_1$ is the identity, and $\tau_2$ interchanges the first two factors as before. For any $h \otimes k \in \mathsf{S} ^ { 2 } \mathcal{E} \otimes \mathsf{S} ^ { 2 } \mathcal{E}$, set

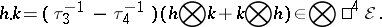By looking at the special cases $h \otimes k = ( \theta \otimes \theta ) \otimes ( \varphi \otimes \varphi ) \in \mathsf{S} ^ { 2 } \mathcal{E} \otimes \mathsf{S} ^ { 2 } \mathcal{E}$, for any $\theta \in \mathcal{E}$ and $\varphi \in \mathcal{E}$, one obtains

\begin{equation*} h . k = ( \theta \bigotimes \varphi - \varphi \bigotimes \theta ) \bigotimes ( \theta \bigotimes \varphi - \varphi \bigotimes \theta ) \in \end{equation*}

\begin{equation*} \in \mathsf{A} ^ { 2 } {\cal E} \bigotimes \mathsf{A} ^ { 2 } {\cal E}; \end{equation*}

these cases induce the announced homomorphism $\mathsf{S} ^ { 2 } \mathcal{E} \otimes \mathsf{S} ^ { 2 } \mathcal{E} \rightarrow \mathsf{A} ^ { 2 } \mathcal{E} \otimes \mathsf{A} ^ { 2 } \mathcal{E}$.

For any Riemannian manifold $( M , g )$ of dimension $n \geq 3$, the Weyl curvature tensor is the difference $W ( g ) = R ( g ) - g \cdot A ( g ) \in \mathsf{A} ^ { 2 } \mathcal{E} \otimes \mathsf{A} ^ { 2 } \mathcal{E} $, which is a non-trivial conformal invariant of weight $k = - 1$ whenever $n \geq 4$. Although the principal feature of $W ( g )$ is that $W ( g ) = 0$ if and only if the Riemannian manifold $( M , g )$ of dimension $n \geq 4$ is conformally flat, it also provides a basic tool for constructing other conformal invariants for manifolds of dimensions $n \geq 4$. For example, for any $m > 0$, let $W ( g ) \otimes \ldots \otimes W ( g ) \in \otimes ^ { 4 m } \mathcal{E}$ be the tensor product of $m$ copies of $W ( g )$, and let $\{ p _ { 1 } , \dots , p _ { 4 m } \} = \{ 1 , \dots , 4 m \}$ as unordered sets. Then the contraction

\begin{equation*} g ^ { - 1 } \{ p _ { 1 } , p _ { 2 } ; \ldots ; p _ { 4 m - 1 } , p _ { 4 m } \} ( W ( g ) \bigotimes \ldots \bigotimes W ( g ) ) \end{equation*}

is a non-trivial scalar conformal invariant $\operatorname{contr}( W ( g ) \otimes \ldots \otimes W ( g ) ) \in C ^ { \infty } ( M )$ of weight $ k = + m$ for any Riemannian manifold $( M , g )$ of dimension $n \geq 4$.

The curvatures $R ( g )$, $\operatorname { Ric } ( g )$, $S ( g )$, and the tensor $A ( g )$ assigned to any Riemannian manifold $( M , g )$ are all constructed via the Levi-Civita connection associated to $g$, defined below, so that $W ( g ) \in \otimes ^ { 4 } \mathcal{E}$ depends implicitly upon the Levi-Civita connection. The remaining classical conformal invariants $C ( g ) \in \otimes ^ { 3 } \mathcal{E}$ and $B ( g ) \in \otimes ^ { 2 } \mathcal{E}$, for Riemannian manifolds of dimensions $n = 3$ and $n = 4$, respectively, as well as most of the scalar conformal invariants that will be introduced below, will be constructed explicitly via a version of the Levi-Civita connection that is sketched in the next two paragraphs; more details of this version appear in [a11].

Levi-Civita connection.

For any smooth manifold $M$ with $C ^ { \infty } ( M )$-module $\cal E$ of $1$-forms as before, a connection (cf. also Connections on a manifold) is a sequence of real linear homomorphisms $\nabla : \otimes ^ { r } \mathcal{E} \rightarrow \otimes ^ { r+ 1 } \mathcal{E}$ such that the complex $\{ \otimes ^ { * } {\cal E} , \nabla \}$ covers the classical de Rham complex $\{ \wedge ^ { * } \mathcal{E} , d \}$ (cf. also Differential form); that is, the diagram

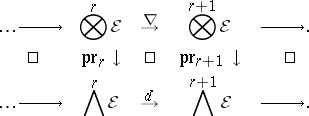commutes for the usual projections 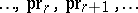from tensor products to exterior products over $C ^ { \infty } ( M )$, where $\wedge ^ { * } \mathcal{E}$ is the quotient of $\otimes ^ { * } \mathcal E$ by the two-sided ideal generated by $\mathsf{S} ^ { 2 } \cal E \subset \otimes ^ { * } E$. Furthermore, if $0 \leq p \leq r$ and if $\tau _ { p + 1 } : \otimes ^ { p + q + 1 } \mathcal{E} \rightarrow \otimes ^ { p + q + 1 } \mathcal{E}$ is the permutation with parity $( - 1 ) ^ { p } \in \{ - 1 , + 1 \}$ that moves the $( p + 1 )$st factor $\cal E$ to the left of the first $p$ factors $\cal E$, then

\begin{equation*} \nabla ( \Theta \bigotimes \Phi ) = \nabla \Theta \bigotimes \Phi + \tau _ { p + 1 } ( \Theta \bigotimes \nabla \Phi ) \in \end{equation*}

\begin{equation*} \in \bigotimes \square ^ { p + q + 1 } \mathcal{E} \end{equation*}

for any $\in \otimes ^ { p } \mathcal{E}$ and $\Phi \in \otimes ^ { q} \mathcal{E}$; the product rule is

\begin{equation*} \nabla ( a \Phi ) = d a \bigotimes \Phi + a \nabla \Phi \in \bigotimes \square ^ { q + 1 } \mathcal{E} \end{equation*}

for $a \in C ^ { \infty } ( M )$. It follows that the covering $\{ \otimes ^ { * } {\cal E} , \nabla \}$ of $\{ \wedge ^ { * } \mathcal{E} , d \}$ also preserves products. If $( M , g )$ is a Riemannian manifold, with metric $g \in \mathsf{S} ^ { 2 } \cal E$ as usual, there is a unique connection $\{ \otimes ^ { * } {\cal E} , \nabla \}$ such that $\nabla g = 0 \in \otimes ^ { 3 } \mathcal{E}$; this is the Levi-Civita connection associated to $( M , g )$ (cf. also Levi-Civita connection).

One useful property of any connection $\{ \otimes ^ { * } {\cal E} , \nabla \}$ for any smooth manifold $M$ is that for any $r \geq 0$ the composition

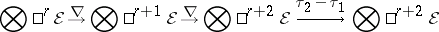is $C ^ { \infty } ( M )$-linear, where $\tau_2$ interchanges the first two factors $\cal E$ of $\otimes ^ { r + 2 } \mathcal{E}$ and $\tau_1$ is the identity isomorphism; for any $r \geq 0$ the homomorphism $( \tau _ { 2 } - \tau _ { 1 } ) \circ \nabla \circ \nabla$ is the curvature operator $R ( \nabla ) : \otimes ^ { r } {\cal E} \rightarrow \otimes ^ {r + 2 } {\cal E}, $. In particular, for any Riemannian manifold $( M , g )$ and corresponding Levi-Civita connection, the tensor product of $R ( \nabla ) : \mathcal{E} \rightarrow \otimes ^ { 3 } \mathcal{E}$ and the identity isomorphism $1 : \mathcal{E} \rightarrow \mathcal{E}$ restricts to a $C ^ { \infty } ( M )$-linear mapping $R ( \nabla ) \otimes {\bf 1} : \mathsf{S} ^ { 2 } {\cal E} \rightarrow \otimes ^ { 4 } {\cal E}$, and the image $( R ( \nabla ) \otimes 1 ) g \in \otimes ^ { 4 } \mathcal{E}$ of the metric $g \in \mathsf{S} ^ { 2 } \cal E$ itself is the Riemannian curvature tensor $R ( g )$, lying in the submodule $\mathsf{A} ^ { 2 } \mathcal{E} \otimes \mathsf{A} ^ { 2 } \mathcal{E} \subset \otimes ^ { 4 } \mathcal{E}$.

Even though the Levi-Civita connection $\{ \otimes ^ { * } {\cal E} , \nabla \}$ of a Riemannian manifold $( M , g )$ is defined in part by the requirement that $\nabla g = 0 \in \otimes ^ { 3 } \mathcal{E}$ for the Riemannian metric $g \in \mathsf{S} ^ { 2 } \cal E$, observe that the definition $R ( g ) = ( R ( \nabla ) \otimes 1 ) g$ of the Riemannian curvature is obtained by applying the curvature operator $( \tau _ { 2 } - \tau _ { 1 } ) \circ \nabla \circ \nabla$ only to the first factor of $g$. Consequently, $R ( g )$, $\operatorname { Ric } ( g )$, $S ( g )$, and $A ( g )$ all require the first two derivatives of $g$, in the obvious sense. The same remark applies to the Weyl curvature tensor $W ( g ) = R ( g ) - g \cdot A ( g ) \in \mathsf{A} ^ { 2 } \mathcal{E} \otimes \mathsf{A} ^ { 2 } \mathcal{E} $.

Cotton tensor.

Let $( M , g )$ be any Riemannian manifold of dimension $n \geq 3$, with $A ( g ) \in \mathsf{S} ^ { 2 } \mathcal{E}$ as before, let

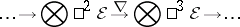be the Levi-Civita connection, which restricts to $\mathsf{S} ^ { 2 } \mathcal{E} \subset \otimes ^ { 2 } \mathcal{E}$, and let $\tau _ { 3 } : \otimes ^ { 3 } {\cal E} \rightarrow \otimes ^ { 3 } {\cal E}$ be the cyclic permutation of the factors $\cal E$ that moves the third factor $\cal E$ to the left of the first two factors $\cal E$. The Cotton tensor is

\begin{equation*} C ( g ) = \nabla A ( g ) - \tau ^ { - 1_3 } \nabla A ( g ) \in \bigotimes \square ^ { 3 } \mathcal{E}, \end{equation*}

which visibly depends on third derivatives of $g$; this is equivalent to the original definition of E. Cotton [a7], and it has the evident cyclic symmetry $C ( g ) + \tau _ { 3 } C ( g ) + \tau ^ { 2_3} C ( g ) = 0$. Furthermore, $C ( g )$ is a conformal invariant if $M$ is of dimension $n = 3$, and Schouten [a12] showed in this case that $C ( g ) = 0 \in \otimes ^ { 3 } \mathcal{E}$ if and only if $( M , g )$ is conformally flat, as noted earlier.

Closed oriented $3$-dimensional Riemannian manifolds.

If one considers closed oriented $3$-dimensional Riemannian manifolds $( M , g )$, the Chern–Simons invariant $\Phi \{ M , g \} \in S ^ { 1 } ( = \mathbf{R} / \mathbf{Z} )$ is shown in [a6] to depend only on the conformal equivalence class $\{ M , g \}$ of $( M , g )$, and $\Phi \{ M , g \} \in S ^ { 1 }$ is a critical value if and only if $\{ M , g \}$ is conformally flat. S.S. Chern [a5] gave a simplified proof of this result by using the criterion $C ( g ) = 0$ of the preceding paragraph.

Bach tensor.

For any Riemannian manifold $( M , g )$ of dimension $n \geq 3$, the Bach tensor is

\begin{equation*} B ( g ) = \end{equation*}

\begin{equation*} = g ^ { - 1 } \{ 1,4 \} \nabla C ( g ) - g ^ { - 1 } \{ 1,3 ; 2,5 \} ( A ( g ) \bigotimes W ( g ) ) \subset \subset \bigotimes \square ^ { 2 } \mathcal{E}, \end{equation*}

for the Levi-Civita connection

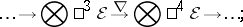one easily verifies that the Bach tensor is an element of $\mathsf{S} ^ { 2 } \mathcal{E} \subset \otimes ^ { 2 } \mathcal{E}$. It is conformally invariant only in the special case $n = 4$, and in that case one has $B ( g ) = 0$ if and only if $( M , g )$ is conformally equivalent to a Riemannian manifold $( \widetilde { M } , \widetilde{g} )$ such that the Ricci curvature $\operatorname{Ric}( \tilde{g} ) \in \mathsf{S} ^ { 2 } \tilde {\cal E }$ is a constant multiple of the metric $\tilde{g} \in \mathsf{S} ^ { 2 } \mathcal{E}$ itself. Riemannian manifolds with the latter property are known as Einstein manifolds.

Recall that for any $m > 0$ the contractions

\begin{equation*} \text{ contr } ( W ( g ) \bigotimes \ldots \bigotimes W ( g ) ) = \end{equation*}

\begin{equation*} = g ^ { - 1 } \{ p _ { 1 } , p _ { 2 } ; \ldots ; p _ { 4 m - 1 } , p _ { 4 m } \} ( W ( g ) \bigotimes \ldots \bigotimes W ( g ) ) \in \in C ^ { \infty } ( M ) \end{equation*}

of the $m$-fold tensor product of the Weyl curvature tensor $W ( g ) \in \mathsf{A} ^ { 2 } \mathcal{E} \otimes \mathsf{A} ^ { 2 } \mathcal{E}$ are scalar conformal invariants of weight $k = m$, and observe that any $C ^ { \infty } ( M )$-linear combination of such contractions is also a scalar conformal invariant of weight $k = m$. Such scalar conformal invariants involve the Riemannian metric $g$ and its first and second order derivatives. However, the derivative 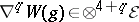is not itself conformally invariant if $q > 0$, so that in general one cannot expect contractions of products 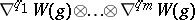to produce conformal invariants if $q_ 1 + \ldots + q_ m > 0$. The following observations suggest a reasonable modification of the construction.

First, observe that if $( M , g )$ and $( \widetilde { M } , \widetilde{g} )$ are Riemannian manifolds for which there is an embedding $M \subset \tilde { M }$ with $\tilde { g } | _ { M } = g$, then any scalar conformal invariant of $( \widetilde { M } , \widetilde{g} )$ restricts to the corresponding scalar conformal invariant of $( M , g )$. Since the construction of conformal invariants is an entirely local question, it suffices to consider embeddings of open sets $M \subset {\bf R} ^ { n }$ into open sets $\tilde { M } \subset \mathbf{R} ^ { n } \times ( 0 , \infty ) \times ( - 1 , + 1 )$, for example. The hypotheses can be weakened if the conformal equivalence class of $( M , g )$ has a real-analytic representative with coordinates $x = ( x _ { 1 } , \ldots , x _ { n } )$. One can then assign a coordinate $t \in ( 0 , \infty )$ and use power series about $r = 0 \in ( - 1 , + 1 )$ to describe the Riemannian metric $\tilde { g }$ of an embedding, knowing that only the restrictions of the derivatives 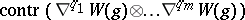to the submanifold $M \subset \tilde { M }$ are of any interest, the inclusion being

\begin{equation*} M \times \{ 1 \} \times \{ 0 \} \subset M \times ( 0 , \infty ) \times ( - 1 + 1 ). \end{equation*}

The second observation is a classical result, not directly related to conformal invariants. Given any Riemannian manifold $( \widetilde { M } , \widetilde{g} )$, with Levi-Civita connection $\{ \otimes ^ { * } \tilde { \mathcal{E} } , \tilde { \nabla } \}$ and Riemannian curvature $R (\tilde{ g} )$, if $q _ { 1 } + \ldots + q _ { m }$ is an even number, then the contractions $\operatorname {contr} ( \tilde { \nabla } ^ { q _ { 1 } } R ( \tilde{g} ) \otimes \ldots \otimes \tilde { \nabla } ^ { q _ { m } } R ( \tilde{g} ) )$ involve derivatives of $\tilde { g }$ of order up to $\operatorname { max } \{ q _ { 1 } + 2 , \ldots , q _ { m } + 2 \}$; furthermore, such contractions are visibly coordinate-free. Results in [a15] imply that if $( M , g )$ is locally real-analytic, then any coordinate-free polynomial combination of $\operatorname { det } \tilde{g} ^ { - 1 }$ and the components of the derivatives $\tilde { \nabla } ^ { q } R ( \tilde { g } )$ is a $C ^ { \infty } ( \widetilde { M } )$-linear combination of such contractions, which are known as Weyl invariants.

The third observation is that if $( \widetilde { M } , \widetilde{g} )$ is a Ricci-flat Riemannian manifold, in the sense that $\operatorname { Ric } ( \tilde{g} ) = 0 \in \mathsf{S} ^ { 2 } \tilde{\mathcal{E}}$, then $S ( \widetilde{g} ) = 0 \in C ^ { \infty } ( \widetilde { M } )$ so that $A ( \tilde{g} ) = 0 \in \mathsf{S} ^ { 2 } \tilde{\mathcal{E}}$; in this case the Riemannian curvature tensor itself is a classical conformal invariant: $R ( \tilde{ g } ) = W ( \tilde { g } ) \in \mathsf{A} ^ { 2 } \mathcal{E} \otimes \mathsf{A} ^ { 2 } \mathcal{E}$. Even though one cannot expect the derivatives $\tilde { \nabla } ^ { q } W ( \tilde { g } )$ nor contractions of products of such derivatives to be conformal invariants, the identifications 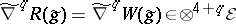suggest that the contractions 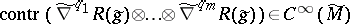may be of value in the Ricci-flat case, whenever $q _ { 1 } + \ldots + q _ { m }$ is an even number.

General construction of scalar conformal invariants.

The preceding observations lead to a general construction of scalar conformal invariants of $( M , g )$, with a dimensional restriction that will be specified later. One first covers $M$ by sufficiently small coordinate neighbourhoods $N$ and writes $( N , g )$ for each resulting Riemannian manifold $( N , g | _ { N } )$. For each $( N , g )$ C. Fefferman and C.R. Graham [a8] use a technique that appeared independently in [a13] to introduce a codimension-$2$ embedding $N \subset \tilde { N }$, described later, and to devise a Cauchy problem whose solution provides a Ricci-flat manifold $( \widetilde { N } , \widetilde{g} )$ with $\tilde { g } | _ { N } = g$. A further feature of the construction guarantees that any Weyl invariant in $C ^ { \infty } ( \tilde { N } )$ restricts to a conformal invariant of $( N , g )$, of weight $k = m + ( q _ { 1 } + \ldots + q _ { m } ) / 2$. Since $C ^ { \infty } ( N )$-linear combinations of scalar conformal invariants of weight $k$ are also scalar conformal invariants of weight $k$, for any fixed $m$-tuple $( q _ { 1 } , \dots , q _ { m } )$ of non-negative integers with an even sum one can use a smooth partition of unity subordinate to the covering of $M$ by the coordinate neighbourhoods $N$ to obtain a scalar conformal invariant of $( M , g )$ itself, known as a Weyl conformal invariant.

T.N. Bailey, M.G. Eastwood and Graham [a2] completed the proof of the following Fefferman–Graham conjecture [a8], which depends upon the parity of $n = \operatorname { dim } M$: If $( M , g )$ is a Riemannian manifold of odd dimension $n$, then every scalar conformal invariant of $( M , g )$ is a Weyl conformal invariant. If $( M , g )$ is a Riemannian manifold of even dimension $n$, then the preceding statement is true only for scalar conformal invariants of weight $k < n / 2$, and there is a conformally invariant element in $\mathsf{S} ^ { 2 } \mathcal{E}$ of weight $k = - 1 + n / 2$ that serves as an obstruction to finding a formal power series solution of the Cauchy problems used to construct the ambient manifolds $( \widetilde { N } , \widetilde{g} )$; the obstruction vanishes if $( M , g )$ is conformally equivalent to an Einstein manifold; if $n = 4$ the obstruction is the Bach conformal invariant $B ( g )$.

There are some exceptional scalar conformal invariants for even dimensions $n$ and weight $k \geq n / 2$, first observed in [a2]; the catalogue of all such exceptional invariants was completed in [a3].

Fefferman–Graham method.

This method, introduced in [a8], allows one to construct the codimension-$2$ embeddings $N \subset \tilde { N }$ of the Riemannian manifolds $( N , g )$, and to formulate the Cauchy problems whose solutions turn each ambient space $\widetilde { N } = N \times ( 0 , \infty ) \times ( - 1 , + 1 )$ into a Ricci-flat manifold $( \widetilde { N } , \widetilde{g} )$ with the desired properties.

One starts with the fibration over $N$ in which the fibre over each $P \in N$ consists of positive multiples $t ^ { 2 } g ( P )$ of the metric $g ( P )$ at $P$; one may as well suppose that $t > 0$. The multiplicative group $\mathbf{R} ^ { + } = ( 0 , \infty )$ of real numbers $s > 0$ acts on the fibres by mapping $t ^ { 2 } g ( P )$ into $s ^ { 2 } t ^ { 2 } g ( P )$, and this permits one to regard the fibration as a fibre bundle with structure group $\mathbf{R} ^ { + }$ (cf. also Principal fibre bundle). Clearly, any section of the fibre bundle can be regarded as a Riemannian manifold that is conformally equivalent to $( N , g )$.

Let $\pi _ { 0 } : N _ { 0 } \rightarrow N$ be the corresponding principal fibre bundle, and observe that since $\operatorname { dim } N _ { 0 } = \operatorname { dim } N + 1$, the pullback $\pi ^ { * _ { 0 }} g \in \mathsf{S} ^ { 2 } {\cal E} _ { 0 }$ of the metric $g \in \mathsf{S} ^ { 2 } \cal E$ over $N$ needs at least one additional term to serve as a Riemannian metric over $N_ 0 $. It is useful to replace $\pi _ { 0 } : N _ { 0 } \rightarrow N$ by another $\mathbf{R} ^ { + }$-bundle $\widetilde{\pi} : \widetilde{N} \rightarrow N$ with $\widetilde { N } = N _ { 0 } \times ( - 1 , + 1 )$, and to try to construct a (non-degenerate) metric $\tilde{g} \in \mathsf{S} ^ { 2 } \tilde{\cal E}$ on $\tilde { N }$ such that

1) the restriction $\tilde{g} | _ { N _ { 0 } \times \{ 0 \}}$ is $\pi _ { 0 } ^ { * } \tilde{g}$;

2) the group elements $s \in \mathbf{R} ^ { + }$ map $\tilde{g} \in \mathsf{S} ^ { 2 } \tilde{\cal E}$ into $s ^ { 2 } \tilde { g } \in \mathsf{S} ^ { 2 } \tilde{\mathcal{E}}$ over all of $\tilde { N }$;

3) $( \widetilde { N } , \widetilde{g} )$ is Ricci-flat, with the consequence $W ( \tilde { g } ) = R ( \tilde { g } ) \in \mathsf{A} ^ { 2 } \tilde{\mathcal{E}} \otimes \mathsf{A} ^ { 2 } \tilde{\mathcal{E}}$ noted earlier. There is an implicit additional assumption, that the conformal equivalence class containing $( N , g )$ is real-analytic in the sense that there is a representative $( N , \lambda g )$ of the conformal class of $( N , g )$ for which one can choose coordinates $x = ( x ^ { 1 } , \dots , x ^ { n } )$ in $C ^ { \infty } ( N )$ such that $\lambda g = \sum _ { i ,\, j } \lambda g_ { i j } d x ^ { i } \otimes d x ^ { j } \in \mathsf{S} ^ { 2 } \mathcal{E}$, for coefficients $\lambda g_{ij} \in C ^ { \infty } ( N )$ that are real-analytic functions of $x$; one may as well assume that $( N , g )$ itself has this property.

The Fefferman–Graham method [a8] leads to a metric of the form

\begin{equation*} \tilde { g } = t ^ { 2 } \sum _ { i ,\, j } \tilde { g } _ { i j } ( x , t ) d x ^ { i } \bigotimes d x ^ { j } + \end{equation*}

\begin{equation*} + 2 r d t \bigotimes d t + t d t \bigotimes d r + t d r \bigotimes d t \end{equation*}

that satisfies 1)–3) for all $( x , t , r ) \in N \times ( 0 , \infty ) \times ( - 1 , + 1 )$ ($= \widetilde { N }$), for real-analytic functions $\tilde{g} _ { i j }$ of $( x , r )$ that satisfy the initial condition 1), $\tilde{g} _ { i j } ( x , 0 ) = g _ { i j } ( x )$ as formal power series about $r = 0 \in ( - 1 , + 1 )$; convergence is obtained in some neighbourhood of $r = 0$. Observe that the metric $\tilde{g} \in \mathsf{S} ^ { 2 } \mathcal{E}$ trivially satisfies the homogeneity condition 2) over all of $\tilde { N }$. The Riemannian curvature $R (\tilde{ g} )$ is itself conformally invariant by the consequence $R ( \tilde{ g } ) = W ( \tilde { g } ) \in \mathsf{A} ^ { 2 } \tilde{ \mathcal{E} } \otimes \mathsf{A} ^ { 2 } \tilde{ \mathcal{E} }$ of condition 3), and the homogeneity condition implies that any Weyl invariant 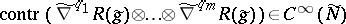restricts over the section $N = N \times \{ 1 \} \times \{ 0 \}$ of $\widetilde { N } = N \times ( 0 , \infty ) \times ( - 1 , + 1 )$ to a Weyl conformal invariant in $C ^ { \infty } ( N )$, as required.

References

[a1]	R. Bach, "Zur Weylschen Relativitätstheorie und der Weylschen Erweiterung des Krümmungstensorbegriffs" Math. Z. , 9 (1921) pp. 110–135 (Also: Jahrbuch 48, 1035) MR1544454 Zbl 48.1035.01
[a2]	T.N. Bailey, M.G. Eastwood, C.R. Graham, "Invariant theory for conformal and CR geometry" Ann. of Math. , 139 : 2 (1994) pp. 491–552 MR1283869 Zbl 0814.53017
[a3]	T.N. Bailey, A.R. Gover, "Exceptional invariants in the parabolic invariant theory of conformal geometry" Proc. Amer. Math. Soc. , 123 (1995) pp. 2535–2543 MR1243161 Zbl 0844.53008
[a4]	S.S. Chern, "An elementary proof of the existence of isothermal parameters on a surface" Proc. Amer. Math. Soc. , 6 (1955) pp. 771–782 MR0074856 Zbl 0066.15402
[a5]	S.S. Chern, "On a conformal invariant of three-dimensional manifolds" , Aspects of Math. and its Appl. , North-Holland (1986) pp. 245–252 MR0849555 Zbl 0589.53011
[a6]	S.S. Chern, J. Simons, "Characteristic forms and geometric invariants" Ann. of Math. , 99 (1974) pp. 48–69 MR0353327 Zbl 0283.53036 Zbl 0591.53050
[a7]	E. Cotton, "Sur les variétes à trois dimensions" Ann. Fac. Sci. Toulouse , 1 (1899) pp. 385–438 (Also: Jahrbuch 30, 538-539) MR1508211 Zbl 30.0538.01
[a8]	C. Fefferman, C.R. Graham, "Conformal invariants" , The Mathematical Heritage of Élie Cartan (Lyon, 1984) , Astérisque (1985) pp. 95–116 MR0837196 Zbl 0602.53007
[a9]	A. Korn, "Zwei Anwendungen der Methode der sukzessiven Anwendungen" Schwarz Festschrift (1914) pp. 215–229 (Also: Jahrbuch 45, 568) Zbl 45.0568.01
[a10]	L. Lichtenstein, "Zur Theorie der konformen Abbildungen nichtanalytischer, singularitätenfreier Flächenstücke auf ebene Gebiete" Bull. Internat. Acad. Sci. Gracovie, Cl. Sci. Math. Nat. Ser. A. (1916) pp. 192–217 (Also: Jahrbuch 46, 547)
[a11]	H. Osborn, "Affine connection complexes" Acta Applic. Math. (to appear) MR1741659 Zbl 0956.53014
[a12]	J.A. Schouten, "Über die konforme Abbildung $n$-dimensionaler Mannigfaltigkeiten mit quadratischer Maß bestimmung auf eine Mannigfaltigkeit mit euklidischer Maß bestimmung" Math. Z. , 11 (1921) pp. 58–88 (Also: Jahrbuch 48, 857-858)
[a13]	J.A. Schouten, J. Haantjes, "Beitgräge zur allgemeinen (gekrümmten) konformen Differentialgeometrie I–II" Math. Ann. , 112/113 (1936) pp. 594–629; 568–583
[a14]	H. Weyl, "Reine Infinitesimalgeometrie" Math. Z. , 2 (1918) pp. 384–411 (Also: Jahrbuch 46, 1301) MR1544327 Zbl 46.1301.01
[a15]	H. Weyl, "The classical groups" , Princeton Univ. Press (1939) (Reprint: 1946) MR0000255 Zbl 0020.20601 Zbl 65.0058.02