Chasles-Cayley-Brill formula

Let $C$ be an irreducible algebraic plane curve of degree $n$, given by an equation $f ( X , Y ) = 0$ where $f$ is an irreducible bivariate polynomial of degree $n$ over a ground field $k$ (cf. also Algebraic curve). For simplicity $k$ is assumed to be algebraically closed (cf. also Algebraically closed field), although most of what is said below can be suitably generalized without that assumption. For the basic field theory involved, see [a6] (or the modernized version [a4]) and [a3]. For much of the geometry to be discussed, see [a5] and [a8]; in particular, for the idea of points at infinity of $C$, see [a1]. For an interplay between the geometry and the algebra, see [a2].

One starts by analyzing when the curve $C$ can be rationally parametrized. For example, the unit circle $X ^ { 2 } + Y ^ { 2 } = 1$ has the rational parametrization

\begin{equation*} X = \frac { 1 - t ^ { 2 } } { 1 + t ^ { 2 } } , Y = \frac { 2 t } { 1 + t ^ { 2 } }. \end{equation*}

Likewise, the cuspidal cubic $Y ^ { 2 } = X ^ { 3 }$ has the rational parametrization $X = t ^ { 2 }$ and $Y = t ^ { 3 }$. However, the non-singular cubic $Y ^ { 2 } = X ^ { 3 } - 1$ does not have any rational parametrization. To obtain the parametrization of the circle, one cuts it by a line of slope $t$ through the point $( - 1,0 )$ and notes that it meets the circle in the variable point

\begin{equation*} \left( \frac { 1 - t ^ { 2 } } { 1 + t ^ { 2 } } , \frac { 2 t } { 1 + t ^ { 2 } } \right). \end{equation*}

For the cuspidal cubic one takes a line through the cusp $( 0,0 )$ and notes that it meets the cubic in the variable point $( t ^ { 2 } , t ^ { 3 } )$. This works because a line meets a circle in $2$ points, and it meets a cubic in $3$ points. In case of a cuspidal cubic two intersections are absorbed in the cusp. In case of a non-singular cubic there is no such point for the absorption. Generalizing this one can show that the curve $C$ cannot have more than $( n - 1 ) ( n - 2 ) / 2$ double points and if it does have that many, then it can be parametrized rationally. To this end one first notes that a bivariate polynomial of degree $m$ has

\begin{equation*} \left( \begin{array} { c } { m + 2 } \\ { 2 } \end{array} \right) = \frac { ( m + 2 ) ( m + 1 ) } { 2 } \end{equation*}

coefficients and hence the dimension of the system $S$ of curves of degree $n - 2$ passing through $( n - 1 ) ( n - 2 ) / 2$ double points of $C$ is $n ( n - 1 ) / 2 - 1 - ( n - 1 ) ( n - 2 ) / 2 = n - 2$. Next, by the Bezout theorem (which is the oldest theorem in algebraic geometry), a curve of degree $n$ and a curve of degree $m$, having no common component, meet in 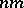points, counted properly. In the proper counting a double point of $C$ should be counted twice. Thus, the number of free points in which $C$ meets a curve $D$ of degree $n - 2$ passing through the $( n - 1 ) ( n - 2 ) / 2$ double points of $C$ is $n ( n - 2 ) - ( n - 1 ) ( n - 2 ) = n - 2$. Since $n - 2$ is also the dimension of the system $S$, the members of $S$ which pass through $n - 3$ fixed simple points of $C$ form a pencil, i.e., a one-parameter family $D _ { t }$, a variable member of which meets $C$ in one variable point whose coordinates are single-valued, and hence rational, functions of $t$. If $C$ had an extra double point, then one can take a value $t_0$ of $t$ so that $D _ { t _ { 0 } }$ goes through it and this would make the properly counted intersections of $C$ and $D _ { t _ { 0 } }$ to be $> n ( n - 2 )$, contradicting the Bezout theorem because $C$ is irreducible and $D _ { t _ { 0 } }$ has smaller degree.

Provisionally defining the genus $g$ of $C$ (cf. also Genus of a curve) by

\begin{equation*} g = \frac { ( n - 1 ) ( n - 2 ) } { 2 } -\#\text{double points}, \end{equation*}

one always has $g \geq 0$, and $g = 0 \Rightarrow C$ is rational, i.e., has a rational parametrization. To make the reverse implication $\Leftarrow $ also true, one must learn to count the double points properly. To begin with, one must include singularities of $C$ at infinity. Next, by looking at the curve $Y ^ { e } = X ^ { d }$, where $e > d$ with $\operatorname { gcd } ( e , d ) = 1$, which is obviously rational and has a $d$-fold point at the origin and an $( e - d )$-fold point at infinity as its only singularities, one decides to count a $d$-fold point as $d ( d - 1 ) / 2$ double points. Before discussing infinitely near singularities, one notes that the degree $n$ of $C$ can be geometrically characterized as the number of points in which a general line meets it.

Likewise, the multiplicity $d$ of a point $P$ of $C$ can be characterized geometrically by saying that $n - d$ is equal to the number of points in which a generic line through $P$ meets $C$ outside $P$; $P$ is a simple or singular point of $C$ according as $d = 1$ or $d > 1$. Algebraically, by translating the coordinates one may assume $P$ to be the origin $( 0,0 )$, and then $d$ is the order of $f$, i.e., $f$ has terms of degree $d$ but none of degree $< d$. By making the quadratic transformation $X = X ^ { \prime }$ and $Y = X ^ { \prime } Y ^ { \prime }$ one gets $f ( X ^ { \prime } , X ^ { \prime } Y ^ { \prime } ) = X ^ { \prime d } f ^ { \prime } ( X ^ { \prime } , Y ^ { \prime } )$, where $C ^ { \prime }$: $f ^ { \prime } ( X ^ { \prime } , Y ^ { \prime } ) = 0$ is the proper transform of $C$. The exceptional line $X ^ { \prime } = 0$ meets $C ^ { \prime }$ in points $P _ { 1 } , \ldots , P _ { h }$ whose multiplicities $d _ { 1 } , \ldots , d _ { h }$ add up to $\leq d$. These are the points of $C$ in the first neighbourhood of $P$. Points in the first neighbourhoods of these points are the points of $C$ in the second neighbourhood of $P$, and so on. It is easily seen that all points in a high enough neighbourhood of $P$ are simple. Now $P$ is counted as $\delta ( P )$ double points, where

\begin{equation*} \delta ( P ) = \sum \frac { d ( Q ) ( d ( Q ) - 1 ) } { 2 } \end{equation*}

with the summation extended over all points $Q$ in the various neighbourhoods of $P$, including $P$; here $d ( Q )$ is the multiplicity of $Q$; clearly: $\delta ( P ) = 0$ $\Leftrightarrow$ $P$ is a simple point of $C$. One arrives at the exact genus formula

\begin{equation*} g = \frac { ( n - 1 ) ( n - 2 ) } { 2 } - \sum \delta ( P ), \end{equation*}

with summation over all points $P$ of $C$. One always has $g \geq 0$; and $g = 0 \Leftrightarrow C$ is rational.

It turns out that $g$ is a birational invariant of $C$, i.e., it remains unchanged when $C$ undergoes a birational transformation (cf. also Birational morphism). The residue class ring of the polynomial ring $k [ X , Y ]$ modulo the ideal generated by $f ( X , Y )$ is the affine coordinate ring of $C$ and is denoted by $k [ C ]$. Note that $k [ C ] = k [ x , y ]$ where $x$, $y$ are the images of $X$, $Y$ in $k [ C ]$. The quotient field $k ( C ) = k ( x , y )$ of $k [ C ]$ is the function field of $C$. A birational correspondence between curves $C$ and $C ^ { * }$ is an almost one-to-one correspondence; it is given by a $k$-isomorphism between $k ( C )$ and $k ( C ^ { * } )$. So one should be able to define $g$ directly in terms of $k ( C )$. Following C.G.J. Jacobi one takes any differential of $k ( C )$ (cf. also Differential field), i.e., an expression of type $ud v$ with $u , v \in k ( C )$, and shows that if the differential is not zero, then the number of its zeros minus the number of its poles equals $2 g - 2$. Having brought the point $P$ of $C$ to the origin, its local ring $R ( P )$ is defined to be the subring of $k ( C )$ consisting of all quotients $r ( x , y ) / s ( x , y )$ where $r ( X , Y )$, $s ( X , Y )$ are polynomials with $s ( 0,0 ) \neq 0$ (cf. also Local ring); its unique maximal ideal $M ( R ( P ) )$ consists of the above quotients with $r ( 0,0 ) = 0$. Let ${\frak C} ( P )$ be the conductor of $R ( P )$, i.e., the largest ideal in $R ( P )$ which remains an ideal in the integral closure $R ^ { \prime } ( P )$ of $R ( P )$ in $k ( C )$. It can be shown that $\delta ( P )$ is the length of ${\frak C} ( P )$ in $R ( P )$, i.e., the maximal length of strictly increasing chains of ideals $\mathfrak { C } ( P ) = I _ { 0 } \subset \ldots \subset I _ { \delta } = R ( P )$ in $R ( P )$; moreover, $2 \delta ( P )$ is the length of ${\frak C} ( P )$ in $R ^ { \prime } ( P )$, which is a ubiquitous result having two dozen proofs in the literature. The ring $R ^ { \prime } ( P )$ has a finite number of maximal ideals and localizing $R ^ { \prime } ( P )$ at them gives discrete valuation rings; as $P$ varies over all points of $C$, including those at infinity, these discrete valuation rings vary over the Riemann surface $\Re ( C )$ of $C$, i.e., the set of all discrete valuation rings whose quotient field is $k ( C )$ and which contain $k$. Let $\mathfrak { R } ( C , P )$ denote the localizations of $R ^ { \prime } ( P )$ at the various maximal ideals in $R ^ { \prime } ( P )$ (cf. also Localization in a commutative algebra); one calls $P$ the centre on $C$ of the members of $\mathfrak { R } ( C , P )$; note that $R ^ { \prime } ( P ) = R ( P )$ $\Leftrightarrow$ $P$ is a simple point of $C$, and hence for all except a finite number of points of $C$, the set $\mathfrak { R } ( C , P )$ has exactly one member. For any $T \in \Re ( C )$ and non-zero $r , s \in k ( C )$ one puts

\begin{equation*} \operatorname { ord } _ { T } ( r / s ) = \lambda - \mu, \end{equation*}

with $r T = M ( T ) ^ { \lambda }$ and $s T = M ( T ) ^ { \mu }$; take $\tau \in T$ with $\tau T = M ( T )$ and define

\begin{equation*} \operatorname { ord } _ { T } ( u d v ) = \operatorname { ord } _ { T } ( u d v / d \tau ); \end{equation*}

one calls $\tau$ a uniformizing parameter of $T$. Now the number of zeros minus number of poles of $ud v$ equals $\sum \text { ord }_{ T } ( u d v )$ taken over all $T$ in $\Re ( C )$. For any point $P$ of $C$, not at infinity, one has Dedekind's formula

\begin{equation*} f _ { Y } ( x , y ) R ^ { \prime } ( P ) = \mathfrak { C } ( P ) \mathfrak { D } ( P , x ), \end{equation*}

where $\mathfrak { D } ( P , x )$ is the different ideal in $R ^ { \prime } ( P )$ defined by saying that $\mathfrak { D } ( P , x ) T = M ( T ) ^ { \epsilon }$ with $\epsilon = \operatorname { ord } _ { T } ( d x / d \tau )$ for every $T \in \Re ( C , P )$.

For $i = 1,2$, let $C_i$ be an irreducible algebraic plane curve such that $k ( C )$ is a finite separable algebraic field extension of $k ( C _ { i } )$ of field degree $\nu _ { i }$ (cf. also Extension of a field; Separable extension). This defines a $( \nu _ { 1 } , \nu _ { 2 } )$ correspondence between $\mathfrak { R } ( C _ { 1 } )$ and $\mathfrak { R } ( C _ { 2 } )$, and hence between $C _ { 1 }$ and $C _ { 2 }$; namely, $T _ { 1 } \in \Re ( C _ { 1 } )$ and $T _ { 2 } \in \Re ( C _ { 2 } )$ correspond if and only if for some $T \in \Re ( C )$ one has $T \cap k ( C _ { 1 } ) = T _ { 1 }$ and $T \cap k ( C _ { 2 } ) = T _ { 2 }$. Let $g_i$ be the genus of $C_i$, let the different $\mathfrak { D } ( C , C _ { i } )$ be the integer-valued function on $\Re ( C )$ whose value at $T$ in $\Re ( C )$ is given by $\operatorname { ord } _ { T } ( d \tau _ { i } / d \tau )$, where $\tau_i$ is a uniformizing parameter of $T \cap k ( C _ { i } )$, and let $\mathfrak { D } _ { i } = \sum \mathfrak { D } ( C , C _ { i } ) ( T )$ with summation over all $T \in \Re ( C )$. Then the Riemann–Hurwitz formula says that

\begin{equation*} 2 g - 2 = \nu _ { i } ( 2 g _ { i } - 2 ) + \mathfrak { D } _ { i }, \end{equation*}

and this gives rise to the Zeuthen formula

\begin{equation*} \nu _ { 1 } ( 2 g _ { 1 } - 2 ) + \mathfrak { D } _ { 1 } = \nu _ { 2 } ( 2 g _ { 2 } - 2 ) + \mathfrak { D } _ { 2 }. \end{equation*}

Now suppose there is a $k$-isomorphism $\phi : k ( C _ { 1 } ) \rightarrow k ( C _ { 2 } )$. Then $T \in \Re ( C )$ is called a fixed place of the correspondence if $T \cap k ( C _ { 2 } ) = \phi ( T \cap k ( C _ { 1 } ) )$. The Chasles–Cayley–Brill formula says that under suitable conditions, the number of these, counted properly, equals $\nu _ { 1 } + \nu _ { 2 } + 2 \gamma g$, where the integer $\gamma$ is called the valence of the correspondence. For details see [a7], pp. 189–194.

In case $k$ is the field of complex numbers, to describe Riemann's approach one topologizes $\Re ( C )$ to make it into a compact orientable two-dimensional real manifold, and hence into a sphere with $g$ handles (cf. also Riemann surface). Likewise, $\mathfrak { R } ( C _ { 1 } )$ is made into a sphere with $g_1$ handles. Triangulate $\mathfrak { R } ( C _ { 1 } )$ by including all the branch points as vertices, and lift this triangulation to a triangulation of $\Re ( C )$. Let $( V _ { 1 } , E _ { 1 } , F _ { 1 } )$ and $( V , E , F )$ be the vertices, edges, faces of the bottom and top triangulations respectively. Then $V = \nu _ { 1 } V _ { 1 } - \mathfrak { D } _ { 1 }$, $E = \nu _ { 1 } E _ { 1 }$, $F = \nu _ { 1 } F _ { 1 }$, and hence by the Euler–Poincaré theorem one obtains

\begin{equation*} 2 g - 2 = \nu _ { 1 } ( 2 g _ { 1 } - 2 ) + \mathfrak { D } _ { 1 }. \end{equation*}

This proves the birational invariance of $g$ and the Riemann–Hurwitz formula. For details, see [a2] and [a4].

References

[a1]	S.S. Abhyankar, "What is the difference between a parabola and a hyperbola" Math. Intelligencer , 10 (1988) pp. 36–43
[a2]	S.S. Abhyankar, "Algebraic geometry for scientists and engineers" , Amer. Math. Soc. (1990) MR1075991 Zbl 0709.14001 Zbl 0721.14001
[a3]	S.S. Abhyankar, "Field extensions" G.A. Pilz (ed.) A.V. Mikhalev (ed.) , Handbook of the Heart of Algebra , Kluwer Acad. Publ. (to appear)
[a4]	C. Chevalley, "Introduction to the theory of algebraic functions of one variable" , Math. Surveys , 6 , Amer. Math. Soc. (1951) MR0042164 Zbl 0045.32301
[a5]	J.L. Coolidge, "A treatise on algebraic plane curves" , Clarendon Press (1931) MR0120551 MR1522528 Zbl 57.0820.06
[a6]	R. Dedekind, H. Weber, "Theorie der algebraischen Functionen einer Veränderlichen" Crelle J. , 92 (1882) pp. 181–290
[a7]	S. Lefschetz, "Algebraic geometry" , Princeton Univ. Press (1953)
[a8]	F. Severi, "Vorlesungen über algebraische Geometrie" , Teubner (1921) MR0245574 Zbl 48.0687.01