Stability theory
A collection of views, presentations, ideas, concepts, arguments, methods, theories (containing definitions, lemmas, theorems, and proofs) arising from and having as its aim the study of the stability of motion (understood in the same wide form). Thus, stability theory is a theory in the widest sense of this word. Among the different concepts of the stability of motion the best known are the following:
1) The concept of stability introduced by A.M. Lyapunov, and its modifications: Lyapunov stability (in particular, asymptotic stability and exponential stability); conditional stability (in particular, asymptotic conditional stability and exponential conditional stability); stability for a part of the variables; uniform stability; stability in the presence of persistently acting perturbations; orbit stability; the presence of attractors (cf. Limit cycle; Lorenz attractor); stochastic stability; absolute stability (cf. Stability, absolute). Cf. also Stability criterion; Stability region.
3) Poisson stability and the concepts related to it (wandering point; complete instability).
4) Structural stability (cf. Rough system) — a concept introduced by A.A. Andronov and L.S. Pontryagin.
5) Preservation of most of the invariant tori of an integrable Hamiltonian system for small perturbations of the Hamiltonian, discovered by A.N. Kolmogorov (cf. Small denominators).
In Lyapunov stability theory (cf. [1], Vol. 2 and also [2]–[4]) one selects questions connected with Lyapunov's first method. Here it is usual to refer to the theory of linear systems of differential equations (cf. Variational equations; Linear system of differential equations with periodic coefficients; Linear system of differential equations with almost-periodic coefficients; Regular linear system of differential equations; Irregularity indices; Almost-reducible linear system of differential equations; Reducible linear system of differential equations; Multipliers; Hamiltonian system, linear) and having a large intersection with the theory of linear systems, the theory of Lyapunov characteristic exponents (cf. Lyapunov characteristic exponent; cf. also Singular exponents; Central exponents; Integral separation condition; Stability of characteristic exponents). For Lyapunov's second method see Lyapunov function, and also [5]–[9].
In the theory of structural stability one singles out the theory of Anosov systems (cf. 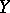 -system, [10]) as well as criteria of structural stability (cf. [11], [12]).
-system, [10]) as well as criteria of structural stability (cf. [11], [12]).
For a study of Lyapunov stability in mechanics one touches upon the following questions: the stability of equilibrium shapes of rotating fluids (cf. [1], Vols. 3–4), of other gravitational systems (cf. [13]), the stability of the motion of fluids (cf. [14], [15]), the stability of motion of deformable rigid bodies (cf. Stability of an elastic system, as well as [16]–[19]), the stability of motion of bodies with cavities containing a fluid [20], the stability of automatic control systems [21], and the stability of the solutions of equations with delay [22].
References
| [1] | A.M. Lyapunov, "Collected works" , 1–5 , Moscow-Leningrad (1954–1965) (In Russian) |
| [2] | R.E. Bellman, "Stability theory of differential equations" , Dover, reprint (1969) |
| [3] | B.P. Demidovich, "Lectures on the mathematical theory of stability" , Moscow (1967) (In Russian) |
| [4] | Yu.L. Daletskii, M.G. Krein, "Stability of solutions of differential equations in Banach space" , Amer. Math. Soc. (1974) (Translated from Russian) |
| [5] | J. La Salle, S. Lefschetz, "Stability by Lyapunov's direct method with applications" , Acad. Press (1961) |
| [6] | V.I. Zubov, "Methods of A.M. Lyapunov and their application" , Noordhoff (1964) (Translated from Russian) |
| [7] | V.V. Rumyantsev, , Mechanics in the USSR during 50 years , 1 , Moscow (1968) (In Russian) |
| [8] | K.G. Valeev, G.S. Finin, "The construction of Lyapunov functions" , Kiev (1981) (In Russian) |
| [9] | A.A. Shestakov, "Theory and application of the general direct Lyapunov method for abstract dynamical systems (a review of the contemporary state of the geometrical approach in the direct Lyapunov method)" Differential Eq. , 18 : 12 (1983) pp. 1458–1485 Diff. Uravn. , 18 : 12 (1982) pp. 2069–2097 |
| [10] | D.V. Anosov, "Geodesic flows on closed Riemann manifolds with negative curvature" Proc. Steklov Inst. Math. , 90 (1967) Trudy Mat. Inst. Steklov. , 90 (1967) |
| [11] | V.A. Pliss, "Integral sets of periodic systems of differential equations" , Moscow (1977) (In Russian) |
| [12] | V.A. Pliss, "Stability of an arbitrary system with respect to perturbations that are small in the sense of 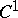 " Diff. Uravn. , 16 : 10 (1980) pp. 1891–1892 (In Russian) " Diff. Uravn. , 16 : 10 (1980) pp. 1891–1892 (In Russian) |
| [13] | V.L. Polyachenko, A.M. Fridman, "Equilibrium and stability of grativational systems" , Moscow (1976) (In Russian) |
| [14] | C.C. Lin, "The theory of hydrodynamic stability" , Cambridge Univ. Press (1955) |
| [15] | D. Joseph, "Stability of fluid motions" , 1–2 , Springer (1976) |
| [16] | V.V. Bolotin, "Nonconservative problems of the theory of elastic stability" , Pergamon (1963) (Translated from Russian) |
| [17] | V.V. Bolotin, E.I. Grigolyuk, , Mechanics in the USSR during 50 years , 3 , Moscow (1972) (In Russian) |
| [18] | A.S. Vol'mir, "Stability of deformable systems" , Moscow (1967) (In Russian) |
| [19] | V.D. Klushnikov, "Stability of elastic-plastic systems" , Moscow (1980) (In Russian) |
| [20] | N.N. Moiseev, V.V. Rumyantsev, "The dynamics of bodies with cavities containing fluids" , Moscow (1965) (In Russian) |
| [21] | J.H. Taylor, "Frequency domain criteria for absolute stability" , Acad. Press (1973) |
| [22] | J.K. Hale, "Functional differential equations" , Springer (1971) |
Comments
Results on the preservation of invariant tori under perturbations of integrable Hamiltonian systems form the subject matter of KAM theory, in particular the Kolmogorov–Arnol'd–Moser theorem, cf. (the editorial comments to) Quasi-periodic motion.
Recently, structural stability has been studied in relation to hyperbolic systems (with no cycle condition). The most far-reaching results, and a survey of earlier work, can be found in [a1].
Vol. 2 of Lyapunov's collected works [1] has been translated as [a2].
References
| [a1] | R. Mañé, "A proof of the  stability conjecture" Publ. Math. IHES , 66 (1988) pp. 161–210 stability conjecture" Publ. Math. IHES , 66 (1988) pp. 161–210 |
| [a2] | A.M. Lyapunov, "Stability of motion" , Acad. Press (1966) (Translated from Russian) |
| [a3] | W. Hahn, "Stability of motion" , Springer (1967) pp. 422 |
Stability theory. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Stability_theory&oldid=11801