Stability in the presence of persistently acting perturbations

A property of the solution 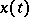, , 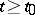of an initial value problem

(*)

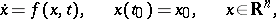which consists of the following. For every 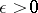there is a 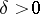such that for every point 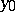satisfying the inequality 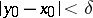, and every mapping 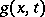satisfying the conditions

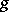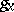a) and are continuous on the set

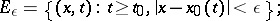b)

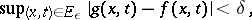the solution 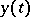of the initial value problem

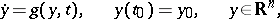is defined for all 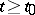and satisfies the inequality

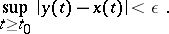Bohl's theorem [1]. Suppose that the initial value problem (*) has a solution 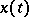, , 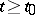satisfying the conditions:

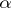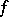) and 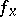are continuous on 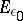for some ;

) ;

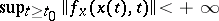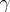) the mapping 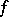is differentiable with respect to at the point 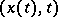for , uniformly with respect to , i.e.

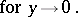Then in order that this solution of the initial value problem be stable in the presence of persistently acting perturbations, it is necessary and sufficient that the upper singular exponent (cf. Singular exponents) of the system of variational equations of the system along the solution 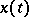be less than zero.

If 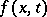does not depend on (an autonomous system) and the solution 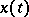is periodic or constant, and also if 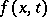is periodic in 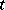and the solution 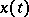is periodic with the same (or a commensurable) period or is a constant, then: 1) the condition stated in Bohl's theorem on uniform differentiability is superfluous (it follows from the remaining conditions of the theorem); and 2) the upper singular exponent of the system of variational equations of the system 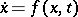along the solution 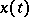can be calculated efficiently.

References

[1]	P. Bohl, "Ueber Differentialgleichungen" J. Reine Angew. Math. (1914) pp. 284–318
[2]	I.G. Malkin, "Theorie der Stabilität einer Bewegung" , R. Oldenbourg , München (1959) (Translated from Russian)
[3]	Yu.L. Daletskii, M.G. Krein, "Stability of solutions of differential equations in Banach space" , Amer. Math. Soc. (1974) (Translated from Russian)

Comments

Stability under persistently acting perturbations is also called stability under persistent perturbations and total stability.

References

[a1]	W. Hahn, "Stability of motion" , Springer (1965) pp. §56 (Translated from German)