Difference between revisions of "Smirnov class"
(Importing text file) |
m (fixing < >) |
||
| (One intermediate revision by one other user not shown) | |||
| Line 1: | Line 1: | ||
| − | + | <!-- | |
| + | s0858301.png | ||
| + | $#A+1 = 28 n = 1 | ||
| + | $#C+1 = 28 : ~/encyclopedia/old_files/data/S085/S.0805830 Smirnov class | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| − | + | {{TEX|auto}} | |
| + | {{TEX|done}} | ||
| − | + | The set $ E _ {p} ( G) $ | |
| + | of all functions $ f( z) $ | ||
| + | holomorphic in a simply-connected domain $ G \subset \mathbf C $ | ||
| + | with rectifiable Jordan boundary $ \Gamma $, | ||
| + | such that for every function in it there is a sequence of closed rectifiable Jordan curves $ \Gamma _ {n} ( f ) \subset G $, | ||
| + | $ n = 1, 2 \dots $ | ||
| + | with the following properties: | ||
| + | |||
| + | 1) $ \Gamma _ {n} ( f ) $ | ||
| + | tends to $ \Gamma $ | ||
| + | as $ n \rightarrow \infty $ | ||
| + | in the sense that if $ G _ {n} ( f ) $ | ||
| + | is the bounded domain with boundary $ \Gamma _ {n} ( f ) $, | ||
| + | then | ||
| + | |||
| + | $$ | ||
| + | G _ {1} ( f ) \subset \dots \subset G _ {n} ( f ) \subset G \ \ | ||
| + | \textrm{ and } \ \cup _ {n= 1 } ^ \infty G _ {n} ( f ) = G; | ||
| + | $$ | ||
2) | 2) | ||
| − | < | + | $$ |
| + | \sup _ { n } \left \{ \int\limits _ {\Gamma _ {n} ( f ) } | ||
| + | | f( z) | ^ {p} | dz | \right \} < \infty \ ( p> 0 \ | ||
| + | \textrm{ fixed } ). | ||
| + | $$ | ||
| − | This definition was proposed by M.V. Keldysh and M.A. Lavrent'ev [[#References|[2]]], and is equivalent to V.I. Smirnov's definition [[#References|[1]]] in which curves | + | This definition was proposed by M.V. Keldysh and M.A. Lavrent'ev [[#References|[2]]], and is equivalent to V.I. Smirnov's definition [[#References|[1]]] in which curves $ \gamma ( \rho ) $ |
| + | are used instead of $ \Gamma _ {n} ( f ) $. | ||
| + | These curves are the images of the circles $ | w | = \rho < 1 $ | ||
| + | under some univalent [[Conformal mapping|conformal mapping]] $ z= \phi ( w) $ | ||
| + | from the disc $ | w | < 1 $ | ||
| + | onto the domain $ G $, | ||
| + | and the supremum is taken over all $ \rho \in ( 0, 1) $. | ||
| − | The classes | + | The classes $ E _ {p} ( G) $ |
| + | are the best known and most thoroughly studied generalization of the [[Hardy classes|Hardy classes]] $ H _ {p} $, | ||
| + | and are connected with them by the following relation: $ f \in E _ {p} ( G) $ | ||
| + | if and only if | ||
| − | + | $$ | |
| + | f( \phi ( w))( \phi ^ \prime ( w)) ^ {1/p} \in H _ {p} . | ||
| + | $$ | ||
| − | The properties of the classes | + | The properties of the classes $ E _ {p} ( G) $ |
| + | are closest to those of $ H _ {p} $ | ||
| + | in the case when $ G $ | ||
| + | is a [[Smirnov domain|Smirnov domain]]. They have been generalized to domains $ G $ | ||
| + | with boundaries of finite Hausdorff length. See also [[Boundary properties of analytic functions|Boundary properties of analytic functions]]. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> V.I. Smirnov, "Sur les formules de Cauchy et de Green et quelques problèmes qui s'y rattachent" ''Izv. Akad. Nauk SSSR. Otdel. Mat. i Estestv. Nauk'' , '''3''' (1932) pp. 337–372</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> M.V. Keldysh, M.A. Lavrent'ev, "Sur la répresentation conforme des domaines limités par des courbes rectifiables" ''Ann. Sci. Ecole Norm. Sup.'' , '''54''' (1937) pp. 1–38</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> I.I. [I.I. Privalov] Priwalow, "Randeigenschaften analytischer Funktionen" , Deutsch. Verlag Wissenschaft. (1956) (Translated from Russian)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> G.M. Goluzin, "Geometric theory of functions of a complex variable" , ''Transl. Math. Monogr.'' , '''26''' , Amer. Math. Soc. (1969) (Translated from Russian)</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> P.L. Duren, "Theory of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085830/s08583029.png" /> spaces" , Acad. Press (1970)</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> V.I. Smirnov, "Sur les formules de Cauchy et de Green et quelques problèmes qui s'y rattachent" ''Izv. Akad. Nauk SSSR. Otdel. Mat. i Estestv. Nauk'' , '''3''' (1932) pp. 337–372</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> M.V. Keldysh, M.A. Lavrent'ev, "Sur la répresentation conforme des domaines limités par des courbes rectifiables" ''Ann. Sci. Ecole Norm. Sup.'' , '''54''' (1937) pp. 1–38</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> I.I. [I.I. Privalov] Priwalow, "Randeigenschaften analytischer Funktionen" , Deutsch. Verlag Wissenschaft. (1956) (Translated from Russian)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> G.M. Goluzin, "Geometric theory of functions of a complex variable" , ''Transl. Math. Monogr.'' , '''26''' , Amer. Math. Soc. (1969) (Translated from Russian)</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> P.L. Duren, "Theory of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085830/s08583029.png" /> spaces" , Acad. Press (1970)</TD></TR></table> | ||
Latest revision as of 01:28, 26 April 2022
The set $ E _ {p} ( G) $
of all functions $ f( z) $
holomorphic in a simply-connected domain $ G \subset \mathbf C $
with rectifiable Jordan boundary $ \Gamma $,
such that for every function in it there is a sequence of closed rectifiable Jordan curves $ \Gamma _ {n} ( f ) \subset G $,
$ n = 1, 2 \dots $
with the following properties:
1) $ \Gamma _ {n} ( f ) $ tends to $ \Gamma $ as $ n \rightarrow \infty $ in the sense that if $ G _ {n} ( f ) $ is the bounded domain with boundary $ \Gamma _ {n} ( f ) $, then
$$ G _ {1} ( f ) \subset \dots \subset G _ {n} ( f ) \subset G \ \ \textrm{ and } \ \cup _ {n= 1 } ^ \infty G _ {n} ( f ) = G; $$
2)
$$ \sup _ { n } \left \{ \int\limits _ {\Gamma _ {n} ( f ) } | f( z) | ^ {p} | dz | \right \} < \infty \ ( p> 0 \ \textrm{ fixed } ). $$
This definition was proposed by M.V. Keldysh and M.A. Lavrent'ev [2], and is equivalent to V.I. Smirnov's definition [1] in which curves $ \gamma ( \rho ) $ are used instead of $ \Gamma _ {n} ( f ) $. These curves are the images of the circles $ | w | = \rho < 1 $ under some univalent conformal mapping $ z= \phi ( w) $ from the disc $ | w | < 1 $ onto the domain $ G $, and the supremum is taken over all $ \rho \in ( 0, 1) $.
The classes $ E _ {p} ( G) $ are the best known and most thoroughly studied generalization of the Hardy classes $ H _ {p} $, and are connected with them by the following relation: $ f \in E _ {p} ( G) $ if and only if
$$ f( \phi ( w))( \phi ^ \prime ( w)) ^ {1/p} \in H _ {p} . $$
The properties of the classes $ E _ {p} ( G) $ are closest to those of $ H _ {p} $ in the case when $ G $ is a Smirnov domain. They have been generalized to domains $ G $ with boundaries of finite Hausdorff length. See also Boundary properties of analytic functions.
References
| [1] | V.I. Smirnov, "Sur les formules de Cauchy et de Green et quelques problèmes qui s'y rattachent" Izv. Akad. Nauk SSSR. Otdel. Mat. i Estestv. Nauk , 3 (1932) pp. 337–372 |
| [2] | M.V. Keldysh, M.A. Lavrent'ev, "Sur la répresentation conforme des domaines limités par des courbes rectifiables" Ann. Sci. Ecole Norm. Sup. , 54 (1937) pp. 1–38 |
| [3] | I.I. [I.I. Privalov] Priwalow, "Randeigenschaften analytischer Funktionen" , Deutsch. Verlag Wissenschaft. (1956) (Translated from Russian) |
| [4] | G.M. Goluzin, "Geometric theory of functions of a complex variable" , Transl. Math. Monogr. , 26 , Amer. Math. Soc. (1969) (Translated from Russian) |
| [5] | P.L. Duren, "Theory of 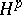 spaces" , Acad. Press (1970) spaces" , Acad. Press (1970) |
Smirnov class. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Smirnov_class&oldid=14423