Rank

A concept closely connected with the concept of a basis. Usually rank is defined either as the minimal cardinality of a generating set (in this way, for example, one introduces the basis rank of an algebraic system), or as the maximal cardinality of a subsystem of elements which are independent in a certain sense.

The rank of a system of a vectors in a vector space over a skew-field is the maximal number of linearly independent vectors in this system (see Linear independence). The rank, or dimension, of a vector space, in particular, is equal to the number of elements in a basis of this space (the rank does not depend on the choice of the basis: all bases have the same cardinality). For a module the situation is more complicated. There exist associative rings 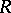such that even a free module over 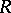can have two bases with a different number of elements (see Rank of a module; Free module). If each free 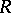-module has a unique rank, then 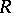is said to have the invariant basis number property. Every commutative associative ring with a unit is such, so one can define, for example, the (Prüfer) rank of an Abelian group (which can be considered as a module over the ring 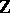). In the non-Abelian case two concepts of the rank of a group are introduced, the general and the special rank (see Rank of a group). One defines the rank of an algebraic group and the rank of a Lie group in a special way.

The rank of an algebra (over a skew-field) is understood to be the rank of its additive vector space. However, there exists another, unrelated, concept of rank in the theory of Lie algebras (see Rank of a Lie algebra).

The rank of a matrix is defined as the rank of the system of vectors forming its rows (row rank) or of the system of columns (column rank). For matrices over a commutative ring with a unit these two concepts of rank coincide. For a matrix over a field the rank is also equal to the maximal order of a non-zero minor. The rank of a product of matrices is not greater than the rank of each of the factors. The rank of a matrix does not change under multiplication by a non-singular matrix.

The rank of a linear mapping is the dimension of the image under this mapping. In the finite-dimensional case it coincides with the rank of a matrix of this mapping.

One also introduces the concept of the rank of a bilinear form (see Bilinear form) and the rank of a quadratic form (see Quadratic form). They also (in the finite-dimensional case) coincide with the rank of a matrix of the corresponding form.

Comments

The invariant basis number property is also called the invariant dimension property.

For matrices over skew-fields one considers two ranks, which need not be equal: 1) the rank of the rows considered in a left vector space (it equals the rank of the columns considered in a right vector space); and 2) the rank obtained by interchanging "left" and "right" in 1).

References

[a1]	P.M. Cohn, "Algebra" , 1–3 , Wiley (1988)
[a2]	N. Bourbaki, "Elements of mathematics. Algebra I" , Addison-Wesley (1974) pp. Chapt. II (Translated from French)