P-divisible group
Barsotti–Tate group
A generalization of the concept of a commutative formal group of finite height. The homomorphism induced by multiplication by the prime number $ p $ is an epimorphism for a $ p $- divisible group.
Let $ S $ be a scheme and let $ p $ be a prime number. A $ p $- divisible group of height $ h $ is an inductive system $ G = ( G _ {n} , i _ {n} ) $ of commutative finite group schemes $ G _ {n} $ of order $ p ^ {nh} $( cf. Group scheme) such that the sequences
$$ 0 \rightarrow G _ {n} \rightarrow ^ { {i _ n} } G _ {n+} 1 \rightarrow ^ { {\phi _ n} } \ G _ {n+} 1 $$
are exact (cf. Exact sequence; here $ \phi _ {n} $ is the homomorphism of multiplication by $ p ^ {n} $). A morphism of $ p $- divisible groups is a morphism of the inductive systems. A $ p $- divisible group is said to be connected (respectively, étale) if all $ G _ {n} $ are connected (respectively, étale) group schemes. A connected $ p $- divisible group over a field of characteristic $ p $ is a commutative formal group (considered as the inductive limit of the kernels of $ \phi _ {n} $, i.e. of multiplication by $ p ^ {n} $) for which multiplication by $ p $ is an isogeny [6]. This fact is generalized to include the case of an arbitrary base scheme $ S $ on which the homomorphism induced by multiplication by $ p $ is locally nilpotent [4]. The category of étale $ p $- divisible groups is equivalent to the category of $ p $- adic representations of the fundamental group of the scheme $ S $. Each $ p $- divisible group $ G $ over an Artinian scheme $ S $ contains a maximal connected subgroup $ G ^ {0} $, which is known as the connected component of the identity, the quotient by which is an étale $ p $- divisible group. The dimension of the Lie algebra of any $ {( G ^ {0} ) } _ {n} $ is said to be the dimension of the $ p $- divisible group $ G $.
Let $ A $ be an Abelian variety over the field $ k $ of dimension $ d $, let $ A ( n) $ be the kernel of the homomorphism of multiplication by $ p ^ {n} $ in $ A $ and let $ i _ {n} : A ( n) \rightarrow A ( n + 1 ) $ be a natural inclusion. The inductive system $ A ( \infty ) = ( A ( n) , i _ {n} ) $ is a $ p $- divisible group of height $ 2d $. Its connected component of the identity $ A ( \infty ) ^ {0} $ coincides with the formal completion of $ A $ along the unit section, while the height of $ A ( \infty ) ^ {0} $ equals $ 2 \mathop{\rm dim} A $.
Let $ G = ( G _ {n} , i _ {n} ) $ be a $ p $- divisible group of height $ h $, let $ {\widehat{G} } _ {n} $ denote the Cartier dual finite group schemes and let $ \widehat{i} _ {n} : \widehat{G} _ {n} \rightarrow \widehat{G} _ {n+} 1 $ be the mapping dual to the mapping of multiplication by $ p : G _ {n+} 1 \rightarrow G _ {n} $. The system $ \widehat{G} = ( \widehat{G} _ {n} , \widehat{i} _ {n} ) $ is then a $ p $- divisible group of height $ h $ and is called the Serre dual to the $ p $- divisible group $ G $. The sum of the dimensions of $ G $ and $ \widehat{G} $ is equal to $ h $.
As in formal groups, so, too, in $ p $- divisible groups, the concept of a Dieudonné module, which plays an important role in the deformation theory of $ p $- divisible groups [2], [3], [4] may be introduced.
If $ S $ is the spectrum of an unequal-characteristic discrete valuation ring $ A $ with residue field of characteristic $ p $, the structure of a $ p $- divisible group is closely connected with the structure of the completion of the algebraic closure of the quotient field $ K $ of $ A $, considered as a module over the Galois group of the field $ K $[6].
References
| [1] | I. Barsotti, "Analytic methods for abelian varieties in positive characteristic" , Coll. Théorie des Groupes Algébriques (Bruxelles, 1962) , Gauthier-Villars (1962) pp. 77–85 |
| [2] | A. Grothendieck, "Groupes de Barsotti–Tate et cristaux" , Proc. Internat. Congress Mathematicians (Nice, 1970) , 1 , Gauthier-Villars (1971) pp. 431–436 |
| [3] | B. Mazur, W. Messing, "Universal extensions and one-dimensional crystalline cohomology" , Springer (1974) |
| [4] | W. Messing, "The crystals associated to Barsotti–Tate groups: with applications to Abelian schemes" , Springer (1972) |
| [5] | J.-P. Serre, "Groupes 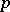 -divisibles (d'après J. Tate)" , Sem. Bourbaki , 318 , Benjamin (1968) -divisibles (d'après J. Tate)" , Sem. Bourbaki , 318 , Benjamin (1968) |
| [6] | J.T. Tate, "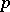 -divisible groups" T.A. Springer (ed.) et al. (ed.) , Proc. Conf. local fields (Driebergen, 1966) , Springer (1967) pp. 158–183 -divisible groups" T.A. Springer (ed.) et al. (ed.) , Proc. Conf. local fields (Driebergen, 1966) , Springer (1967) pp. 158–183 |
Comments
References
| [a1] | M. Demazure, "Lectures on 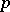 -divisible groups" , Lect. notes in math. , 302 , Springer (1972) -divisible groups" , Lect. notes in math. , 302 , Springer (1972) |
P-divisible group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=P-divisible_group&oldid=48092