Difference between revisions of "Mordell conjecture"
(Category:Algebraic geometry, Category:Number theory) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| − | + | <!-- | |
| + | m0649101.png | ||
| + | $#A+1 = 31 n = 1 | ||
| + | $#C+1 = 31 : ~/encyclopedia/old_files/data/M064/M.0604910 Mordell conjecture | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| − | + | {{TEX|auto}} | |
| + | {{TEX|done}} | ||
| − | of the rational points | + | A conjecture on the finiteness of the set of rational points on an [[Algebraic curve|algebraic curve]] of genus $ g > 1 $. |
| + | Advanced by L.J. Mordell [[#References|[1]]] for the case when the ground field $ K $ | ||
| + | is the field of rational numbers. At present (1982) Mordell's conjecture is taken to be the assertion of the finiteness of the set of rational points $ X ( L) $ | ||
| + | of an irreducible algebraic curve $ X $ | ||
| + | of genus $ g > 1 $ | ||
| + | defined over a field $ K $ | ||
| + | of finite type over the field of rational numbers $ \mathbf Q $ | ||
| + | in any finite extension $ L / K $. | ||
| + | A reduction of Mordell's conjecture to the most difficult case when $ K $ | ||
| + | is an algebraic number field has been obtained (see [[#References|[3]]]). A number of special results related to Mordell's conjecture are known. Thus, it has been proved [[#References|[2]]] that $ X ( K) $ | ||
| + | is finite if the rank of the group of $ K $- | ||
| + | automorphisms from $ X $ | ||
| + | into an elliptic curve $ Y $ | ||
| + | is larger than the rank of the group $ Y ( K) $. | ||
| + | The finiteness of $ X ( K) $ | ||
| + | has been established, [[#References|[7]]], for the broad class of modular curves (cf. [[Modular curve|Modular curve]]) and their fields of definition $ K $. | ||
| + | An estimate for the growth of the height, | ||
| + | |||
| + | $$ | ||
| + | h ( x _ {n} ) \geq \mathop{\rm exp} ( a n + b ) , | ||
| + | $$ | ||
| + | |||
| + | of the rational points $ x _ {n} \in X ( K) $ | ||
| + | has been found, [[#References|[8]]], showing that they are situated more "sparsely" than on the curves of genus $ g \leq 1 $. | ||
| + | It has also been proved that Mordell's conjecture is a consequence of Shafarevich's conjecture on the finiteness of the number of algebraic curves having a given genus $ g > 1 $, | ||
| + | a given field of definition (a finite extension of $ \mathbf Q $) | ||
| + | and a given set of points of bad reduction (see [[#References|[4]]], and also [[Siegel theorem|Siegel theorem]] on integer points). | ||
The geometric analogue of Mordell's conjecture is the assertion of the finiteness of the number of sections of a bundle | The geometric analogue of Mordell's conjecture is the assertion of the finiteness of the number of sections of a bundle | ||
| − | + | $$ | |
| + | f : V \rightarrow B , | ||
| + | $$ | ||
| − | where | + | where $ V $ |
| + | is a non-singular projective surface, $ B $ | ||
| + | is a curve and the general fibre of $ f $ | ||
| + | is an irreducible curve of genus $ g > 1 $. | ||
| + | This assertion is true if the bundle is non-constant, that is, if it is not a direct product after a certain covering of the base $ B $, | ||
| + | and if the characteristic of the ground field $ k $ | ||
| + | is equal to zero (see [[#References|[3]]], [[#References|[6]]]). For constant bundles it is possible only to assert the finiteness of the number of classes consisting of sections that are algebraically equivalent as curves on $ V $. | ||
| + | If the characteristic of $ k $ | ||
| + | is positive, the geometric analogue of Mordell's conjecture is false [[#References|[4]]]. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> L.J. Mordell, "On the rational solutions of the indeterminate equation of the third and fourth degrees" ''Proc. Cambridge Philos. Soc.'' , '''21''' (1922) pp. 179–192</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> V.A. Dem'yanenko, "Rational points of a class of algebraic curves" ''Izv. Akad. Nauk SSSR Ser. Mat.'' , '''30''' : 6 (1966) pp. 1373–1396 (In Russian) {{MR|}} {{ZBL|0162.24502}} </TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> Yu.I. Manin, "Rational points of algebraic curves over function fields" ''Transl. Amer. Math. Soc. (2)'' , '''50''' (1966) pp. 189–234 ''Izv. Akad. Nauk SSSR Ser. Mat.'' , '''27''' : 6 (1963) pp. 1395–1440 {{MR|}} {{ZBL|0178.55102}} </TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> A.N. Parshin, "Quelques conjectures de finitude en géométrie diophantienne" , ''Proc. Internat. Congress Mathematicians (Nice, 1970)'' , '''1''' , Gauthier-Villars (1971) pp. 467–471</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> H. Grauert, "Modell's Vermutung über rationale Punkte auf algebraischen Kurven und Funktionenkörpern" ''Publ. Math. IHES'' : 25 (1965) pp. 131–149</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> S. Lang, "Diophantine geometry" , Interscience (1962) {{MR|0142550}} {{ZBL|0115.38701}} </TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> B. Mazur, "Rational points on modular curves" J.-P. Serre (ed.) P. Deligne (ed.) W. Kuyk (ed.) , ''Modular functions of one variable. 5'' , ''Lect. notes in math.'' , '''601''' , Springer (1977) pp. 107–148 {{MR|0450283}} {{ZBL|0357.14005}} </TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> D. Mumford, "A remark on Mordell's conjecture" ''Amer. J. Math.'' , '''87''' : 4 (1965) pp. 1007–1016 {{MR|186624}} {{ZBL|}} </TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> L.J. Mordell, "On the rational solutions of the indeterminate equation of the third and fourth degrees" ''Proc. Cambridge Philos. Soc.'' , '''21''' (1922) pp. 179–192</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> V.A. Dem'yanenko, "Rational points of a class of algebraic curves" ''Izv. Akad. Nauk SSSR Ser. Mat.'' , '''30''' : 6 (1966) pp. 1373–1396 (In Russian) {{MR|}} {{ZBL|0162.24502}} </TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> Yu.I. Manin, "Rational points of algebraic curves over function fields" ''Transl. Amer. Math. Soc. (2)'' , '''50''' (1966) pp. 189–234 ''Izv. Akad. Nauk SSSR Ser. Mat.'' , '''27''' : 6 (1963) pp. 1395–1440 {{MR|}} {{ZBL|0178.55102}} </TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> A.N. Parshin, "Quelques conjectures de finitude en géométrie diophantienne" , ''Proc. Internat. Congress Mathematicians (Nice, 1970)'' , '''1''' , Gauthier-Villars (1971) pp. 467–471</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> H. Grauert, "Modell's Vermutung über rationale Punkte auf algebraischen Kurven und Funktionenkörpern" ''Publ. Math. IHES'' : 25 (1965) pp. 131–149</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> S. Lang, "Diophantine geometry" , Interscience (1962) {{MR|0142550}} {{ZBL|0115.38701}} </TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> B. Mazur, "Rational points on modular curves" J.-P. Serre (ed.) P. Deligne (ed.) W. Kuyk (ed.) , ''Modular functions of one variable. 5'' , ''Lect. notes in math.'' , '''601''' , Springer (1977) pp. 107–148 {{MR|0450283}} {{ZBL|0357.14005}} </TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> D. Mumford, "A remark on Mordell's conjecture" ''Amer. J. Math.'' , '''87''' : 4 (1965) pp. 1007–1016 {{MR|186624}} {{ZBL|}} </TD></TR></table> | ||
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
The article above was originally written in 1982. Since then much has happened, and the field of arithmetic algebraic geometry has taken on additional prominence. | The article above was originally written in 1982. Since then much has happened, and the field of arithmetic algebraic geometry has taken on additional prominence. | ||
| − | The Mordell conjecture over a number field has been proved in 1983 by G. Faltings. In his fundamental paper [[#References|[a1]]], opening a new chapter in arithmetic algebraic geometry, Faltings proves at the same time two other famous conjectures, namely the Tate conjecture concerning endomorphisms of Abelian varieties over number fields (cf. [[Tate conjectures|Tate conjectures]]) and the Shafarevich conjecture concerning the finiteness of isomorphism classes of curves of genus | + | The Mordell conjecture over a number field has been proved in 1983 by G. Faltings. In his fundamental paper [[#References|[a1]]], opening a new chapter in arithmetic algebraic geometry, Faltings proves at the same time two other famous conjectures, namely the Tate conjecture concerning endomorphisms of Abelian varieties over number fields (cf. [[Tate conjectures|Tate conjectures]]) and the Shafarevich conjecture concerning the finiteness of isomorphism classes of curves of genus $ g $( |
| + | respectively, Abelian varieties) defined over a number field and with good reduction outside a finite number of given places. The relation of the Mordell conjecture with the Shafarevich conjecture was pointed out by A.N. Parshin in 1970 [[#References|[4]]]. Important for the work of Faltings were ideas of S.Yu. Arakelov, Yu.G. Zarkhin and L. Szpiro; essential in Faltings' proof is the theory of heights on the moduli space of Abelian varieties. For a good introduction to the proof of the Mordell conjecture see [[#References|[a5]]]. | ||
====References==== | ====References==== | ||
Latest revision as of 08:01, 6 June 2020
A conjecture on the finiteness of the set of rational points on an algebraic curve of genus $ g > 1 $.
Advanced by L.J. Mordell [1] for the case when the ground field $ K $
is the field of rational numbers. At present (1982) Mordell's conjecture is taken to be the assertion of the finiteness of the set of rational points $ X ( L) $
of an irreducible algebraic curve $ X $
of genus $ g > 1 $
defined over a field $ K $
of finite type over the field of rational numbers $ \mathbf Q $
in any finite extension $ L / K $.
A reduction of Mordell's conjecture to the most difficult case when $ K $
is an algebraic number field has been obtained (see [3]). A number of special results related to Mordell's conjecture are known. Thus, it has been proved [2] that $ X ( K) $
is finite if the rank of the group of $ K $-
automorphisms from $ X $
into an elliptic curve $ Y $
is larger than the rank of the group $ Y ( K) $.
The finiteness of $ X ( K) $
has been established, [7], for the broad class of modular curves (cf. Modular curve) and their fields of definition $ K $.
An estimate for the growth of the height,
$$ h ( x _ {n} ) \geq \mathop{\rm exp} ( a n + b ) , $$
of the rational points $ x _ {n} \in X ( K) $ has been found, [8], showing that they are situated more "sparsely" than on the curves of genus $ g \leq 1 $. It has also been proved that Mordell's conjecture is a consequence of Shafarevich's conjecture on the finiteness of the number of algebraic curves having a given genus $ g > 1 $, a given field of definition (a finite extension of $ \mathbf Q $) and a given set of points of bad reduction (see [4], and also Siegel theorem on integer points).
The geometric analogue of Mordell's conjecture is the assertion of the finiteness of the number of sections of a bundle
$$ f : V \rightarrow B , $$
where $ V $ is a non-singular projective surface, $ B $ is a curve and the general fibre of $ f $ is an irreducible curve of genus $ g > 1 $. This assertion is true if the bundle is non-constant, that is, if it is not a direct product after a certain covering of the base $ B $, and if the characteristic of the ground field $ k $ is equal to zero (see [3], [6]). For constant bundles it is possible only to assert the finiteness of the number of classes consisting of sections that are algebraically equivalent as curves on $ V $. If the characteristic of $ k $ is positive, the geometric analogue of Mordell's conjecture is false [4].
References
| [1] | L.J. Mordell, "On the rational solutions of the indeterminate equation of the third and fourth degrees" Proc. Cambridge Philos. Soc. , 21 (1922) pp. 179–192 |
| [2] | V.A. Dem'yanenko, "Rational points of a class of algebraic curves" Izv. Akad. Nauk SSSR Ser. Mat. , 30 : 6 (1966) pp. 1373–1396 (In Russian) Zbl 0162.24502 |
| [3] | Yu.I. Manin, "Rational points of algebraic curves over function fields" Transl. Amer. Math. Soc. (2) , 50 (1966) pp. 189–234 Izv. Akad. Nauk SSSR Ser. Mat. , 27 : 6 (1963) pp. 1395–1440 Zbl 0178.55102 |
| [4] | A.N. Parshin, "Quelques conjectures de finitude en géométrie diophantienne" , Proc. Internat. Congress Mathematicians (Nice, 1970) , 1 , Gauthier-Villars (1971) pp. 467–471 |
| [5] | H. Grauert, "Modell's Vermutung über rationale Punkte auf algebraischen Kurven und Funktionenkörpern" Publ. Math. IHES : 25 (1965) pp. 131–149 |
| [6] | S. Lang, "Diophantine geometry" , Interscience (1962) MR0142550 Zbl 0115.38701 |
| [7] | B. Mazur, "Rational points on modular curves" J.-P. Serre (ed.) P. Deligne (ed.) W. Kuyk (ed.) , Modular functions of one variable. 5 , Lect. notes in math. , 601 , Springer (1977) pp. 107–148 MR0450283 Zbl 0357.14005 |
| [8] | D. Mumford, "A remark on Mordell's conjecture" Amer. J. Math. , 87 : 4 (1965) pp. 1007–1016 MR186624 |
Comments
The article above was originally written in 1982. Since then much has happened, and the field of arithmetic algebraic geometry has taken on additional prominence.
The Mordell conjecture over a number field has been proved in 1983 by G. Faltings. In his fundamental paper [a1], opening a new chapter in arithmetic algebraic geometry, Faltings proves at the same time two other famous conjectures, namely the Tate conjecture concerning endomorphisms of Abelian varieties over number fields (cf. Tate conjectures) and the Shafarevich conjecture concerning the finiteness of isomorphism classes of curves of genus $ g $( respectively, Abelian varieties) defined over a number field and with good reduction outside a finite number of given places. The relation of the Mordell conjecture with the Shafarevich conjecture was pointed out by A.N. Parshin in 1970 [4]. Important for the work of Faltings were ideas of S.Yu. Arakelov, Yu.G. Zarkhin and L. Szpiro; essential in Faltings' proof is the theory of heights on the moduli space of Abelian varieties. For a good introduction to the proof of the Mordell conjecture see [a5].
References
| [a1] | G. Faltings, "Endlichkeitssätze für abelsche Varietäten über Zahlkörper" Invent. Math. , 73 (1983) pp. 349–366 (Erratum: Ibid 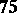 (1984), 381) (1984), 381) |
| [a2] | G. Faltings, "Die Vermutungen von Tate und Mordell" Jhber. Deutsch. Math. Verein. , 86 (1984) pp. 1–13 MR0736624 Zbl 0586.14012 |
| [a3] | P. Deligne, "Preuve et conjectures de Tate et de Shafarevich" Sém. Bourbaki , 616 (1983) Zbl 0591.14026 |
| [a4] | L. Szpiro, "Le conjecture de Mordell" Sém. Bourbaki , 619 (1983) |
| [a5] | G. Faltings (ed.) G. Wüstholtz (ed.) , Rational points , Vieweg (1984) MR0766568 Zbl 0588.14027 |
Mordell conjecture. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Mordell_conjecture&oldid=47899