Gershgorin theorem
Gerschgorin theorem, Geršgorin theorem
Given a complex $( n \times n )$-matrix, $A = [ a_{i, j} ]$, with $n \geq 2$, then finding the eigenvalues of $A$ is equivalent to finding the $n$ zeros of its associated characteristic polynomial
\begin{equation*} p _ { n } ( z ) : = \operatorname { det } \{ z I - A \}, \end{equation*}
where $I$ is the identity $( n \times n )$-matrix (cf. also Matrix; Eigen value). But for $n$ large, finding these zeros can be a daunting problem. Is there an "easy" procedure which estimates these eigenvalues, without having to explicitly form the characteristic polynomial $p _ { n } ( z )$ above and then to find its zeros? This was first considered in 1931 by the Russian mathematician S. Gershgorin, who established the following result [a1]. If $\Delta _ { \delta } ( \alpha ) : = \{ z \in \mathbf{C} : | z - \alpha | \leq \delta \}$ denotes the closed complex disc having centre $\alpha$ and radius $\delta$, then Gershgorin showed that for each eigenvalue $\lambda$ of the given complex $( n \times n )$-matrix $A = [ a_{i, j} ]$ there is a positive integer $i$, with $1 \leq i \leq n$, such that $\lambda \in G _ { i } ( A )$, where
\begin{equation} \tag{a1} G _ { i } ( A ) : = \Delta _ { r _ { i } ( A )} ( a _ { i , i } ) \end{equation}
with
\begin{equation*} r _ { i } ( A ) : = \sum _ { j = 1 \atop j \neq i } ^ { n } | a _ { i , j } |. \end{equation*}
($G _ { r_ i } ( A )$ is called the $i$th Gershgorin disc for $A$.) As this is true for each eigenvalue $\lambda$ of $A$, it is evident that if $\sigma ( A )$ denotes the set of all eigenvalues of $A$, then
\begin{equation} \tag{a2} \sigma ( A ) \subseteq \cup _ { i = 1 } ^ { n } G _ { i } ( A ). \end{equation}
Indeed, let $\lambda$ be any eigenvalue of $A = [ a_{i, j} ]$, so that there is a complex vector $\mathbf x = [ x _ { 1 } \ldots x _ { n } ] ^ { T }$, with $ \mathbf{x} \neq \mathbf{O}$, such that $A \mathbf{x} = \lambda \mathbf{x}$. As $ \mathbf{x} \neq \mathbf{O}$, then $\operatorname { max } _ { 1 \leq j \leq n } | x _ { j } | > 0$, and there is an $i$, with $1 \leq i \leq n$, such that $| x _ { i } | = \operatorname { max } _ { 1 \leq j \leq n } | x _ { j } |$. Taking the $i$th component of $A \mathbf{x} = \lambda \mathbf{x}$ gives $\sum _ { j = 1 } ^ { n } a _ { i ,\, j }\, x _ { j } = \lambda x _ { i }$, or equivalently
\begin{equation*} ( \lambda - a _ { i , i} ) x _ { i } = \sum _ { j = 1 \atop j \neq i } ^ { n } a _ { i ,\, j } x _ { j }. \end{equation*}
On taking absolute values in the above expression and using the triangle inequality, this gives
\begin{equation} \tag{a3} | \lambda - a _ { i , i} | . | x _ { i } | \leq \sum _ { \substack{j = 1 \\ j \neq i }} ^ { n } | a _ { i , j} | . | x _ { j } | \leq r _ { i } ( A ) . | x _ { i } |, \end{equation}
the last inequality following from the definition of $r _ { i } ( A )$ in (a1) and the fact that $| x _ { j } | \leq | x _ { i }|$ for all $1 \leq j \leq n$. Dividing through by $| x _ { i } | > 0$ in (a3) gives that $\lambda \in G _ { i } ( A )$.
In the same paper, Gershgorin also established the following interesting result: If the $n$ discs $G _ { i } ( A )$ of (a2) consist of two non-empty disjoint sets $S$ and $T$, where $S$ consists of the union of, say, $k$ discs and $T$ consists of the union of the remaining $n - k$ discs, then $S$ contains exactly $k$ eigenvalues (counting multiplicities) of $A$, while $T$ contains exactly $n - k$ eigenvalues of $T$. (The proof of this depends on the fact that the zeros of the characteristic polynomial $p _ { n } ( z )$ vary continuously with the entries $a_{i,\,j}$ of $A$.)
One of the most beautiful results in this area, having to do with the sharpness of the inclusion of (a2), is a result of O. Taussky [a2], which depends on the following use of directed graphs (cf. also Graph, oriented). Given a complex $( n \times n )$-matrix $A = [ a_{i, j} ]$, with $n \geq 2$, let $\{ P _ { i } \} _ { i = 1 } ^ { n }$ be $n$ distinct points, called vertices, in the plane. Then, for each $a _ { i , j } \neq 0$, let $\overset{\rightharpoonup} { P _ { i } P _ { j } }$ denote an arc from vertex $i$ to vertex $j$. The collection of all these arcs defines the directed graph of $A$. Then the matrix $A = [ a_{i, j} ]$, with $n \geq 2$, is said to be irreducible if, given any distinct vertices $i$ and $j$, there is a sequence of abutting arcs from $i$ to $j$, i.e.,
\begin{equation*} \overrightarrow{ P _ { i } P _ { \text{l}_1 } } , \overrightarrow{ P _ { \text{l}_1 } P _ { \text{l}_2 } } , \dots , \overrightarrow{ P _ { \text{l}_m } P _ { \text{l}_{m+1} } }, \end{equation*}
where $\text{l} _ { m + 1 } = j $.
Taussky's theorem is this. Let $A = [ a_{i, j} ]$ be any irreducible complex $( n \times n )$-matrix, with $n \geq 2$. If $\lambda$ is an eigenvalue of $A$ which lies on the boundary of the union of the Gershgorin discs of (a2), then $\lambda$ lies on the boundary of each Gershgorin circle, i.e., from (a1) it follows that
\begin{equation*} | \lambda - a _ { i , i} | = r _ { i } ( A ) \text { for each } 1 \leq i \leq n. \end{equation*}
Next, there is related work of A. Brauer [a3] on estimating the eigenvalues of a complex $( n \times n )$-matrix ($n \geq 2$), which uses Cassini ovals instead of discs. For any integers $i$ and $j$ ($1 \leq i , j \leq n$) with $i \neq j$, the $( i , j )$th Cassini oval is defined by (cf. also Cassini oval)
\begin{equation} \tag{a4} K _ {i ,\, j } ( A ) : = \end{equation}
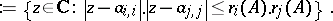 |
Then Brauer's theorem is that, for any eigenvalue $\lambda$ of $A$, there exist $i$ and $j$, with $i \neq j$, such that $\lambda \in K _ { i ,\, j } ( A )$, and this now gives the associated eigenvalue inclusion
\begin{equation} \tag{a5} \sigma ( A ) \subseteq \cup _ { i , j = 1 \atop i \neq j } ^ { n } K _ { i , j } ( A ). \end{equation}
Note that there are now $n ( n - 1 ) / 2$ such Cassini ovals in (a5), as opposed to the $n$ Gershgorin discs in (a2). But it is equally important to note that the eigenvalue inclusions of (a2) and (a5) use the exact same data from the matrix $A = [ a_{i, j} ]$, i.e., $\{ a_{i , i} \} _ { i = 1 } ^ { n }$ and $\{ r _ { i } ( A ) \} _ { i = 1 } ^ { n }$. So, which of the eigenvalue inclusions of (a2) and (a5) is smaller and hence better? It turns out that
\begin{equation} \tag{a6} \bigcup _ { i , j = 1 \atop i \neq j } ^ { n } K _ { i ,\, j} ( A ) \subseteq \bigcup _ { i = 1 } ^ { n } G _ { i } ( A ), \end{equation}
for any complex $( n \times n )$-matrix $A$, so that the Cassini ovals are always at least as good as the Gershgorin discs. (The result (a6) was known to Brauer, but was somehow neglected in the literature.)
Finally, as both eigenvalue inclusions (a2) and (a5) depend only on the row sums $r _ { i } ( A )$, it is evident that these inclusions apply not to just the single matrix $A$, but to a whole class of $( n \times n )$-matrices, namely,
\begin{equation*} \Omega ( A ) : = \end{equation*}
\begin{equation*} : = \{ B = [ b _ { i , j } ] : b _ { i , i } = a _ { i , i } , \text { and } r _ { i } ( B ) = r _ { i } ( A ) , 1 \leq i \leq n \}. \end{equation*}
Thus,
\begin{equation*} \sigma ( B ) \subseteq \cup _ { i , j = 1 \atop i \neq j } ^ { n } K _ { i ,\, j } ( A ) \subseteq \cup _ { i = 1 } ^ { n } G _ { i } ( A ) \end{equation*}
for each $B$ in $\Omega ( A )$. Then, if $\sigma ( \Omega ( A ) )$ denotes the set of all eigenvalues of all $B$ in $\Omega ( A )$, it follows that
\begin{equation} \tag{a7} \sigma ( \Omega ( A ) ) \subseteq \cup _ { i , j = 1 \atop j \neq j } ^ { n } K _ { i,\, j } ( A ) \subseteq \cup _ { i = 1 } ^ { n } G _ { i } ( A ). \end{equation}
How sharp is the first inclusion of (a7)? It was shown in 1999 by R.S. Varga and A. Krautstengl [a4] that
\begin{equation} \tag{a8} \sigma ( \Omega ( A ) ) = \left\{ \begin{array} { c c } { \text { boundary of } K _ { 1,2 } ( A ) } & { n = 2; } \\ { \cup _ { i ,\, j = 1 , i \neq j } ^ { n } K _ { i ,\, j } ( A ) } & { n \geq 3. } \end{array} \right. \end{equation}
Thus, for $n \geq 3$, it can be said that the Cassini ovals give "perfect" results.
Gershgorin's discs and Brauer's Cassini ovals are mentioned in [a5], [a6]. A more detailed treatment of these topics can be found in [a7].
References
| [a1] | S. Gerschgorin, "Ueber die Abgrenzung der Eigenwerte einer Matrix" Izv. Akad. Nauk. SSSR Ser. Mat. , 1 (1931) pp. 749–754 |
| [a2] | O. Taussky, "Bounds for the characteristic roots of matrices" Duke Math. J. , 15 (1948) pp. 1043–1044 |
| [a3] | A. Brauer, "Limits for the characteristic roots of a matrix" Duke Math. J. , 13 (1946) pp. 387–395 |
| [a4] | R.S. Varga, A. Krautstengl, "On Geršgorin-type problems and ovals of Cassini" Electron. Trans. Numer. Anal. , 8 (1999) pp. 15–20 |
| [a5] | R.S. Varga, "Matrix iterative analysis" , Springer (2000) (Edition: Second) |
| [a6] | R.A. Horn, C.R. Johnson, "Matrix analysis" , Cambridge Univ. Press (1985) |
| [a7] | R.S. Varga, "Geršgorin and his circles" , Springer (to appear) |
Gershgorin theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Gershgorin_theorem&oldid=50639