Cassini oval
A plane algebraic curve of order four whose equation in Cartesian coordinates has the form:
$$(x^2+y^2)^2-2c^2(x^2-y^2)=a^4-c^4.$$

Figure: c020700a

Figure: c020700b
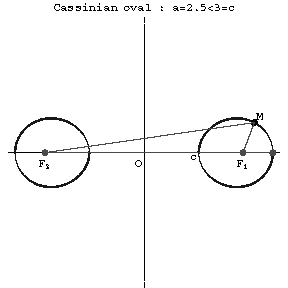
Figure: c020700c
A Cassini oval is the set of points (see Fig.) such that the product of the distances from each point to two given points $F_2=(-c,0)$ and $F_1=(c,0)$ (the foci) is constant. When $a\geq c\sqrt2$ the Cassini oval is a convex curve; when $c<a<c\sqrt2$ it is a curve with "waists" (concave parts); when $a=c$ it is a Bernoulli lemniscate; and when $a<c$ it consists of two components. Cassini ovals are related to lemniscates. Cassini ovals were studied by G. Cassini (17th century) in his attempts to determine the Earth's orbit.
Comments
A Cassini oval is also called a Cassinian oval.
References
| [1] | A.A. Savelov, "Planar curves" , Moscow (1960) (In Russian) |
| [a1] | J.D. Lawrence, "A catalog of special plane curves" , Dover, reprint (1972) MR1572089 Zbl 0257.50002 |
| [a2] | J.W. Bruce, P.J. Giblin, "Curves and singularities: a geometrical introduction to singularity theory" , Cambridge Univ. Press (1984) MR1541053 Zbl 0534.58008 |
Cassini oval. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Cassini_oval&oldid=53342