Formal group
An algebraic analogue of the concept of a local Lie group (cf. Lie group, local). The theory of formal groups has numerous applications in algebraic geometry, class field theory and cobordism theory.
A formal group over a field  is a group object in the category of connected affine formal schemes over
is a group object in the category of connected affine formal schemes over 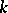 (see [1], [4], [6], [7]). Let
(see [1], [4], [6], [7]). Let 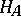 be the functor that associates with an algebra
be the functor that associates with an algebra 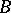 the set of algebra homomorphism
the set of algebra homomorphism 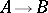 from some Noetherian commutative local
from some Noetherian commutative local 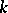 -algebra
-algebra 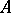 with maximal ideal
with maximal ideal 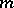 and field of residues
and field of residues 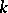 , complete in the
, complete in the 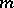 -adic topology, such that the homomorphisms map
-adic topology, such that the homomorphisms map 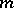 into the set
into the set 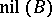 of nilpotent elements of
of nilpotent elements of 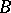 . Then a connected affine formal scheme is a covariant functor
. Then a connected affine formal scheme is a covariant functor 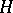 from the category of finite-dimensional commutative
from the category of finite-dimensional commutative 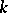 -algebras
-algebras 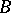 into the category of sets that is isomorphic to an
into the category of sets that is isomorphic to an 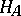 . That
. That 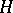 is a group object means that there is a group structure given on all the sets
is a group object means that there is a group structure given on all the sets 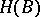 such that for every
such that for every 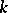 -algebra homomorphism
-algebra homomorphism 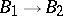 the corresponding mapping
the corresponding mapping 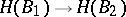 is a group homomorphism. If all the groups
is a group homomorphism. If all the groups  are commutative, then the formal group
are commutative, then the formal group 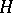 is said to be commutative. Every connected group scheme
is said to be commutative. Every connected group scheme 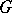 over
over 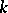 defines a formal group
defines a formal group 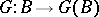 . Here one can take as
. Here one can take as  the completion of the local ring of
the completion of the local ring of 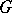 at the unit element.
at the unit element.
If 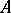 is the ring
is the ring 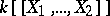 of formal power series in
of formal power series in  variables over
variables over 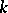 , then
, then 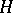 is called an
is called an  -dimensional formal Lie group. For a connected algebraic group
-dimensional formal Lie group. For a connected algebraic group 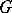 over
over 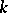 ,
, 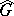 is a formal Lie group. A formal Lie group
is a formal Lie group. A formal Lie group 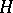 is isomorphic, as a functor in the category of sets, to the functor
is isomorphic, as a functor in the category of sets, to the functor 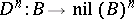 that associates with an algebra
that associates with an algebra 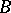 the
the  -fold Cartesian product of its nil radical
-fold Cartesian product of its nil radical  with itself. The group structure on the sets
with itself. The group structure on the sets 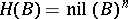 is given by a formal group law — a collection of
is given by a formal group law — a collection of  formal power series in
formal power series in 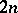 variables
variables 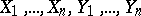 :
:
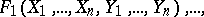 |
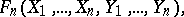 |
satisfying the following conditions:
 |
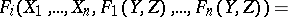 |
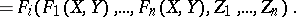 |
Here 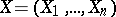 ,
, 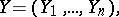
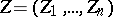 ,
,  . This group law on the sets
. This group law on the sets 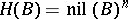 is given by the formulas
is given by the formulas
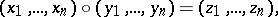 |
where 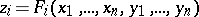 ; because
; because  and
and  are nilpotent, all except a finite number of terms of the series are zero. Every formal group law gives group structures on
are nilpotent, all except a finite number of terms of the series are zero. Every formal group law gives group structures on 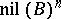 by means of
by means of
and converts the functor 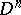 into a formal Lie group. The concept of a formal group law, and thus of a formal Lie group, can be generalized to the case of arbitrary commutative ground rings (see [2], [5]). Sometimes by a formal group one means just a formal Lie group or even a formal group law.
into a formal Lie group. The concept of a formal group law, and thus of a formal Lie group, can be generalized to the case of arbitrary commutative ground rings (see [2], [5]). Sometimes by a formal group one means just a formal Lie group or even a formal group law.
Just as for local Lie groups (cf. Lie group, local) one can define the Lie algebra of a formal Lie group. Over fields 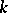 of characteristic 0 the correspondence between a formal Lie group and its Lie algebra defines an equivalence of the respective categories. In characteristic
of characteristic 0 the correspondence between a formal Lie group and its Lie algebra defines an equivalence of the respective categories. In characteristic 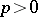 the situation is more complicated. Thus, over an algebraically closed field (for
the situation is more complicated. Thus, over an algebraically closed field (for 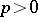 ) there is a countable number of pairwise non-isomorphic one-dimensional commutative formal Lie groups [1], while all one-dimensional Lie algebras are isomorphic [3]. Over perfect fields of finite characteristic, commutative formal Lie groups are classified by means of Dieudonné modules (see [1], [6]).
) there is a countable number of pairwise non-isomorphic one-dimensional commutative formal Lie groups [1], while all one-dimensional Lie algebras are isomorphic [3]. Over perfect fields of finite characteristic, commutative formal Lie groups are classified by means of Dieudonné modules (see [1], [6]).
The theory of formal groups over fields can be generalized to the case of arbitrary formal ground schemes [7].
References
| [1] | Yu.I. Manin, "The theory of commutative formal groups over fields of finite characteristic" Russian Math. Surveys , 18 (1963) pp. 1–80 Uspekhi Mat. Nauk , 18 : 6 (1963) pp. 3–90 |
| [2] | R.E. Stong, "Notes on cobordism theory" , Princeton Univ. Press (1968) |
| [3] | J.-P. Serre, "Lie algebras and Lie groups" , Benjamin (1965) (Translated from French) |
| [4] | R. Hartshorne, "Algebraic geometry" , Springer (1977) |
| [5] | M. Lazard, "Commutative formal groups" , Springer (1975) |
| [6] | J.-M. Fontaine, "Groupes  -divisibles sur les corps locaux" Astérique , 47–48 (1977) -divisibles sur les corps locaux" Astérique , 47–48 (1977) |
| [7] | B. Mazur, J.T. Tate, "Canonical height pairings via biextensions" J.T. Tate (ed.) M. Artin (ed.) , Arithmetic and geometry , 1 , Birkhäuser (1983) pp. 195–237 |
Comments
A universal formal group law (for  -dimensional formal group laws) is an
-dimensional formal group laws) is an  -dimensional formal group law
-dimensional formal group law 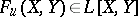 ,
, 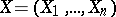 ,
, 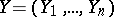 such that for every
such that for every  -dimensional formal group law
-dimensional formal group law 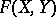 over a ring
over a ring 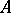 there is a unique homomorphism of rings
there is a unique homomorphism of rings 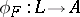 such that
such that 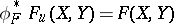 . Here
. Here 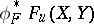 denotes the result of applying
denotes the result of applying 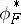 to the coefficients of the
to the coefficients of the  power series
power series 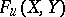 . Universal formal group laws exist and are unique in the sense that if
. Universal formal group laws exist and are unique in the sense that if 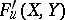 over
over 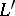 is another one, then there exists a ring isomorphism
is another one, then there exists a ring isomorphism 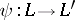 such that
such that 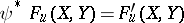 .
.
For commutative formal group laws explicit formulas are available for the construction of universal formal group laws, cf. [a3]. The underlying ring 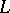 is a ring of polynomials in infinitely many indeterminates (Lazard's theorem).
is a ring of polynomials in infinitely many indeterminates (Lazard's theorem).
A homomorphism of formal group laws 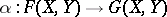 ,
, 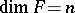 ,
, 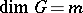 , is an
, is an 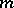 -tuple of power series in
-tuple of power series in  -variables
-variables 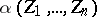 ,
, 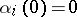 , such that
, such that 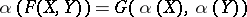 . The homomorphism is an isomorphism if there exists an inverse homomorphism
. The homomorphism is an isomorphism if there exists an inverse homomorphism 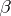 such that
such that 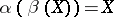 , and it is a strict isomorphism of formal group laws if
, and it is a strict isomorphism of formal group laws if 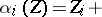 (higher order terms).
(higher order terms).
Let 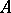 be a ring of characteristic zero, i.e. the homomorphism of rings
be a ring of characteristic zero, i.e. the homomorphism of rings 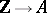 which sends
which sends 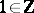 to the unit element in
to the unit element in 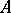 is injective. Then
is injective. Then 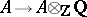 is injective. Over
is injective. Over 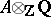 all commutative formal group laws are strictly isomorphic and hence isomorphic to the additive formal group law
all commutative formal group laws are strictly isomorphic and hence isomorphic to the additive formal group law
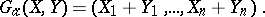 |
It follows that for every commutative formal group law 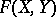 over
over 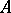 there exists a unique
there exists a unique  -tuple of power series
-tuple of power series 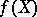 ,
, 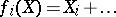 with coefficients in
with coefficients in 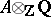 such that
such that
 |
where 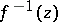 is the "inverse function" to
is the "inverse function" to 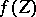 , i.e.
, i.e. 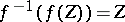 . This
. This 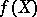 is called the logarithm of the group law
is called the logarithm of the group law 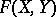 .
.
The formal group law of complex cobordism is a universal one-dimensional formal group law (Quillen's theorem) and its logarithm is given by Mishchenko's formula
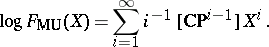 |
Combined with the explicit construction of a one-dimensional universal group law these facts yield useful information on the generators of the complex cobordism ring 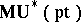 . Cf. Cobordism for more details.
. Cf. Cobordism for more details.
Let 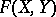 be an
be an  -dimensional group law over
-dimensional group law over 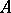 . A curve over
. A curve over 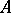 in
in 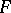 is an
is an  -tuple of power series
-tuple of power series 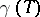 in one variable such that
in one variable such that 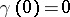 . Two curves can be added by
. Two curves can be added by 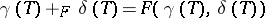 . The set of curves is given the natural power series topology and there results a commutative topological group
. The set of curves is given the natural power series topology and there results a commutative topological group 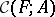 . The group
. The group  admits a number of operators
admits a number of operators 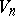 ,
, 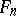 ,
, 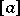 ,
, 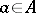 , defined as follows:
, defined as follows:
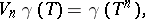 |
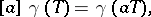 |
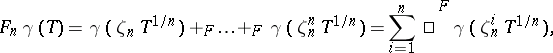 |
where 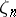 is a primitive
is a primitive  -th root of unity. There are a number of relations between these operators and they combine to define a (non-commutative) ring
-th root of unity. There are a number of relations between these operators and they combine to define a (non-commutative) ring 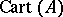 , which generalizes the Dieudonné ring, cf. Witt vector for the latter. Cartier's second and third theorems on formal group laws say that the
, which generalizes the Dieudonné ring, cf. Witt vector for the latter. Cartier's second and third theorems on formal group laws say that the 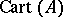 modules
modules  classify formal groups and they characterize which groups occur as
classify formal groups and they characterize which groups occur as  's. This is the covariant classification of commutative formal groups in contrast with the earlier contravariant classification of commutative formal groups over perfect fields by Dieudonné modules.
's. This is the covariant classification of commutative formal groups in contrast with the earlier contravariant classification of commutative formal groups over perfect fields by Dieudonné modules.
Let 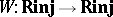 be the functor of Witt vectors (cf. Witt vector). Let
be the functor of Witt vectors (cf. Witt vector). Let 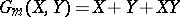 be the (one-dimensional) multiplicative formal group law over
be the (one-dimensional) multiplicative formal group law over 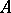 . Then
. Then 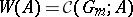 . Cartier's first theorem for formal group laws says that the functor
. Cartier's first theorem for formal group laws says that the functor 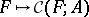 is representable. More precisely, let
is representable. More precisely, let 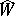 be the (infinite-dimensional) formal group law given by the addition formulas of the Witt vectors and let
be the (infinite-dimensional) formal group law given by the addition formulas of the Witt vectors and let 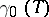 be the curve
be the curve 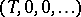 . Then for every formal group law
. Then for every formal group law 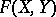 and curve
and curve 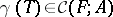 there is unique homomorphism of formal group laws
there is unique homomorphism of formal group laws 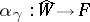 such that
such that 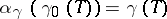 .
.
There exists a Pontryagin-type duality between commutative formal groups and commutative affine (algebraic) groups over a field 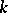 , called Cartier duality. Cf. [a3], [a4] for more details. Correspondingly, Dieudonné modules are also important in the classification of commutative affine (algebraic) groups. Essentially, Cartier duality comes from the "duality" between algebras and co-algebras; cf. Co-algebra.
, called Cartier duality. Cf. [a3], [a4] for more details. Correspondingly, Dieudonné modules are also important in the classification of commutative affine (algebraic) groups. Essentially, Cartier duality comes from the "duality" between algebras and co-algebras; cf. Co-algebra.
Let 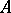 be a discrete valuation ring with finite residue field
be a discrete valuation ring with finite residue field  and maximal ideal
and maximal ideal 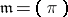 . The Lubin–Tate formal group law associated to
. The Lubin–Tate formal group law associated to 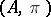 is defined by the logarithm
is defined by the logarithm
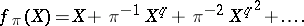 |
Then 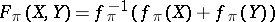 has its coefficients in
has its coefficients in 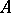 . These formal group laws are in a sense formal
. These formal group laws are in a sense formal 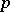 -adic analogues of elliptic curves with complex multiplication in that they have maximally large endomorphism rings. They are also analogues in the role they play vis à vis the class field theory of
-adic analogues of elliptic curves with complex multiplication in that they have maximally large endomorphism rings. They are also analogues in the role they play vis à vis the class field theory of 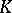 , the quotient field of
, the quotient field of 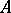 . Indeed, let
. Indeed, let  be the set
be the set 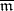 with the addition
with the addition 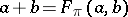 . Here
. Here 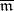 is the maximal ideal of the ring of integers of an algebraic closure of
is the maximal ideal of the ring of integers of an algebraic closure of 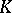 . Then a maximal Abelian totally ramified extension of
. Then a maximal Abelian totally ramified extension of 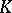 is generated by the torsion elements of
is generated by the torsion elements of 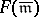 ; cf. [a3], [a5] for more details.
; cf. [a3], [a5] for more details.
Formal groups also are an important tool in algebraic geometry, especially in the theory of Abelian varieties. This holds even more so for a generalization: 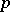 -divisible groups; cf.
-divisible groups; cf. 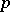 -divisible group.
-divisible group.
Lazard's theorem on one-dimensional formal group laws says that all one-dimensional formal group laws over a ring without nilpotents are commutative.
Let 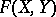 be a one-dimensional formal group law. Define inductively
be a one-dimensional formal group law. Define inductively 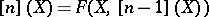 ,
, 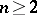 ,
, 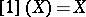 . Let
. Let 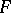 be defined over a field
be defined over a field 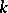 of characteristic
of characteristic 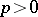 . Then
. Then 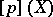 is necessarily of the form
is necessarily of the form 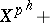 (higher degree terms) or is equal to zero. The positive integer
(higher degree terms) or is equal to zero. The positive integer 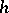 is called the height of
is called the height of 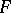 ; if
; if 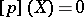 , the height of
, the height of 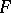 is taken to be
is taken to be 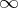 . Over an algebraically closed field of characteristic
. Over an algebraically closed field of characteristic 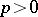 the one-dimensional formal group laws are classified by their heights, and all heights
the one-dimensional formal group laws are classified by their heights, and all heights 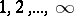 occur.
occur.
Let 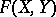 be a one-dimensional formal group law over a ring
be a one-dimensional formal group law over a ring 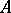 in which every prime number except
in which every prime number except  is invertible, e.g.
is invertible, e.g. 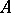 is the ring of integers of a local field of residue characteristic
is the ring of integers of a local field of residue characteristic 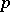 or
or 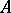 is a field of characteristic
is a field of characteristic 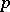 . Assume for the moment that
. Assume for the moment that 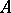 is of characteristic zero and let
is of characteristic zero and let
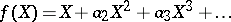 |
be the logarithm of 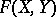 . Then
. Then 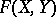 is strictly isomorphic over
is strictly isomorphic over 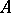 to the formal group law
to the formal group law 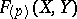 whose logarithm is equal to
whose logarithm is equal to
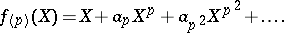 |
The result extends to the case that 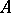 is not of characteristic zero and to more-dimensional commutative formal group laws.
is not of characteristic zero and to more-dimensional commutative formal group laws. 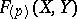 is called the
is called the 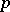 -typification of
-typification of 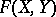 .
.
References
| [a1] | J.T. Tate, "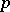 -divisible groups" T.A. Springer (ed.) et al. (ed.) , Proc. Conf. local fields (Driebergen, 1966) , Springer (1967) pp. 158–183 -divisible groups" T.A. Springer (ed.) et al. (ed.) , Proc. Conf. local fields (Driebergen, 1966) , Springer (1967) pp. 158–183 |
| [a2] | J.-P. Serre, "Groupes 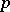 -divisible (d' après J. Tate)" Sem. Bourbaki , 19, Exp. 318 (1966–1967) -divisible (d' après J. Tate)" Sem. Bourbaki , 19, Exp. 318 (1966–1967) |
| [a3] | M. Hazewinkel, "Formal groups and applications" , Acad. Press (1978) |
| [a4] | M. Demazure, P. Gabriel, "Groupes algébriques" , 1 , Masson & North-Holland (1970) |
| [a5] | J. Lubin, J. Tate, "Formal complex multiplication in local fields" Ann. of Math. , 81 (1965) pp. 380–387 |
Formal group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Formal_group&oldid=17665