Difference between revisions of "Finite group"
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
m (Wikilink) |
||
| Line 11: | Line 11: | ||
{{TEX|done}} | {{TEX|done}} | ||
| − | A group with finitely many elements. The number of elements is called the order of the group. Historically, many concepts in abstract group theory have had their origin in the theory of finite groups. | + | A [[group]] with finitely many elements. The number of elements is called the order of the group. Historically, many concepts in abstract group theory have had their origin in the theory of finite groups. |
It is usually said that the aim of finite group theory is to describe the groups of given order up to isomorphism. This is only partly true. A naïve approach based on a wish to classify all groups is doomed to failure. For example, the compilation of a list of all non-isomorphic groups of the comparatively small order 1024 would constitute a difficult task for the best modern computers. In general, the classification of finite $ p $- | It is usually said that the aim of finite group theory is to describe the groups of given order up to isomorphism. This is only partly true. A naïve approach based on a wish to classify all groups is doomed to failure. For example, the compilation of a list of all non-isomorphic groups of the comparatively small order 1024 would constitute a difficult task for the best modern computers. In general, the classification of finite $ p $- | ||
Latest revision as of 09:10, 4 July 2020
A group with finitely many elements. The number of elements is called the order of the group. Historically, many concepts in abstract group theory have had their origin in the theory of finite groups.
It is usually said that the aim of finite group theory is to describe the groups of given order up to isomorphism. This is only partly true. A naïve approach based on a wish to classify all groups is doomed to failure. For example, the compilation of a list of all non-isomorphic groups of the comparatively small order 1024 would constitute a difficult task for the best modern computers. In general, the classification of finite $ p $- groups (groups of order $ p ^ {n} $, $ p $ a prime number) is a "wild" problem. On the other hand, there do exist some extremal classes of groups, playing a central role in the theory, for which the classification problem (enumeration up to isomorphism) is either solved or is a perfectly reasonable objective.
Thus there is a complete theory of finite Abelian groups (see Abelian group) and various classes of finite $ p $- groups (regular, free of exponent $ p $, of maximal class, those given by generators and the least possible number of relations) allow of a qualitative description. The description of finite groups of integral invertible matrices is an example of an important classification problem; it has been solved only for small orders of the matrices.
During the formative period in the theory of finite groups, which is associated with the names of A.L. Cauchy, J.L. Lagrange, C.F. Gauss, N.H. Abel, and later E. Galois, finite groups were studied almost entirely in the form of permutation groups (whence the unsuccessful well-established term substitution group, cf. Permutation group), and this point of view is still fruitful today. For example, if an abstract finite group $ G $ can be realized as a multiply-transitive permutation group (that is, as a suitable subgroup of a symmetric group $ S _ {m} $), then in a number of cases $ G $ is uniquely determined up to isomorphism. Classification results for simple $ 2 $- transitive groups constitute a rich section of finite group theory, whose foundations were laid more than a hundred years ago by C. Jordan. The computational methods in the theory of permutation groups, developed in recent years, have been called into existence partly by the requirements of combinatorics, graph theory, coding theory, and the need to check various conjectures.
The theory of linear representations of finite groups, developed at the beginning of the 20th century by G. Frobenius, W. Burnside, I. Schur, and others (see Finite group, representation of a), provided a powerful tool for investigating abstract groups, and served as a prototype for the analogous representation theory of Lie groups, and later of other algebraic systems. The formulation of properties of groups and their representations in terms of the theory of characters is one manifestation of the mutual relationships between the various branches of algebra. Representations of finite groups over commutative rings and fields of non-zero characteristic, intensively investigated by R. Brauer and others (see [2]), have been exploited to yield many deep results.
Extensions of finite groups are studied using the cohomology theory of groups (see Cohomology of groups), which is also of independent interest.
The almost obvious idea that properties of a finite group $ G $ must to some extent be arithmetical and depend on the canonical prime factorization $ | G | = p _ {1} ^ {n _ {1} } \dots p _ {k} ^ {n _ {k} } $ of its order, is given precise form in the Sylow theorems on the existence and conjugacy of subgroups of order $ p _ {i} ^ {n _ {i} } $. If $ | G | = mn $, where $ n $ and $ m $ are relatively prime natural numbers, then a subgroup of order $ n $, called a Hall subgroup, need not, in general, exist. However, for the large class of solvable groups, Hall subgroups exist and fully inherit the properties of Sylow subgroups. The solvability of groups of order $ p ^ {a} q ^ {b} $( where $ p $ and $ q $ are prime numbers), discovered by Burnside, is a typical example of an arithmetical property. The solvability of groups of odd order, established many years later by J. Thompson and W. Feit (see Burnside problem, 1), is an achievement which has given finite group theory a radically new orientation. The existence of involutions (elements of order 2) in non-solvable groups — an alternative formulation of the Feit–Thompson theorem — and the expression of properties of simple groups in terms of centralizers of involutions have formed one of the principal directions of research in finite group theory (the realization of Brauer's programme).
In the roaring period 1961–1981, marked by constant activity of algebraists in various countries, one of the most remarkable achievements in the history of mathematics was made: the classification of the finite simple groups (cf. Simple finite group). Regrettably, a drawback of this classification is the fact that until now it has not been verified, because of the absence of one integral text and the exceptional complexity of the structure of the reasoning used. Therefore the task of rendering individual parts of the proof more transparent has not faded away, and the branch of the theory occupied with the finite simple groups continues to be an active one. All kinds of consequences of the classification are of interest (e.g., the description of all $ 2 $- transitive groups), although many mathematicians call results of this kind conditional, out of precaution.
Parallel with the classification direction, an intensive study was made of invariants of the finite linear groups and of properties of representations. Especially fruitful has been the work concerning the description of all complex characters of the finite simple groups of Lie type. Substantial progress was made in this case, a symbol of this being the theory of Deligne–Lusztig, which was brought about by combining methods of algebraic geometry and the theory of algebraic groups. Nowadays, this theory is one of the most splendid parts of algebra, on the interface between the theory of finite groups and its applications in most varied branches of mathematics.
References
| [1] | F. Klein, "Development of mathematics in the 19th century" , Math. Sci. Press (1979) (Translated from German) MR0529278 MR0549187 Zbl 0411.01009 |
| [2] | C.W. Curtis, I. Reiner, "Representation theory of finite groups and associative algebras" , Interscience (1962) MR0144979 Zbl 0131.25601 |
| [3] | M.I. Kargapolov, J.I. [Yu.I. Merzlyakov] Merzljakov, "Fundamentals of the theory of groups" , Springer (1979) (Translated from Russian) MR0551207 Zbl 0549.20001 |
| [4] | A.I. Kostrikin, "Finite groups" Itogi Nauk. Algebra 1964 (1966) pp. 7–46 (In Russian) MR0210773 Zbl 0830.00003 Zbl 0637.20004 Zbl 0601.17004 Zbl 0606.20008 Zbl 0547.17004 Zbl 0496.20010 Zbl 0137.25601 |
| [5] | S.A. Chunikhin, L.A. Shemetkov, "Finite groups" Itogi Nauk. Algebra. Topol. Geom. 1969 (1971) pp. 7–70 (In Russian) MR0790342 MR0248209 Zbl 0239.20028 Zbl 0224.20017 Zbl 0224.20006 |
| [6] | V.D. Mazurov, "Finite groups" Itogi Nauk. Algebra. Topol. Geom. , 14 (1976) pp. 5–56 (In Russian) MR0506806 Zbl 0444.20011 |
| [7] | A. Speiser, "Die Theorie der Gruppen von endlicher Ordnung" , Birkhäuser (1956) MR0079585 Zbl 0070.25601 |
| [8] | H. Wielandt, "Finite permutation groups" , Acad. Press (1968) (Translated from German) MR1533942 MR0183775 Zbl 0138.02501 |
| [9] | B. Huppert, "Endliche Gruppen" , 1 , Springer (1967) MR0224703 Zbl 0217.07201 |
| [10] | D. Gorenstein, "Finite groups" , Harper & Row (1968) MR0231903 Zbl 0185.05701 |
| [11] | I.M. Isaacs, "Character theory of finite groups" , Acad. Press (1976) MR0460423 Zbl 0337.20005 |
| [12] | M. Aschbacher, "Finite group theory" , Cambridge Univ. Press (1986) MR0895134 Zbl 0583.20001 |
| [13] | D. Gorenstein, "Finite simple groups. An introduction to their classification" , Plenum (1982) MR0698782 Zbl 0483.20008 |
Comments
In order to appreciate the difficulty of a naïve approach, cf. the classification of the 267 groups of order 64 in [a1].
The finite simple groups have been classified only recently (as mentioned in the article above; they include the Chevalley groups (plus twisted types), the alternating groups of degrees at least 5 and the 26 so-called sporadic groups; for details see Simple finite group). See [13] for a detailed assessment as to 1982. As a consequence all permutation groups which are $ 2 $- transitive or primitive of rank 3 (i.e., have 3 orbits on the set of all unordered pairs) have been determined, cf. [a5]. For further consequences see [a6], [a2].
Burnside's result on the solvability of groups of order $ p ^ {a} q ^ {p} $ has been recently proved by D.M. Goldschmidt and H. Matsuyama without using character theory (cf. Character of a group, and [a4]).
References
| [a1] | M. Hall, "The groups of order 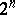 ( (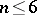 )" , Macmillan (1964) )" , Macmillan (1964) |
| [a2] | W.M. Kantor, "Some consequences of the classification of finite simple groups" Contempory Math. , 45 (1985) pp. 159–173 MR0822238 Zbl 0594.20008 |
| [a3] | N. Blackburn, B. Huppert, "Finite groups" , 1–2 , Springer (1981–1982) MR2441064 MR2382539 MR1346020 MR0662826 MR0650245 MR0190229 Zbl 1141.20001 Zbl 0891.20015 Zbl 0939.94515 Zbl 0951.94544 Zbl 0514.20002 Zbl 0477.20001 Zbl 0144.26403 Zbl 0141.02401 |
| [a4] | M. Suzuki, "Group theory" , 1–2 , Springer (1986) MR0815926 Zbl 0586.20001 |
| [a5] | M.W. Liebeck, "The affine permutation groups of rank three" Proc. London Math. Soc. (3) , 54 (1987) pp. 477–516 MR0879395 Zbl 0621.20001 |
| [a6] | W. Feit, "Some consequences of the classification of finite simple groups" , Proc. Symp. Pure Math. , 37 , Amer. Math. Soc. (1980) pp. 175–181 MR0604576 Zbl 0454.20014 |
Finite group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Finite_group&oldid=50883