Differential geometry of manifolds
A branch of differential geometry dealing with various infinitesimal structures (cf. Infinitesimal structure) on a manifold and their connection with the structure of the manifold and its topology.
It became clear in the middle of the 19th century, with the discovery of the non-Euclidean Lobachevskii geometry, the higher-dimensional geometry of Grassmann, and with the development of projective geometry and geometry in the complex domain, that the conventional Euclidean geometry is not the only possible one, and that it is advantageous in mathematics to develop other, non-Euclidean, geometries, irrespective of their relationship with the geometry of physical space.
B. Riemann in 1854 proposed the new, very fruitful, concept of a "manifold" in his course Über die Hypothesen, welche der Geometrie zuGrunde liegen (cf. Riemannian space). This paper was the origin of Riemannian geometry, which is the most important and the most advanced part of the differential geometry of manifolds. Riemann's concept does not merely represent a unified description of a wide class of geometries (including Euclidean geometry and Lobachevskii's non-Euclidean geometry), but has also provided the mathematical apparatus for a geometrical treatment of various problems in mathematical physics and in analysis connected with differential equations. This makes it possible to use various geometrical and topological concepts when solving these problems and has opened new possibilities for the application of geometry to analysis. It is Riemannian geometry which was used by A. Einstein to realize the idea of physical space as a continuum, the properties of which are determined by the distribution of matter. A Riemannian space is the name given to a differentiable manifold 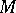 for which on each tangent space
for which on each tangent space 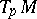 a Euclidean metric
a Euclidean metric 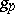 (i.e. a positive-definite scalar product) is given, depending smoothly on the point
(i.e. a positive-definite scalar product) is given, depending smoothly on the point 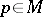 . The presence of the scalar product on the tangent space
. The presence of the scalar product on the tangent space 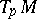 of the Riemannian space
of the Riemannian space 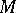 makes it possible to determine, by the formulas of Euclidean geometry, the angle between infinitesimal curves (i.e. vectors in
makes it possible to determine, by the formulas of Euclidean geometry, the angle between infinitesimal curves (i.e. vectors in 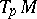 ), the length of an infinitesimal curve, and also the volume of a
), the length of an infinitesimal curve, and also the volume of a 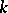 -dimensional parallelepiped in
-dimensional parallelepiped in  and then, by integration, the length of a smooth curve on
and then, by integration, the length of a smooth curve on 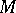 and the volume of a
and the volume of a 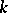 -dimensional submanifold in
-dimensional submanifold in 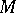 . This in turn permits one to consider various variational problems in the framework of Riemannian geometry and, in particular, to define the concept of a geodesic (or a geodesic line) in a Riemannian space as a curve of minimal length and a minimal surface as a submanifold of minimal volume.
. This in turn permits one to consider various variational problems in the framework of Riemannian geometry and, in particular, to define the concept of a geodesic (or a geodesic line) in a Riemannian space as a curve of minimal length and a minimal surface as a submanifold of minimal volume.
The study of the geodesics of a Riemannian space is one of the main problems of modern (global) Riemannian geometry. Its importance in applications is due to the fact that various dynamical systems in physics are interpreted as uniform motion along the geodesics of some pseudo-Riemannian space. Such systems include, for example, the motions of test bodies (cf. Geodesic hypothesis) in general relativity theory, the propagation of light in a non-homogeneous medium in approximations of geometrical optics, and different systems of classical mechanics. It has been noted that certain important partial differential equations (the equation of motion of an ideal liquid and Einstein's equation of general relativity theory) can be interpreted as equations of geodesics for certain infinite-dimensional Riemannian spaces, which are also known as Hilbert manifolds [5], [12]. These discoveries stimulated the development of the geometry of infinite-dimensional manifolds — global analysis.
A complete integration of the equations of geodesics is possible only in exceptional cases. In this context, an important role is taken by geometrical and topological methods for the qualitative study of the behaviour of geodesics. Of these, the most important one is M. Morse's variational theory of geodesics (cf. Morse theory, [20]).
The generalization of Morse theory to pseudo-Riemannian spaces resulted in the proof of singularity theorems which state that, in general relativity theory, the physical space-time will usually have singularities (incomplete geodesics). The physical interpretation of a singularity is, for example, a "black hole" [7].
The behaviour of geodesics of a Riemannian space is largely determined by its curvature tensor (the Riemann tensor) — a geometrical object characterizing the deviation of the Riemannian from the Euclidean space. Similarly to the Gaussian curvature of a surface, the curvature tensor of a Riemannian space 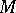 at a point
at a point  , which is a generalization of the Gaussian curvature, determines the properties of the space
, which is a generalization of the Gaussian curvature, determines the properties of the space 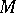 in a neighbourhood of the point
in a neighbourhood of the point  . Moreover, the curvature tensor carries rich information about the global properties of the Riemannian space and its topology, e.g. on the fundamental group; the Betti numbers (cf. Betti number) and the characteristic classes (cf. Characteristic class). The study of the connection between the local properties of the curvature tensor and the global properties of a Riemannian space is one of the principal problems of modern global Riemannian geometry [21].
. Moreover, the curvature tensor carries rich information about the global properties of the Riemannian space and its topology, e.g. on the fundamental group; the Betti numbers (cf. Betti number) and the characteristic classes (cf. Characteristic class). The study of the connection between the local properties of the curvature tensor and the global properties of a Riemannian space is one of the principal problems of modern global Riemannian geometry [21].
Any submanifold 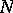 of a Riemannian space
of a Riemannian space 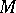 inherits from
inherits from 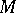 the structure of a Riemannian space. The study of submanifolds of a Riemannian space, as well as the clarification of the problem of the realization of a given Riemannian space
the structure of a Riemannian space. The study of submanifolds of a Riemannian space, as well as the clarification of the problem of the realization of a given Riemannian space 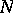 as a submanifold of a given Riemannian space
as a submanifold of a given Riemannian space 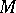 , is the main subject of the geometry of submanifolds (see also Isometric immersion).
, is the main subject of the geometry of submanifolds (see also Isometric immersion).
An important direction in the study of Riemannian spaces, starting with the work of S. Lie and W. Killing, is the study of their groups of isometries (i.e. transformations which preserve the lengths of curves); these are, invariably, Lie groups. Many important Riemannian spaces 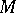 have a fairly rich group of isometries, and the presence of such a group is very helpful in the study of a large number of geometrical problems. The presence of a transitive group of isometries makes it possible to reduce the study of the geometry and topology of the space
have a fairly rich group of isometries, and the presence of such a group is very helpful in the study of a large number of geometrical problems. The presence of a transitive group of isometries makes it possible to reduce the study of the geometry and topology of the space 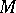 to problems of the theory of Lie groups (cf. Homogeneous space).
to problems of the theory of Lie groups (cf. Homogeneous space).
The description of the (connected) group of isometries 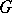 of a Riemannian space
of a Riemannian space 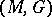 is reduced to the description of the Lie algebra of infinitesimal motions (or Killing vectors, cf. Killing vector), which are defined as velocity fields of one-parameter subgroups of
is reduced to the description of the Lie algebra of infinitesimal motions (or Killing vectors, cf. Killing vector), which are defined as velocity fields of one-parameter subgroups of 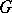 . Qualitative geometrical methods of studying Killing fields, and the clarification of the connection between these fields and the geometrical properties of space, mainly the properties of its curvature tensor, play an important role. Thus it can be proved, for example, that Killing fields do not exist in a compact Riemannian space with a negative Ricci curvature; an integral curve of a Killing field passing through an extremal point of its length is a geodesic [16]; the behaviour of the Killing field
. Qualitative geometrical methods of studying Killing fields, and the clarification of the connection between these fields and the geometrical properties of space, mainly the properties of its curvature tensor, play an important role. Thus it can be proved, for example, that Killing fields do not exist in a compact Riemannian space with a negative Ricci curvature; an integral curve of a Killing field passing through an extremal point of its length is a geodesic [16]; the behaviour of the Killing field  in a neighbourhood of its stationary points (i.e. points where
in a neighbourhood of its stationary points (i.e. points where 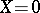 ) determines an important topological invariant of the Riemannian space — to wit, its Pontryagin number [16].
) determines an important topological invariant of the Riemannian space — to wit, its Pontryagin number [16].
Of special interest are Riemannian spaces with a sufficiently large group of isometries. As was noted by H. Helmholtz as early as 1868, and rigorously proved by Lie, an  -dimensional Riemannian space
-dimensional Riemannian space 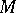 with the largest (with respect to the dimension) group of isometries for a given
with the largest (with respect to the dimension) group of isometries for a given  , is a space of constant curvature (e.g., the Euclidean space
, is a space of constant curvature (e.g., the Euclidean space 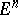 , the Lobachevskii space
, the Lobachevskii space 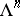 or the spherical Riemannian space
or the spherical Riemannian space 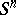 , cf. Constant curvature, space of). Spaces with properties closest to those of spaces of constant curvature are the symmetric spaces (cf. Symmetric space), i.e. Riemannian spaces in which the geodesic symmetry with respect to an arbitrary point is an isometry. These spaces always have a transitive group of isometries and may be classified using the theory of semi-simple Lie algebras [8].
, cf. Constant curvature, space of). Spaces with properties closest to those of spaces of constant curvature are the symmetric spaces (cf. Symmetric space), i.e. Riemannian spaces in which the geodesic symmetry with respect to an arbitrary point is an isometry. These spaces always have a transitive group of isometries and may be classified using the theory of semi-simple Lie algebras [8].
An important role in differential geometry is played by the concept of the covariant derivative 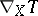 of a tensor field
of a tensor field 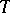 on
on 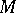 in the direction of the vector
in the direction of the vector 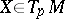 . This concept was introduced by G. Ricci, who used it as starting point in the development of "absolute differential calculus" (cf. Tensor analysis). The apparatus of covariant differentiation proved suitable for obtaining invariants of geometric objects. Thus, the complete system of invariants of a Riemannian metric, found by E. Christoffel and R. Lipschitz, consists of the curvature tensor and its successive covariant derivatives.
. This concept was introduced by G. Ricci, who used it as starting point in the development of "absolute differential calculus" (cf. Tensor analysis). The apparatus of covariant differentiation proved suitable for obtaining invariants of geometric objects. Thus, the complete system of invariants of a Riemannian metric, found by E. Christoffel and R. Lipschitz, consists of the curvature tensor and its successive covariant derivatives.
The concept of the covariant derivative makes it possible to define in a canonical manner a number of differential operators on a Riemannian space, the properties of which are closely connected with the geometry of the space. The most important one is the Laplace–Beltrami operator 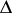 , which was introduced by E. Beltrami and which coincides with the Laplace operator for a Euclidean space. A wide class of linear partial differential equations of the second order can be interpreted, in the framework of pseudo-Riemannian spaces, as equations corresponding to the Laplace–Beltrami operator. This allows one to utilize Riemannian geometry in the study of these equations. The first example of such an approach (for the heat equation) was given by Riemann [1]. Results establishing the connection between the properties of the Laplace–Beltrami operator of a Riemannian space, in particular between its spectrum, and the geometry of the space — its curvature, the number of closed geodesics, etc. — have been obtained [19].
, which was introduced by E. Beltrami and which coincides with the Laplace operator for a Euclidean space. A wide class of linear partial differential equations of the second order can be interpreted, in the framework of pseudo-Riemannian spaces, as equations corresponding to the Laplace–Beltrami operator. This allows one to utilize Riemannian geometry in the study of these equations. The first example of such an approach (for the heat equation) was given by Riemann [1]. Results establishing the connection between the properties of the Laplace–Beltrami operator of a Riemannian space, in particular between its spectrum, and the geometry of the space — its curvature, the number of closed geodesics, etc. — have been obtained [19].
T. Levi-Civita gave a geometric interpretation of the concept of the covariant derivative. He showed that in a Riemannian space it is possible to define in a canonical manner a parallel displacement of tangent vectors (tensors) along curves, while the Ricci operator of covariant differentiation is the operator of infinitesimal parallel displacement (cf. Levi-Civita connection).
In 1926 E. Cartan introduced the concept of a holonomy group as the group 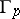 of linear transformations of the tangent space
of linear transformations of the tangent space  of a Riemannian space
of a Riemannian space 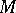 generated by the operators
generated by the operators 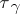 of parallel displacements along all possible loops
of parallel displacements along all possible loops 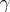 through
through 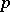 . It was found that the holonomy group is closely connected with the curvature tensor of the space and, for a simply-connected analytic space, is completely defined by the curvature tensor and all its covariant derivatives at a point; on the other hand, it contains certain information on the geometry and topology of the space. Thus, if the holonomy group is known, it is possible to find all parallel fields, and also solve the problem on the possibility of decomposing the Riemannian space into the direct product of two other Riemannian spaces. Using the holonomy group of a symmetric space, the space itself can be constructed and its group of isometries can be determined.
. It was found that the holonomy group is closely connected with the curvature tensor of the space and, for a simply-connected analytic space, is completely defined by the curvature tensor and all its covariant derivatives at a point; on the other hand, it contains certain information on the geometry and topology of the space. Thus, if the holonomy group is known, it is possible to find all parallel fields, and also solve the problem on the possibility of decomposing the Riemannian space into the direct product of two other Riemannian spaces. Using the holonomy group of a symmetric space, the space itself can be constructed and its group of isometries can be determined.
In 1919, while developing the idea of parallel displacement of Levi-Civita and generalizing Riemann's concept of space, H. Weyl considered a space with a linear connection — a manifold with a specified law of parallel displacement of tangent vectors along curves. The concepts of geodesics, curvature tensor and holonomy group are all defined in a space with a linear connection. A Riemannian space is a special case of a space with a linear connection for which the holonomy group is contained in the orthogonal group. If the holonomy group is contained in the group 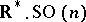 of linear homotheties, the connection is called conformal; in such a case a conformal structure results on the manifold.
of linear homotheties, the connection is called conformal; in such a case a conformal structure results on the manifold.
The development of the ideas of Weyl led to the construction of the modern theory of connections on a manifold, the subject of which are connections (i.e. laws of parallel displacement of fibres along curves in the base) on a given fibre bundle. This theory gave rise, in particular, to the theory of characteristic classes [11], [16]. The concept of a connection plays an important role in modern physics. Various physical fields (in particular, electromagnetic and gravitational fields) may be interpreted as fields of curvature of a connection in a given fibre bundle, in the framework of the Yang–Mills theory. The presence of connections on any physical fibre bundle, i.e. a fibre bundle with physical fields as sections, follows from the physical fact that field characteristics at different points of space-time can be compared (along a curve).
Another generalization of a Riemannian space is a Finsler space, which is defined as a manifold with a Finsler metric. The Lagrangian of a mechanical system is an example of such a metric. Finsler manifolds also appear in optics in a natural way.
A new group-theoretical approach to the foundations of geometry — the so-called "Erlangen programErlangen program" — was proposed by F. Klein in 1872. He proposed that a 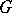 -space — a manifold
-space — a manifold 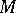 together with a given group
together with a given group 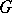 of transformations of it — be the main object of study in geometry.
of transformations of it — be the main object of study in geometry.
According to Klein, the principal task of geometry is to study the invariants of the group of transformations (cf. Erlangen program). While this approach proved to be too narrow — many important Riemannian spaces have a trivial group of isometries — it nevertheless played an important part in the development of the differential geometry of manifolds. It drew attention to the important class of homogeneous spaces (i.e. 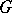 -spaces with a transitive group
-spaces with a transitive group 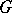 ). The study of the geometry of these spaces is reduced in the Erlangen program to problems of the theory of Lie groups, and has inspired further generalizations of the concept of Riemann. This generalization consisted in the study of the geometry of other (non-Riemannian) infinitesimal structures on a manifold given by a field of specific geometrical quantities. Many such structures were first obtained as invariants of the group of isometries of some homogeneous space.
). The study of the geometry of these spaces is reduced in the Erlangen program to problems of the theory of Lie groups, and has inspired further generalizations of the concept of Riemann. This generalization consisted in the study of the geometry of other (non-Riemannian) infinitesimal structures on a manifold given by a field of specific geometrical quantities. Many such structures were first obtained as invariants of the group of isometries of some homogeneous space.
Examples of non-Riemannian infinitesimal geometric structures include such structures as an absolute parallelism (field of frames), a conformal connection, a projective connection, a linear connection, a distribution (or, more generally, a flag structure), an almost-complex structure, an almost-symplectic structure, a field of affinors (cf. Affinor), etc. The geometry of these structures has been developed in analogy with Riemannian geometry. Its principal problems are: 1) To construct other structures derived from a given geometrical structure, in particular invariants — in other words, the construction of functors from a given category of geometric structures of a certain type into other categories. 2) A study of the group of automorphisms of a geometric structure, a study of geometric structures with a sufficiently large group of automorphisms, a description of the structures of a given type with a maximal group of automorphisms, and a classification of the structures of a given type on homogeneous spaces. 3) The equivalence problem, i.e. finding necessary and sufficient conditions for two geometrical structures to be equivalent. 4) The study of the relation between the topology and the structure of a smooth manifold on one hand, and the properties of the geometric structure defined on it, on the other. 5) A study of the mappings of manifolds with geometric structures, in particular of fibre bundles and submanifolds.
The most important class of geometric structures are transitive structures or  -structures [10]. All the examples of structures listed above (except for the field of affinors) are
-structures [10]. All the examples of structures listed above (except for the field of affinors) are 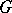 -structures. The general theory of
-structures. The general theory of 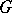 -structures is based on two fundamental ideas of Cartan: the concept of a prolongation and the concept of the structure function. In particular, in the case of a Riemannian metric these concepts lead to the Levi-Civita parallel displacement and the curvature tensor. The theory of
-structures is based on two fundamental ideas of Cartan: the concept of a prolongation and the concept of the structure function. In particular, in the case of a Riemannian metric these concepts lead to the Levi-Civita parallel displacement and the curvature tensor. The theory of 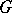 -structures of finite type is being developed, in many respects, similarly to Riemannian geometry. The best studied problems in the geometry of
-structures of finite type is being developed, in many respects, similarly to Riemannian geometry. The best studied problems in the geometry of 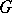 -structures of infinite type involve locally flat (integrable) structures, of which the most important ones are the complex structure (cf. Analytic manifold), the symplectic structure, which is the base of Hamiltonian mechanics, and the contact structure.
-structures of infinite type involve locally flat (integrable) structures, of which the most important ones are the complex structure (cf. Analytic manifold), the symplectic structure, which is the base of Hamiltonian mechanics, and the contact structure.
Cartan, who developed geometrical methods for solving systems of partial differential equations (Pfaffian systems), created the theory of exterior differential forms, which proved to be a major factor in the development of differential geometry [22]. The operator of exterior differentiation 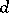 proved useful in expressing the integrability conditions of systems of partial differential equations. For instance, a necessary and sufficient condition for complete integrability of a Pfaffian system of equations
proved useful in expressing the integrability conditions of systems of partial differential equations. For instance, a necessary and sufficient condition for complete integrability of a Pfaffian system of equations 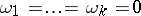 is that the ideal
is that the ideal 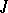 generated by the linear differential forms
generated by the linear differential forms  be closed with respect to
be closed with respect to 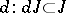 (the Frobenius theorem). The theory of differential forms was successfully employed by Cartan to solve various problems in differential geometry and the theory of Lie groups by the moving-frame method. The theory of integration establishes a connection between the calculus of differential forms and the homology of a manifold (cf. de Rham cohomology; Differential form).
(the Frobenius theorem). The theory of differential forms was successfully employed by Cartan to solve various problems in differential geometry and the theory of Lie groups by the moving-frame method. The theory of integration establishes a connection between the calculus of differential forms and the homology of a manifold (cf. de Rham cohomology; Differential form).
In a Riemannian space the operator of exterior differentiation 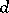 can be expressed in terms of the operator of covariant differentiation
can be expressed in terms of the operator of covariant differentiation  . Moreover, Hodge theory establishes an intimate connection between the operator
. Moreover, Hodge theory establishes an intimate connection between the operator 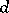 and the Laplace–Beltrami operator
and the Laplace–Beltrami operator 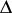 acting on the space of differential forms, which may be expressed in terms of the operator
acting on the space of differential forms, which may be expressed in terms of the operator  . Hodge's theorem states that the cohomology space of a compact manifold is isomorphic to the space of harmonic (i.e. annihilated by the operator
. Hodge's theorem states that the cohomology space of a compact manifold is isomorphic to the space of harmonic (i.e. annihilated by the operator 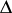 ) differential forms (cf. Harmonic form). This, and a number of other statements in Hodge theory, yields information about the structure of the cohomology ring
) differential forms (cf. Harmonic form). This, and a number of other statements in Hodge theory, yields information about the structure of the cohomology ring 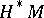 of a Riemannian space with non-trivial parallel differential forms (cf. Parallel field) and hence having a non-standard holonomy group
of a Riemannian space with non-trivial parallel differential forms (cf. Parallel field) and hence having a non-standard holonomy group 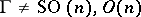 . Kähler manifolds and symmetric spaces are examples of such spaces (cf. Kähler manifold; Symmetric space).
. Kähler manifolds and symmetric spaces are examples of such spaces (cf. Kähler manifold; Symmetric space).
An important trend in studies of modern differential geometry is the study of natural vector bundles over an arbitrary manifold 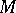 (tangent and cotangent bundles of order
(tangent and cotangent bundles of order 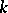 , tensor bundles, frame bundles of order
, tensor bundles, frame bundles of order 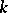 , jet bundles, etc.) and the discovery of their natural (i.e. invariant with respect to diffeomorphisms of the manifold
, jet bundles, etc.) and the discovery of their natural (i.e. invariant with respect to diffeomorphisms of the manifold 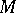 ) geometric structures [23]. Examples of such structures include the canonical symplectic structure in the cotangent bundle
) geometric structures [23]. Examples of such structures include the canonical symplectic structure in the cotangent bundle 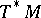 and the canonical contact structure in the bundle
and the canonical contact structure in the bundle 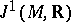 of
of 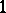 -jets of functions on
-jets of functions on 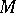 , which play an important role in the theory of partial differential equations of the first order and in Hamiltonian mechanics, as well as the operator of exterior differentiation in the bundle
, which play an important role in the theory of partial differential equations of the first order and in Hamiltonian mechanics, as well as the operator of exterior differentiation in the bundle 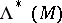 of exterior differential forms on
of exterior differential forms on 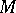 .
.
The algebraic approach to differential geometry is developing successfully. The initial concept here is not the manifold 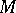 , but rather a commutative ring
, but rather a commutative ring 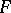 (the ring of functions on the manifold), while the manifold
(the ring of functions on the manifold), while the manifold 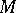 itself is defined in terms of
itself is defined in terms of 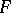 as the space of maximal ideals (cf. Scheme). Vector fields on
as the space of maximal ideals (cf. Scheme). Vector fields on 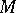 are defined as derivatives of this ring
are defined as derivatives of this ring 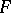 (cf. Derivation in a ring and Differential operator on a module). Such an approach makes it possible to generalize various results of differential geometry (e.g., to super-manifolds) and to simplify their proofs, to apply the ideas of differential geometry to other mathematical theories (e.g., to the theory of rings and modules) and, conversely, to use various algebraic results in differential geometry [17].
(cf. Derivation in a ring and Differential operator on a module). Such an approach makes it possible to generalize various results of differential geometry (e.g., to super-manifolds) and to simplify their proofs, to apply the ideas of differential geometry to other mathematical theories (e.g., to the theory of rings and modules) and, conversely, to use various algebraic results in differential geometry [17].
References
| [1] | B. Riemann, "Collected works" , Dover, reprint (1953) Zbl 0703.01020 Zbl 08.0231.03 |
| [2] | E. Cartan, "Leçons sur la géométrie des espaces de Riemann" , Gauthier-Villars (1928) MR1191392 MR0044878 MR0020842 MR1521868 Zbl 54.0755.01 |
| [3] | V.F. Kagan, , Outlines of geometry , Moscow (1963) pp. 437–519 (In Russian) |
| [4] | P.K. [P.K. Rashevskii] Rashewski, "Riemannsche Geometrie und Tensoranalyse" , Deutsch. Verlag Wissenschaft. (1959) (Translated from Russian) |
| [5] | V.I. Arnol'd, "Mathematical methods of classical mechanics" , Springer (1978) (Translated from Russian) Zbl 0692.70003 Zbl 0572.70001 Zbl 0647.70001 |
| [6] | L.P. Eisenhart, "Riemannian geometry" , Princeton Univ. Press (1949) MR0035081 Zbl 0041.29403 |
| [7] | S.W. Hawking, G.F.R. Ellis, "The large-scale structure of space-time" , Cambridge Univ. Press (1973) MR0424186 Zbl 0265.53054 |
| [8] | S. Helgason, "Differential geometry and symmetric spaces" , Acad. Press (1962) MR0145455 Zbl 0111.18101 |
| [9] | R.L. Bishop, R.J. Crittenden, "Geometry of manifolds" , Acad. Press (1964) MR0169148 Zbl 0132.16003 |
| [10] | S. Sternberg, "Lectures on differential geometry" , Prentice-Hall (1964) MR0193578 Zbl 0129.13102 |
| [11] | J.T. Schwartz, "Differential geometry and topology" , Gordon & Breach (1968) Zbl 0187.45006 |
| [12] | S. Lang, "Introduction to differentiable manifolds" , Interscience (1967) MR1931083 MR1532744 MR0155257 Zbl 1008.57001 Zbl 0103.15101 |
| [13] | R. Sulanke, P. Wintgen, "Differentialgeometrie und Faserbündel" , Deutsch. Verlag Wissenschaft. (1972) MR0413153 Zbl 0327.53020 Zbl 0271.53035 |
| [14] | R.O. Wells jr., "Differential analysis on complex manifolds" , Springer (1980) MR0608414 Zbl 0435.32004 |
| [15] | A. Lichnerowicz, "Géométrie des groupes de transformations" , Dunod (1958) MR0124009 Zbl 0096.16001 |
| [16] | S. Kobayashi, K. Nomizu, "Foundations of differential geometry" , 1–2 , Interscience (1963–1969) MR1393941 MR1393940 MR0238225 MR1533559 MR0152974 Zbl 0526.53001 Zbl 0508.53002 Zbl 0175.48504 Zbl 0119.37502 |
| [17] | I.S. Krasil'shchik, V.V. Lychagin, A.M. Vinogradov, "Geometry of jet spaces and nonlinear partial differential equations" , Gordon & Breach (1986) (Translated from Russian) MR861121 Zbl 0722.35001 |
| [18] | S.S. Chern, "Geometry of characteristic classes" Uspekhi Mat. Nauk , 33 : 3 (1973) pp. 15–111 (In Russian) MR0385881 Zbl 0292.57016 |
| [19] | S.A. Molchanov, "Diffusion processes and Riemannian geometry" Russian Math. Surveys , 30 : 1 (1975) pp. 1–63 Uspekhi Mat. Nauk , 30 : 1 (1975) pp. 3–59 Zbl 0315.53026 |
| [20] | J. Cheeger, D.G. Ebin, "Comparison theorems in Riemannian geometry" , North-Holland (1975) MR0458335 Zbl 0309.53035 |
| [21] | W. Greub, S. Halperin, R. Vanstone, "Connections, curvature, and cohomology" , 1–3 , Acad. Press (1972–1976) MR0400275 MR0336651 MR0336650 Zbl 0372.57001 Zbl 0335.57001 Zbl 0322.58001 |
| [22] | P. Flaschel, W. Klingenberg, "Riemannsche Hilbertmannigfaltigkeiten. Periodische Geodäten" , Lect. notes in math. , 282 , Springer (1972) MR0341527 |
| [23] | Ph.A. Griffiths, "Exterior differential systems and the calculus of variations" , Birkhäuser (1983) MR0684663 Zbl 0512.49003 |
| [24] | S. Kobayashi, "Transformation groups in differential geometry" , Springer (1972) MR0355886 Zbl 0246.53031 |
| [25] | A.L. Besse, "Einstein manifolds" , Springer (1987) MR0867684 Zbl 0613.53001 |
| [26] | A.L. Besse, "Géométrie Riemannienne en dimension 4" , F. Nathan (1981) MR0769127 |
Comments
For a modern version of Morse's theory see [a1]. For Riemann's course see also [a2]. References [a10]–[a13] are all general books on differentiable manifolds and applications.
References
| [a1] | W. Klingenberg, "Lectures on closed geodesics" , Springer (1968) MR0688143 MR0478069 MR0461361 Zbl 0517.58004 Zbl 0397.58018 |
| [a2] | B. Riemann, "Ueber die Hypothesen, welche der Geometrie zuGrunde liegen" , Das Kontinuum und andere Monographien , Chelsea, reprint (1973) Zbl 0093.00101 Zbl 0087.35001 Zbl 47.0518.05 |
| [a3] | H. Rund, "The differential geometry of Finsler spaces" , Springer (1959) MR0105726 Zbl 0087.36604 |
| [a4] | E. Cartan, "Les systèmes différentielles extérieurs et leur applications géométriques" , Hermann (1971) |
| [a5] | P.A. Griffith, G.R. Jensen, "Differential systems and isometric embeddings" , Princeton Univ. Press (1987) |
| [a6] | H. Flanders, "Differential forms with applications to the physical sciences" , Acad. Press (1963) MR0162198 Zbl 0112.32003 |
| [a7] | E. Kähler, "Einführung in die Theorie der Systeme von Differentialgleichungen" , Chelsea, reprint (1949) Zbl 0011.16103 Zbl 60.0401.08 |
| [a8] | E. Cartan, "La théorie des groupes finis et continus et la géométrie différentielle traitées par la méthode du repère mobile" , Gauthier-Villars (1937) MR1190006 Zbl 0018.29804 Zbl 63.1227.02 |
| [a9] | J.W. Milnor, J.D. Stasheff, "Characteristic classes" , Princeton Univ. Press (1974) MR0440554 Zbl 0298.57008 |
| [a10] | G. de Rham, "Differentiable manifolds" , Springer (1984) (Translated from French) Zbl 0534.58003 |
| [a11] | W.M. Boothby, "An introduction to differentiable manifolds and Riemannian geometry" , Acad. Press (1975) MR0426007 Zbl 0333.53001 |
| [a12] | C. DeWitt-Murette, "Analysis, manifolds and physics" , North-Holland (1982) (Translated from French) |
| [a13] | J. Dieudonne, "Treatise on analysis" , 4 , Acad. Press (1974) MR0362066 Zbl 0292.58001 |
Differential geometry of manifolds. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Differential_geometry_of_manifolds&oldid=24418