Chern class
A characteristic class defined for complex vector bundles. A Chern class of the complex vector bundle 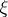 over a base
over a base  is denoted by
is denoted by 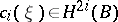 and is defined for all natural indices
and is defined for all natural indices 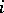 . By the complete Chern class is meant the inhomogeneous characteristic class
. By the complete Chern class is meant the inhomogeneous characteristic class 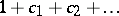 , and the Chern polynomial is the expression
, and the Chern polynomial is the expression 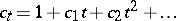 , where
, where 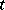 is a formal unknown. Chern classes were introduced in [1].
is a formal unknown. Chern classes were introduced in [1].
The characteristic classes, defined for all  -dimensional complex vector bundles and with values in the integral cohomology, are naturally identified with the elements of the ring
-dimensional complex vector bundles and with values in the integral cohomology, are naturally identified with the elements of the ring 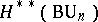 . In this sense the Chern classes
. In this sense the Chern classes 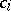 can be thought of as elements of the groups
can be thought of as elements of the groups 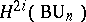 , the complete Chern class as an element of the ring
, the complete Chern class as an element of the ring 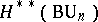 , and the Chern polynomial as an element of the formal power series ring
, and the Chern polynomial as an element of the formal power series ring 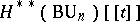 .
.
The Chern classes satisfy the following properties, which uniquely determine them. 1) For two vector bundles 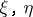 with a common base
with a common base 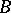 ,
,  , in other words
, in other words 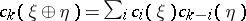 where
where  . 2) For the one-dimensional universal bundle
. 2) For the one-dimensional universal bundle 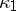 over
over 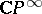 the identity
the identity 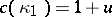 holds, where
holds, where 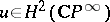 is the orientation of
is the orientation of 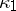 (
(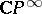 is the Thom space of
is the Thom space of 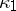 , which, being complex, has a uniquely-defined orientation
, which, being complex, has a uniquely-defined orientation  ).
).
Consequences of the properties 1)–2) are: 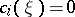 for
for 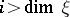 , and
, and 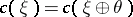 , where
, where 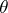 is the trivial bundle. The latter fact allows one to define Chern classes as elements of the ring
is the trivial bundle. The latter fact allows one to define Chern classes as elements of the ring 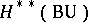 .
.
If 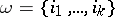 is a collection of non-negative integers, then
is a collection of non-negative integers, then 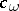 denotes the characteristic class
denotes the characteristic class 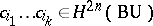 , where
, where 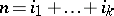 .
.
Under the natural monomorphism 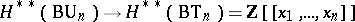 induced by the mapping
induced by the mapping 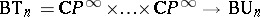 , the Chern classes are mapped into the elementary symmetric functions, and the complete Chern class is mapped to the polynomial
, the Chern classes are mapped into the elementary symmetric functions, and the complete Chern class is mapped to the polynomial 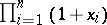 . The image of the ring
. The image of the ring  in
in 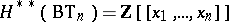 is the subring consisting of all symmetric formal power series. Every symmetric formal power series in the Wu generators
is the subring consisting of all symmetric formal power series. Every symmetric formal power series in the Wu generators  determines a characteristic class that can be expressed in terms of Chern classes. For example, the series
determines a characteristic class that can be expressed in terms of Chern classes. For example, the series 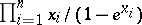 determines a characteristic class with rational coefficients, called the Todd class and denoted by
determines a characteristic class with rational coefficients, called the Todd class and denoted by 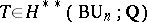 .
.
Let 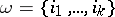 be a set of non-negative integers. Let
be a set of non-negative integers. Let 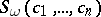 denote the characteristic class defined by the smallest symmetric polynomial in the variables
denote the characteristic class defined by the smallest symmetric polynomial in the variables  , where
, where  , containing the monomial
, containing the monomial 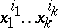 .
.
Let  be an oriented multiplicative cohomology theory. Then the Chern classes
be an oriented multiplicative cohomology theory. Then the Chern classes 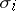 with values in
with values in 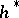 satisfy, as do ordinary Chern classes, the properties:
satisfy, as do ordinary Chern classes, the properties: 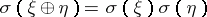 ,
,  ,
, 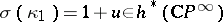 , where
, where 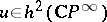 is the orientation of the bundle
is the orientation of the bundle 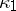 , and these properties completely determine them. As with ordinary Chern classes, one uses the notation
, and these properties completely determine them. As with ordinary Chern classes, one uses the notation 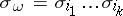 and
and 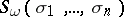 . If
. If 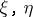 are two complex vector bundles, then
are two complex vector bundles, then
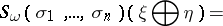 |
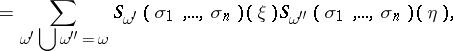 |
where the summation is taken over all sets 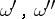 with
with 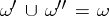 .
.
In place of the theory 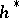 one may take a unitary cobordism theory
one may take a unitary cobordism theory 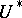 or
or 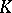 -theory. For a
-theory. For a 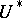 -theory the element
-theory the element 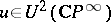 is defined by the identity mapping
is defined by the identity mapping 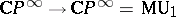 , and for
, and for 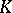 -theory
-theory 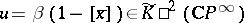 , where
, where 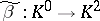 is the Bott periodicity operator. The notation
is the Bott periodicity operator. The notation 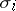 is retained for Chern classes with values in a
is retained for Chern classes with values in a 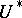 -theory, while Chern classes with values in
-theory, while Chern classes with values in 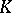 -theory are denoted by
-theory are denoted by 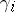 .
.
According to the general theory, 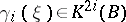 , where
, where 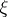 is a vector bundle with base
is a vector bundle with base 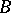 . However
. However 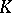 -theory is often conveniently thought of as a
-theory is often conveniently thought of as a  -graded theory, identifying the groups
-graded theory, identifying the groups 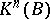 and
and 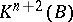 via the periodicity operator
via the periodicity operator 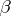 . Then
. Then 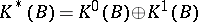 and
and 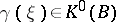 for all
for all 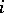 . From this point of view it makes sense to consider, instead of the complete Chern class, the Chern polynomial
. From this point of view it makes sense to consider, instead of the complete Chern class, the Chern polynomial
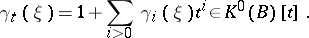 |
Let 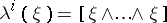 be a cohomology operation in
be a cohomology operation in 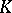 -theory (
-theory (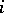 terms). The polynomial
terms). The polynomial
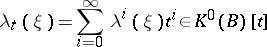 |
satisfies, as does 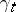 , the multiplicative property
, the multiplicative property
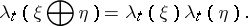 |
There is the following connection between these polynomials:
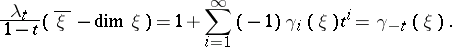 |
Here both parts of the equation lie in 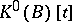 and
and 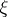 is the trivial bundle of dimension
is the trivial bundle of dimension 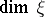 . The classes
. The classes 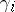 in this construction are different from those constructed by M.F. Atiyah, who defined them by the formula
in this construction are different from those constructed by M.F. Atiyah, who defined them by the formula 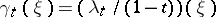 . R. Stong [2] defined classes
. R. Stong [2] defined classes 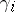 that satisfy the condition
that satisfy the condition
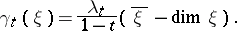 |
The difference arises because, for Stong,
 |
The classes 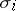 are connected with the notion of a Landweber–Novikov algebra, which is very fruitful in homotopy theory. For an arbitrary set
are connected with the notion of a Landweber–Novikov algebra, which is very fruitful in homotopy theory. For an arbitrary set 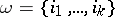 of non-negative integers, consider the characteristic class
of non-negative integers, consider the characteristic class 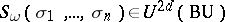 , where
, where 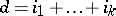 . There is a Thom isomorphism
. There is a Thom isomorphism 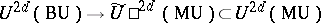 , where
, where 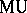 is the spectrum corresponding to the
is the spectrum corresponding to the 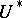 -theory. The image of the class
-theory. The image of the class 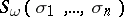 in
in 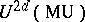 determines a cohomology operation in the
determines a cohomology operation in the 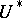 -theory. The subalgebra of the Steenrod algebra in the
-theory. The subalgebra of the Steenrod algebra in the 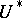 -theory generated by the operations of this form is called the Landweber–Novikov algebra. The operation constructed from the set
-theory generated by the operations of this form is called the Landweber–Novikov algebra. The operation constructed from the set 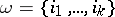 is denoted by
is denoted by 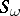 .
.
For one-dimensional bundles 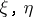 there is the identity
there is the identity
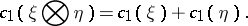 |
This important property, which enables one to define the Chern character, does not hold in generalized cohomology theories. However there exists a formal power series 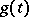 with coefficients in
with coefficients in 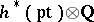 , such that
, such that 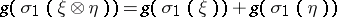 , where
, where 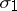 is the first Chern class with coefficients in
is the first Chern class with coefficients in 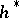 . For the unitary cobordism theory
. For the unitary cobordism theory
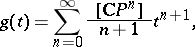 |
where 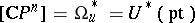 is the cobordism class of the projective space
is the cobordism class of the projective space 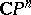 . This series is called the Mishchenko series.
. This series is called the Mishchenko series.
References
| [1] | S.S. Chern, "Characteristic classes of Hermitian manifolds" Ann. of Math. , 47 : 1 (1946) pp. 85–121 |
| [2] | R.E. Stong, "Notes on cobordism theory" , Princeton Univ. Press (1968) |
| [3] | R.S. Palais, "Seminar on the Atiyah–Singer index theorem" , Princeton Univ. Press (1965) |
| [4] | P.E. Conner, E.E. Floyd, "Differentiable periodic maps" , Springer (1964) |
| [5a] | M.F. Atiyah, I.M. Singer, "The index of elliptic operators I" Ann. of Math. (2) , 87 (1968) pp. 484–530 |
| [5b] | M.F. Atiyah, G.B. Segal, "The index of elliptic operators II" Ann. of Math. (2) , 87 (1968) pp. 531–545 |
| [5c] | M.F. Atiyah, I.M. Singer, "The index of elliptic operators III" Ann. of Math. (2) , 87 (1968) pp. 546–604 |
| [5d] | M.F. Atiyah, I.M. Singer, "The index of elliptic operators IV" Ann. of Math. (2) , 93 (1971) pp. 119–138 |
| [5e] | M.F. Atiyah, I.M. Singer, "The index of elliptic operators V" Ann. of Math. (2) , 93 (1971) pp. 139–149 |
| [6] | F. Hirzebruch, "Topological methods in algebraic geometry" , Springer (1978) (Translated from German) |
| [7] | D. Husemoller, "Fibre bundles" , McGraw-Hill (1966) |
| [8] | V.M. Bukhshtaber, "The Chern–Dold character in cobordisms" Math. USSR-Sb. , 12 : 4 (1970) pp. 573–594 Mat. Sb. , 83 (1970) pp. 575–595 |
| [9] | S.P. Novikov, "The method of algebraic topology from the viewpoint of cobordism theory" Math. USSR-Izv. , 4 : 1 (1967) pp. 827–913 Izv. Akad. SSSR Ser. Mat. , 31 : 4 (1967) pp. 855–951 |
| [10] | M.F. Atiyah, "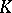 -theory: lectures" , Benjamin (1967) -theory: lectures" , Benjamin (1967) |
Comments
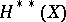 denotes the completion
denotes the completion 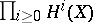 of
of 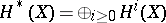 .
.
The power series 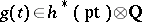 for a complex oriented cohomology theory
for a complex oriented cohomology theory 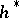 such that
such that 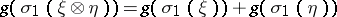 is the logarithm of the formal group
is the logarithm of the formal group 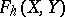 defined by
defined by 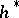 ; cf. Cobordism and Formal group for some more details.
; cf. Cobordism and Formal group for some more details.
Chern class. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Chern_class&oldid=15158