Integral exponential function

The special function defined for real $x \neq 0$ by the equation

$$\mathop{\rm Ei} ( x) = \ \int\limits _ {- \infty } ^ { x } \frac{e ^ {t} }{t} d t = - \int\limits _ { - x} ^ \infty \frac{e ^ {-} t }{t} d t .$$

The graph of the integral exponential function is illustrated in Fig..

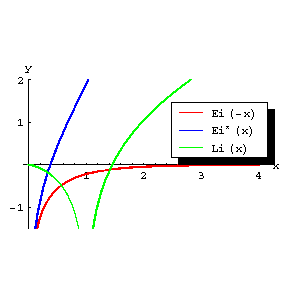
Figure: i051440a

Graphs of the functions $y = \mathop{\rm Ei} ( - x )$, $y = \mathop{\rm Ei} ^ {*} ( x)$ and $y = \mathop{\rm Li} ( x)$.

For $x > 0$, the function $e ^ {t} / t$ has an infinite discontinuity at $t = 0$, and the integral exponential function is understood in the sense of the principal value of this integral:

$$\mathop{\rm Ei} ( x) = \ \lim\limits _ {\epsilon \rightarrow + 0 } \ \left \{ \int\limits _ {- \infty } ^ \epsilon \frac{e ^ {t} }{t} d t + \int\limits _ \epsilon ^ { x } \frac{e ^ {t} }{t} d t \right \} .$$

The integral exponential function can be represented by the series

$$\tag{1 } \mathop{\rm Ei} ( x) = \ c + \mathop{\rm ln} ( - x ) + \sum _ { k= } 1 ^ \infty \frac{x ^ {k} }{k!k} ,\ \ x < 0 ,$$

and

$$\tag{2 } \mathop{\rm Ei} ( x) = c + \mathop{\rm ln} ( x) + \sum _ { k= } 1 ^ \infty \frac{x ^ {k} }{k!k} ,\ \ x > 0 ,$$

where $c = 0.5772 \dots$ is the Euler constant.

There is an asymptotic representation:

$$\mathop{\rm Ei} ( - x ) \approx \ \frac{e ^ {-} x }{x} \left ( 1 - 1! over {x} + 2! over {x ^ {2} } - 3! over {x ^ {3} } + \dots \right ) ,\ \ x \rightarrow + \infty .$$

As a function of the complex variable $z$, the integral exponential function

$$\mathop{\rm Ei} ( z) = \ C + \mathop{\rm ln} ( - z ) + \sum _ { k= } 1 ^ \infty \frac{z ^ {k} }{k!k} ,\ \ | \mathop{\rm arg} ( - z ) | < \pi ,$$

is a single-valued analytic function in the $z$- plane slit along the positive real semi-axis $( 0 < \mathop{\rm arg} z < 2 \pi )$; here the value of $\mathop{\rm ln} ( - z)$ is chosen such that $- \pi < { \mathop{\rm Im} \mathop{\rm ln} } (- z) < \pi$. The behaviour of $\mathop{\rm Ei} ( z)$ close to the slit is described by the limiting relations:

$$\left . \begin{array}{c} \lim\limits _ {\eta \downarrow 0 } \ \mathop{\rm Ei} ( z + i \eta ) = \ \mathop{\rm Ei} ( z) - i \pi , \\ \lim\limits _ {\eta \downarrow 0 } \ \mathop{\rm Ei} ( z - i \eta ) = \ \mathop{\rm Ei} ( z) + i \pi , \\ \end{array} \right \} \ \ z = x + i y.$$

The asymptotic representation in the region $0 < \mathop{\rm arg} z < 2 \pi$ is:

$$\mathop{\rm Ei} ( z) \sim \ \frac{e ^ {z} }{z} \left ( 1! over {z} + 2! over {z ^ {2} } + \dots + k! over {z ^ {k} } + \dots \right ) ,\ \ | z | \rightarrow \infty .$$

The integral exponential function is related to the integral logarithm $\mathop{\rm li} ( x)$ by the formulas

$$\mathop{\rm Ei} ( x) = \ \mathop{\rm li} ( e ^ {x} ) ,\ \ x < 0 ,$$

$$\mathop{\rm Ei} ( \mathop{\rm ln} x ) = \mathop{\rm li} ( x) ,\ x < 1 ;$$

and to the integral sine $\mathop{\rm Si} ( x)$ and the integral cosine $\mathop{\rm Ci} ( x)$ by the formulas:

$$\mathop{\rm Ei} ( \pm i x ) = \ \mathop{\rm Ci} ( x) \pm i \mathop{\rm Si} ( x) \mps \frac{\pi i }{2} ,\ \ x > 0 .$$

The differentiation formula is:

$$\frac{d ^ {n} \mathop{\rm Ei} ( - x ) }{d x ^ {n} } = \ ( - 1 ) ^ {n-} 1 ( n - 1 ) ! x ^ {-} x e ^ {-} x e _ {n-} 1 ( x) ,\ \ n = 1 , 2 , . . . .$$

The following notations are sometimes used:

$$\mathop{\rm Ei} ^ {+} ( z) = \ \mathop{\rm Ei} ( z + i 0 ) ,\ \ \mathop{\rm Ei} ^ {-} ( z) = \ \mathop{\rm Ei} ( z - i 0 ) ,$$

$$\mathop{\rm Ei} ^ {*} ( z) = { \mathop{\rm Ei} ( z) } bar = \mathop{\rm Ei} ( z) + \pi i .$$

References

[1]	H. Bateman (ed.) A. Erdélyi (ed.) et al. (ed.) , Higher transcendental functions , 2. Bessel functions, parabolic cylinder functions, orthogonal polynomials , McGraw-Hill (1953)
[2]	E. Jahnke, F. Emde, "Tables of functions with formulae and curves" , Dover, reprint (1945) (Translated from German)
[3]	A. Krazer, W. Franz, "Transzendente Funktionen" , Akademie Verlag (1960)
[4]	N.N. Lebedev, "Special functions and their applications" , Prentice-Hall (1965) (Translated from Russian)

Comments

The function $\mathop{\rm Ei}$ is usually called the exponential integral.

Instead of by the series representation, for complex values of $z$( $x$ not positive real) the function $\mathop{\rm Ei} ( z)$ can be defined by the integal (as for real $x \neq 0$); since the integrand is analytic, the integral is path-independent in $\mathbf C \setminus \{ {x \in \mathbf R } : {x \geq 0 } \}$.

Formula (1) with $x$ replaced by $z$ then holds for $| \mathop{\rm arg} ( - z ) | < \pi$, and the function defined by (2) (for $x > 0$) is also known as the modified exponential integral.