Howell design
A Howell design of side $ s $
and order $ 2n $,
or more briefly an $ H ( s,2n ) $,
is an $ ( s \times s ) $-
array in which each cell is either empty or contains an unordered pair of distinct elements from some $ 2n $-
set $ V $
such that:
1) every element of $ V $ occurs in precisely one cell of each row and each column;
2) every unordered pair of elements from $ V $ is in at most one cell of the array. It follows immediately from the definition of an $ H ( s,2n ) $ that $ n \leq s \leq 2n - 1 $. An example of a Howell design is the following $ H ( 4,6 ) $:
<tbody> </tbody>
|
An $ H ( 2n - 1,2n ) $ is also called a Room square of side $ 2n - 1 $. At the other extreme, the existence of a pair of mutually orthogonal Latin squares implies the existence of an $ H ( n,2n ) $. The existence of Howell designs has been completely determined [a1], [a5]: Let $ s $ and $ n $ be positive integers such that $ 0 \leq n \leq s \leq 2n - 1 $. There exists an $ H ( s,2n ) $ if and only if $ ( s,2n ) \neq ( 2,4 ) , ( 3,4 ) , ( 5,6 ) $ or $ ( 5,8 ) $. The proof uses a variety of direct and recursive constructions.
An $ H ^ {*} ( s,2n ) $ is an $ H ( s,2n ) $ in which there is a subset $ W $ of $ V $, $ | W | = 2n - s $, such that no pair of elements from $ W $ appears in the design. $ * $- designs are quite useful in recursive constructions. There exist $ H ^ {*} ( s,2n ) $ for $ s $ even, $ n \leq s \leq 2n - 2 $, with two exceptions: there is no $ H ^ {*} ( 2,4 ) $ and there is no $ H ^ {*} ( 6,12 ) $[a1]. The existence of $ H ^ {*} ( s,2n ) $ for $ s $ odd remains open, see [a5]. The only known case where an $ H ( s,2n ) $ exists but an $ H ^ {*} ( s,2n ) $ does not is for $ s = n = 6 $.
The pairs of elements in the cells of an $ H ( s,2n ) $ can be thought of as the edges of an $ s $- regular graph on the $ 2n $- set $ V $, the underlying graph of the Howell design. The existence of an $ H ( s,2n ) $ is equivalent to the existence of a pair of orthogonal one-factorizations of the underlying graph of the $ H ( s,2n ) $( cf. One-factorization). The underlying graph of an $ H ( 2n - 1,2n ) $ is the complete graph $ K _ {2n } $, and the underlying graph of an $ H ( 2n - 2,2n ) $ is the cocktail party graph $ K _ {2n } - f $, where $ f $ is a one-factor. An $ H ( n,2n ) $ with underlying graph $ K _ {n,n } $ is equivalent to a pair of mutually orthogonal Latin squares of order $ n $. The general problem of determining which graphs are the underlying graphs of a Howell design remains open (1996), see [a3].
Several special types of Howell designs have been studied, including $ ** $- designs, skew designs, complementary designs, $ * $- complementary designs, cyclic Howell designs (used for Howell movements in duplicate bridge), and Howell designs with Howell sub-designs (see [a3] [a4]).
A $ d $- dimensional Howell design, $ H _ {d} ( s,2n ) $, is a $ d $- dimensional array in which every cell either is empty or contains an unordered pair of elements from a $ 2n $- set $ V $ and such that each two-dimensional projection is an $ H ( s,2n ) $. An $ H _ {3} ( s,2n ) $ is called a Howell cube. An $ H _ {d} ( s,2n ) $ is equivalent to $ d $ mutually orthogonal one-factorizations of the underlying graph. Let $ \nu ( s,2n ) $ denote the maximum value of $ d $ such that an $ H _ {d} ( s,2n ) $ exists. Very little is known about upper bounds for $ \nu ( s,2n ) $. It is easy to see that $ \nu ( s,2n ) \leq s - 1 $, and it has been conjectured that $ \nu ( s,2n ) \leq n - 1 $. See [a3], [a2] for results on $ \nu ( s,2n ) $ and existence results on $ H _ {d} ( s,2n ) $.
The survey article [a3] includes results and references on Howell designs.
References
| [a1] | B.A. Anderson, P.J. Schellenberg, D.R. Stinson, "The existence of Howell designs of even side" J. Combin. Th. A , 36 (1984) pp. 23–55 |
| [a2] | J.H. Dinitz, "Howell designs" C.J. Colbourn (ed.) J.H. Dinitz (ed.) , CRC Handbook of Combinatorial Designs , CRC (1996) pp. 381–385 |
| [a3] | J.H. Dinitz, D.R. Stinson, "Room squares and related designs" J.H. Dinitz (ed.) D.R. Stinson (ed.) , Contemporary Design Theory: A Collection of Surveys , Wiley (1992) pp. 137–204 |
| [a4] | E.R. Lamken, S.A. Vanstone, "The existence of skew Howell designs of side 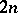 and order and order 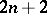 " J. Combin. Th. A , 54 (1990) pp. 20–40 " J. Combin. Th. A , 54 (1990) pp. 20–40 |
| [a5] | D.R. Stinson, "The existence of Howell designs of odd side" J. Combin. Th. A , 32 (1982) pp. 53–65 |
Howell design. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Howell_design&oldid=47277